 |
Правило, выраженное приведенным ниже утверждением.
|
|
|
|
Утверждение 12.11. Для / = 1, …, п в диграфе Gk тогда и только тогда имеется путь (v,,vy), когда в диграфе существует направленный путь от v, до Vj, если расположенные между ними узлы (при наличии таковых) будут входить в множество {vi, v^}. В частности, Gn равен G\ транзитивному замыканию диграфа G.
Из утверждения 12.11 вытекает простой алгоритм вычисления транзитивного замыкания диграфа <5, в основу которого положена серия описанных выше циклов. Данный алгоритм получил известность как алгоритм Флойда-Уоршалла, и его псевдокод приведен во фрагменте кода 12.10. С помощью этого псевдокода легко проанализировать время выполнения алгоритма Флойда-Уоршалла, поскольку структура данных, представляющая G, поддерживает выполнение методов areAdjacent и insertDirectedEdge за 0(1) времени. Основной цикл выполняется п раз, а внутренний цикл обрабатывает каждую из 0(п2) пар узлов, выполняя для каждой пары вычислительные операции с постоянным временем. Таким образом, общее время выполнения алгоритма Флойда-Уоршалла составляет 0(я3).
Алгоритм FloydWarshall(G):
Input: диграф G из п узлов.
Output: транзитивное замыкание G* диграфа G.
Пусть vb v2, vn будет произвольной нумерацией узлов диграфа G, Go <~ G
for к <- 1 to п do
Gk G k_i
for каждого /’, у в {1, п} при / * j и /, ] * к do if узлы (vit vk) и (vk, vj) входят в Gk_^ then
добавить узел (vh vj) к Gk (если такого еще нет)
return Gn
Фрагмент кода 12.10. Псевдокод алгоритма Флойда-Уоршалла. Алгоритм вычисляет транзитивное замыкание G* диграфа G, вычисляя по возрастающей серию диграфов G0, Gv Gn, где k = 1, …, п
Это описание является всего лишь примером алгоритмической проектной модели, известной как динамическое программирование (см. п. 11.5.2). Из этого описания и анализа следует нижеприведенное утверждение.
|
|
|
Утверждение 12.12. Пусть G будет диграфом из п узлов и представлен структурой данных, поддерживающей поиск и обновление информации списка смежности за 0(1) времени. Тогда алгоритм Флойда-Уоршалла вычисляет транзитивное замыкание G* диграфа G за 0(п 3) времени.
Пример выполнения алгоритма Флойда-Уоршалла приведен на рис. 12.10.

Рис. 12.10. Последовательность диграфов, вычисляемых алгоритмом Флойда-Уоршалла: (а) исходный диграф G = G0 и нумерация узлов; (Ь) диграф <5,; (с) G2\ (d) G3; (е) G4; (0 Gs. Заметьте, что G5 = G6 =Gr Поскольку в ди- графе Gk_{ имеются пути (v^v^) и (v^vy), но отсутствует путь (v/,vy-), то на рисунке пути и (v^vj) показаны линиями с точечным штри-
\ > хбм, а путь (vi,vj) — линией с длинным штрихом
Производительность алгоритма Флойда-Уоршалла
\ *
Время выполнения алгоритма Флойда-Уоршалла может оказаться большим, чем время DFS из каждого узла направленного графа, но оно будет зависеть от типа структуры, используемой для представления графа. Если граф представлен матрицей смежности, то выполнение DFS-ме- тода в направленном графе G займет 0(п 2) времени. Таким образом, выполнение DFS п раз занимает 0{пг) времени, что ничем не лучше разового выполнения алгоритма Флойда-Уоршалла. Если же граф представлен структурой списка смежности, то для вычисления транзитивного замыкания выполнение DFS-алгоритма п раз займет 0(п(п + т)) времени. Но даже в этом случае, если граф будет насыщенным, то есть имеет 0(я2) пу-;тей, то все равно потребуется 0{пг) времени, причем гораздо сложнее разового применения алгоритма Флойда-Уоршалла. Единственным случаем, когда повторное обращение к DFS-методу предпочтительнее, является ненасыщенный граф, представленный структурой списка смежности.
8. Поиск кротчайшего пути (алгоритмы)
Алгоритм поиска кратчайшего пути
Результатом алгоритма поиска кратчайшего пути является последовательность ребер, соединяющая заданные две вершины и имеющая наименьшую длину среди всех таких последовательностей.
На первый взгляд кажется, что мы можем воспользоваться алгоритмом построения МОД, чтобы отбросить лишние ребра, а затем взять путь, соединяющий заданные вершины в построенном остовном дереве. К сожалению, такие действия не всегда приводят к нужному результату.
Напомним, что алгоритм построения МОД нацелен на поиск дерева с минимальным суммарным весом ребер. Рассмотрим, например, "циклический" граф, то есть такой граф, в котором первая вершина соединена со второй, вторая - с третьей, и так далее, а последняя вершина в свою очередь соединена с первой. Такой граф представляет собой просто кольцо, каждая вершина в котором соединена с двумя другими. Пример такого графа с шестью вершинами приведен на рис. 1 (а).
|
|
|
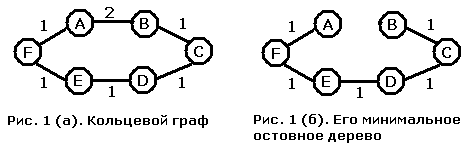
Обратите внимание на то, что вес каждого ребра равен 1 за исключением ребра, соединяющего вершины A и B, вес которого равен 2. Алгоритм построения минимального остовного дерева выберет все ребра веса 1, отбросив единственное ребро веса 2. Это означает, однако, что путь от A к B в минимальном остовном дереве должен проходить через все остальные вершины, а его длина равна 5 (рис. 1 (б)). Ясно, что он не является кратчайшим, поскольку в исходном графе вершины A и B соединены ребром длины 2.
Алгоритм Дейкстры
Жадный алгоритм построения минимального остовного дерева непригоден для поиска кратчайшего пути между двумя вершинами, поскольку на каждом проходе он учитывает длину лишь одного ребра. Если же изменить его так, чтобы при выборе ребра, ведущего в кайму, он выбирал ребро, являющееся частью кратчайшего пути в целом пути из начальной вершины, то мы получим требуемый результат. Точнее говоря, вот измененный алгоритм:
выбрать начальную вершину
создать начальную кайму из вершин, соединенных с начальной
while вершина назначения не достигнута do
выбрать вершину каймы с кратчайшим расстоянием до начальной
добавить эту вершину и ведущее в нее ребро к дереву
изменить кайму путем добавления к ней вершин,
соединенных с вновь добавленной
for всякой вершины каймы do
приписать к ней ребро, соединяющее ее с деревом и
завершающее кратчайший путь к начальной вершине
|
|
|
End for
End while
На рис. 2 приведен пример исполнения этого алгоритма. Алгоритм выполняется на том же графе (рис. 2 (а)), что и алгоритм построения минимального остовного дерева, а искать мы будем кратчайший путь от A до G.
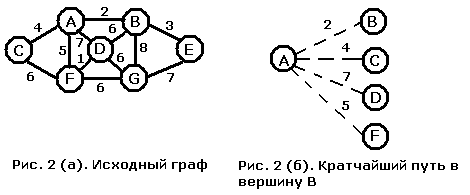
В начале пути из вершины A у нас есть четыре возможных ребра. Из этих четырех ребер ребро AB является кратчайшим. Поэтому мы добавляем к дереву вершину B (рис. 2 (в)) и смотрим, как следует обновить набор путей. С уже построенным деревом соединены теперь вершины E и G, поэтому их следует добавить к кайме. Кроме того, мы должны посмотреть на вершину D и сравнить прямой путь из нее в A, длина которого равна 7, с окольным путем через вершину B, длина которого равна 8. Прямой путь короче, поэтому приписанное к D ребро менять не следует. Изучив теперь имеющиеся возможности, мы видим, что кратчайшим является путь из A в C длины 4. Ребро BE короче, однако, мы рассматриваем полную длину пути из A, а такой путь, ведущий в E, имеет длину 5. Теперь к дереву кратчайших путей добавим вершину C (рис. 2 (г)). Посмотрев на граф, мы обнаруживаем, что можем пройти в вершину F через вершину C, однако длина этого пути будет равна 10 - больше, чем у прямого пути из A в F, поэтому изменения в наборе путей не производится.
На рис. 2 (г) мы можем выбрать теперь либо путь из A в F, либо путь из A в E, проходящий через вершину B: оба они имеют длину 5. Какой из путей будет выбран при исполнении программы, зависит от способа хранения данных в ней. Мы же, встретившись с необходимостью добавить вершину, будем всегда выбирать вершину, метка которой первая в лексикографическом порядке.

В результате получим ситуацию с рис. 2 (д). Добавление к дереву вершины E не меняет остальных связей, поэтому теперь мы можем добавить вершину F и получим картинку с рис. 2 (е). Обратите внимание на то, что, хотя добавление вершины F и привело к изменению ребра, ведущего из D, если бы мы начали с F, все равно на очередном шаге мы должны были бы добавить E.
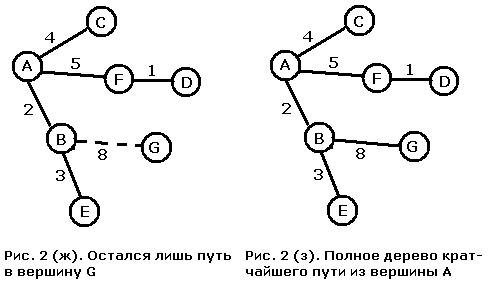
На рис. 2 (е) видно, что путь в вершину D короче пути в вершину G. Поэтому мы добавляем к дереву вершину D и получаем ситуацию, изображенную на рис. 2 (ж). Осталось добавить только вершину G, и в результате мы получаем дерево кратчайшего пути с рис. 2 (з). Длина кратчайшего пути из A в G равна 10.
|
|
|

На примере с рис. 2 мы имеем дело с полным деревом кратчайших путей, поскольку целевая вершина G была добавлена к дереву последней. Если бы мы добрались до нее раньше, алгоритм бы тотчас завершил свою работу. Могут возникнуть ситуации, в которых нас интересуют кратчайшие пути из данной вершины во все остальные. Если, например, мы имеем дело с небольшой компьютерной сетью, скорости передачи данных между узлами которой приблизительно постоянны, то для каждого из компьютеров сети мы можем выбрать кратчайший путь до каждого из остальных компьютеров. Поэтому при необходимости переслать сообщение единственное, что нам потребуется, это воспользоваться заранее рассчитанным наиболее эффективным путем.
9. Дерево. (свойства)
В теории графов, дерево — связный (ориентированный или неориентированный) граф, не содержащий циклов (для любой вершины есть один и только один способ добраться до любой другой вершины). Древовидная структура — тип организации, в котором каждый объект связан с хотя бы одним другим.
Свойства дерева
· Дерево не имеет кратных ребер и петель.
· Любое дерево с n вершинами содержит n − 1 ребро. Более того, конечный связный граф является деревом тогда и только тогда, когда B − P = 1, здесь B — число вершин, P — число рёбер графа.
· Граф является деревом тогда и только тогда, когда любые две различные его вершины можно соединить единственным элементарным путём.
· Любое дерево однозначно определяется расстояниями (длиной наименьшей цепи) между его концевыми (степени 1) вершинами.
· Любое дерево является двудольным графом. Любое дерево, содержащее счётное количество вершин, является планарным графом.
10. Цикломатическое число.
ЦИКЛОМАТИЧЕСКОЕ ЧИСЛО [cyclomatic number] — термин теории графов: одна из возможных числовых характеристик несвязного графа. Если граф X имеет n вершин, m ребер, а p — количество его связных частей, компонент (см. Граф), то Ц. ч. определяется равенством
v(X) = m – n + p.
При Ц. ч., равном нулю, граф не содержит циклов; если же оно равно единице, то граф имеет только один цикл.
11. Критический путь в сетевом графике (алгоритм)
Путь максимальной длины есть смысл искать только в графах, где нет контуров. Действительно, в графе с контурами решение однозначно и равно бесконечности, ибо существует путь, бесконечное число раз проходящий по этому контуру. Одной из задач, где используется поиск максимального пути, является задача анализа сетевого графика. Дадим необходимые определения.
|
|
|
Семантика задачи. Сопоставим каждой дуге работу. Вес дуги - время выполнения работы.
Вершине сопоставим событие, состоящее в том, что все работы, приписанные заходящим в нее дугам, выполнены, и можно начинать все работы, приписанные исходящим дугам. Граф с такой трактовкой называется диаграммой ПЕРТ (от Program Evaluation and Review Technique) или сетевым графиком.
В сетевом графике максимальному пути, называемому критическим, будет соответствовать минимальное время, необходимое для выполнения всех работ. Для сокращения общего времени можно рассматривать, например, вопрос об автоматизации работ на критическом пути с целью сокращения времени их выполнения.
Для решения задачи поиска максимального пути можно воспользоваться алгоритмом Дейкстры, изменив его соответствующим образом.
Однако задано добавочное условие на граф задачи: в нем нет контуров.
Добавочные условия могут потребовать проверки их выполнения и усложнить алгоритм, но можно использовать эти условия и для сокращения алгоритма, что мы и сделаем.
Справедлива следующая теорема: если в графе нет контуров, то его вершины можно перенумеровать таким образом, что всякая дуга идет из вершины с меньшим номером в вершину с большим номером и при этом возможна последовательная нумерация вершин от 1 до n=|A|.
Будем использовать широко распространенный в программировании прием для сокращения решения комбинаторных задач - вначале тратятся добавочные усилия на предварительное упорядочение, затем в упорядоченном множестве более просто находят решение.
1. Упорядочим множество вершин так, чтобы любая дуга исходила
из вершины с меньшим номером и заходила в вершину с большим номе-
ром. Это можно сделать так: присвоим начальной вершине номер 1. Всем вершинам A ', связанным с начальной по исходящим дугам, сопоставим номера от 2 до |А’|. После этого проверим номера этих вершин на выполнение условия. Для любой пары вершин, где условие не выполняется, переставим номера вершин. Затем рассматриваются вершины, связанные по исходящим дугам с множеством А’ и т. д.
2. Присвоим всем вершинам вес l(i)=0.
3. Последовательно для вершин 1, 2, 3,... проведем пересчет весов
по формуле l(i) = m a x (l(i), l(j)+ C ji), где максимум берется по всем вершинам j, из которых есть дуги в вершину i. Это можно сделать, так как ко времени пересчета вершины i веса всех вершин j вычислены раньше, ибо i>j.
Сокращение вычислительных затрат по сравнению с алгоритмом Дейкстры связано с тем, что отпадает необходимость на каждом шаге определять очередную вершину с минимальным весом для продолжения расчетов.
4. Как и в алгоритме Дейкстры, выделим обратным ходом искомый путь.
12. Поток в сети. Поиск максимального потока.
Поток сети- функция, сопоставляющая дугам данной сети (ориентированного графа) нек-рые числа. Каждое число интерпретируется как интенсивность потока нек-рого груза по данной дуге. П. в с. являются удобной моделью при исследовании ряда проблем в транснорте, связи и др. областях, связанных с движением грузов, информации и т. д. Многие задачи о потоках являются задачами линейного программирования и могут решаться общими методами этой теории. Однако в большинстве случаев задачи о потоках допускают эффективное решение методами теории графов.
|
|
|


