 |
Проверка гипотезы о значении дисперсии генеральной совокупности
|
|
|
|
Проверка гипотезы о равенстве математических ожиданий двух генеральных совокупностей
Пусть из каждой из двух нормально распределенных генеральных совокупностей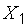 
(с параметрами 
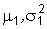) и 
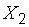(с параметрами 
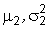) извлечены выборки объема 
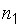и 
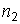соответственно. Требуется проверить нулевую гипотезу 
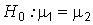о равенстве средних значений этих генеральных совокупностей. Альтернативная гипотеза формулируется в соответствии с условиями задачи или эксперимента:
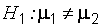(двустороння критическая область);
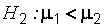(левостороння критическая область);
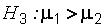(правостороння критическая область).
Случай, когда дисперсии генеральных совокупносте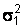й 
и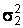 
известны. В этом случае для проверки нулевой гипотезы используют случайную величину
,
где 
– выборочные средние первой и второй выборок соответственно. Если нулевая гипотеза справедлива, то статистика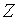 
имеет нормальное распределение с математическим ожиданием, равным нулю и дисперсией, равной единице (разд. 3). Критическое значение выбирается в соответствии с задаваемым уровнем значимости по таблице значений функции Лапласа (прил. 2) или стандартного нормального распределения.
Если объемы выборок достаточно велики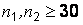 
, то случайную величину 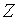можно использовать и при неизвестных дисперсиях генеральных совокупностей, положив в выражении для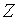 
, 
.
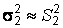Эту же статистику используют и при проверке гипотезы о равенстве вероятностей «успеха». Объемы выборок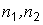 
должны быть достаточно велики, чтобы биномиальное распределение можно было бы приближенно считать нормальным.
Пример 4.7. Двое рабочих на одинаковых станках изготовляют одинаковые детали. Есть ли значимая разница между долями выпускаемого ими брака? Была собрана следующая информация: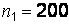 
, 
, 
, 
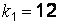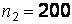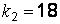(число деталей, изготовленных первым и вторым рабочими соответственно и число бракованных деталей у первого и второго рабочих). Положить 
.
|
|
|
Решение. Согласно условиям задачи требуется проверить нулевую гипотезу о равенстве значений вероятности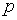 
«успеха» – появления бракованной детали ( 
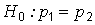) для первого и второго рабочего, причем, поскольку объем выборки достаточно велик, можно использовать статистику 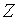. Поскольку 
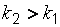, то альтернативную гипотезу следует принять в виде 
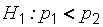(левосторонняя критическая область).
Итак, было обследовано 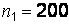деталей, изготовленных первым рабочим, из них 
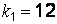– оказались бракованными, тогда
, 
.
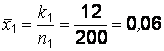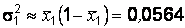Аналогично для второго рабочего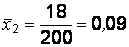 
, 
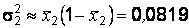. Тогда экспериментальное значение статистики:
.
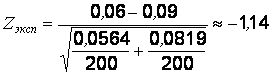Для критическое значение равно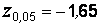 
, таким образом, 
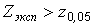. Следовательно, нулевая гипотеза отвергается: нельзя утверждать, что второй рабочий в среднем делает больше брака, чем первый.
Случай, когда дисперсии генеральных совокупносте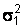й и 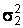неизвестны, но известно, что 
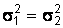. Для проверки нулевой гипотезы используется случайная величина
,
где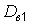 
и 
– выборочные дисперсии; 
– исправленные выборочные дисперсии.
Если нулевая гипотеза верна, то случайная величина 
имеет распределение Стьюдента с числом степеней свободы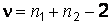 
(разд. 3). Критическое значение и критическая область выбираются в соответствии с альтернативной гипотезой и задаваемым уровнем значимости.
Проверка гипотезы о значении дисперсии генеральной совокупности
Пусть из нормально распределенной генеральной совокупности извлечена выборка объема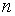 
. На основании полученных данных требуется проверить нулевую гипотезу о том, что дисперсия генеральной совокупности равна числу 
: 
. Альтернативная гипотеза чаще всего формулируется в виде: 
(левосторонняя критическая область).
|
|
|
Для проверки нулевой гипотезы используется случайная величина
,
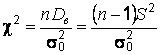где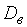 
– выборочная дисперсия, 
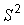– несмещенная оценка дисперсии генеральной совокупности.
Если нулевая гипотеза верна, то случайная величина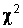 
имеет распределение 
с числом степеней свободы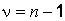 
(разд. 3). Критическое значение 
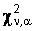определяется по таблице для заданного уровня значимости 
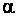из условия 
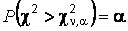(прил. 3).
Пример 4.8. Точность наладки станка-автомата, производящего некоторые детали, характеризуется дисперсией длины деталей. Если эта величина больше 400 мкм2, станок останавливают для наладки. Выборочная дисперсия длины 15 случайно отобранных деталей из продукции станка оказалась равной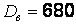 
мкм2. Нужно ли проводить наладку станка, если: а) уровень значимости 
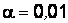; б) уровень значимости 
?
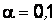Решение. По условию задачи требуется проверить нулевую гипотезу о значении дисперсии генеральной совокупности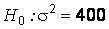 
мкм2 против альтернативной 
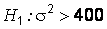(правосторонняя критическая область). Величина уровня значимости 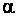определяет ширину критической области: чем больше 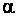, тем шире критическая область (рис. 4.3).
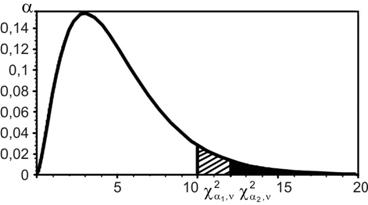
Рис. 4.3. Определение ширины критической области
По таблице распределения 
(прил. 3) учитывая 
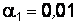и 
, 
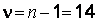, найдем критические значения 
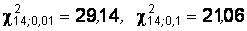. Вычислим экспериментальное значение статистики:
.
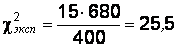Таким образом, если принять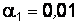 
, нулевая гипотеза не отвергается (станок не требует наладки). При 
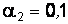нулевая гипотеза противоречит опытным данным, следовательно, станок нужно наладить.
|
|
|
