 |
При неизвестных и неравных дисперсиях
|
|
|
|
Смотри [Закс Л., с.248-252]. Проверяется гипотеза вида 
при условии, что 
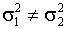. Такая задача получила название проблемы Беренса-Фишера
При неравных объемах выборок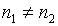 
статистика критерия имеет вид
,
а число степеней свободы
.
При равных объемах выборок 
–
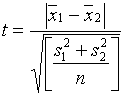
а
.
Сравнение средних значений двух малых выборок по Лорду
Смотри [Закс Л., с.254]. [Lord E., 1947]
Критерий предназначен для сравнения центров независимых рядов измерений равного объема ( 
). Статистика критерия имеет вид
,
где 
, 
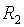– размахи выборок. Предполагается принадлежность наблюдений нормальному закону и равенство дисперсий. Утверждается, что критерий имеет такую же мощность (в табулированной области объемов выборок), как и t- критерий.
Проверяемая гипотеза отклоняется, когда значение статистики оказывается больше критического.
Сравнение средних значений нескольких выборок равного объема по Диксону
Смотри [Закс Л., с.255-256].
[Dixon., 1953]. Критерий используется для проверки значимости отклонения среднего одной выборки 
от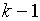 
средних значений других выборок. Предполагается, что является наименьшим или наибольшим в ряду средних значений 
, 
. Ряд средних значений упорядочивается либо по возрастанию 
, либо по убыванию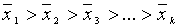 
. Статистика критерия имеет вид
.
Проверяемая гипотеза о незначимости отклонения от остальных отклоняется при больших значениях статистики. Рассматриваются варианты данной статистики. Считается, что критерий устойчив к нарушению предположений о нормальности наблюдаемого закона.
U-критерий Уилкоксона, Манна и Уитни
Смотри [Закс Л., с.270-281].
Ранговый критерий Манна и Уитни [Mann, Whitney, 1947] основан на критерии Уилкоксона для независимых выборок. Он является непараметрическим аналогом t- критерия для сравнения двух средних значений непрерывных распределений.
|
|
|
Асимптотическая эффективность U-критерия равна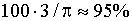 
по сравнению с t- критерием [Закс Л., с.270].
U-критерий Уилкоксона, Манна и Уитни проверяет гипотезу о принадлежности двух выборок одной и той же генеральной совокупности 
: 
. Эта гипотеза включает также равенство значений медиан 
и равенство средних значений 
.
Для вычисления статистики упорядочивают 
значений объединенной выборки, определяют сумму рангов , соответствующую элементам первой выборки, и сумму рангов второй 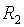. Вычисляем
,
.
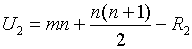Для контроля правильности можно использовать равенство 
. Статистика критерия имеет вид
.
Проверяемая гипотеза отклоняется, когда значение статистики оказывается меньше критического.
Считается, что U-критерий является самым строгим непараметрическим критерием.
Для достаточно больших выборок ( 
), когда объемы выборок не слишком малы ( 
), используется статистика
,
хорошо описываемая стандартным нормальным распределением [Mann H.B., Whitney D.R. On a test of whether one of two random variables is stochastically larger than the other // Ann. Math. Statist. 1947. V.18. – p. 50-60].
H-критерий Краскела-Уаллиса
Смотри [Закс Л., с.281-283], [Мардиа К., Земроч П., с. 24-27].
Данный критерий [Kruskal, Wallis, 1952] является развитием U-критерия для проверки гипотезы (о равенстве средних) по 
выборкам.
Объединенную выборку 
упорядочивают и вычисляют суммы рангов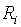 
для 
-й выборки, . Статистика для проверки нулевой гипотезы имеет вид
.
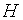представляет собой дисперсию ранговых сумм. При больших 
и (практически при 
, 
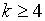) при справедливости проверяемой гипотезы 
статистика подчиняется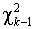 
-распределению. Проверяемая гипотеза отклоняется при больших значениях статистики.
Использованные литературы
1. http://ami.nstu.ru/~headrd/Tests_of_Mean_and_Cov.htm
|
|
|
2. http://edu.dvgups.ru/METDOC/ENF/PRMATEM/SPEC_GL_PRMATEM/METOD/UP/frame/frame_tema4_3.htm
3. www.google.ru
|
|
|
