Основная формула теории регулирования

Методы регулирования основаны на использовании обратной связи. Рассмотрим простую систему регулирования, имеющую один вход Х и выход Y (рис.3.4).

Имеется некоторая регулируемая система S, которая подвергается определенным воздействиям Х, дающим в итоге требуемый результат Y. Результат воздействует на регулятор R, который, в свою очередь, воздействует на регулируемую систему. Комплекс регулируемой системы и регулятора составляет систему регулирования. Преобразование состояния входа Х в состояние выхода Y формально можно отобразить как: 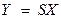. Этот способ отображения соответствует разомкнутому контуру управления. Как показано на рис. 3.4, состояние выхода регулируемой системы S передается на вход регулятора R, выходом которого является величина D X. Это состояние прибавляется к состоянию входа системы .

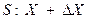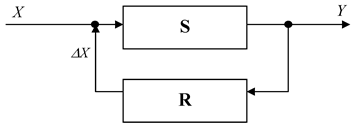
Рисунок 3.4 Система регулирования

Предположим, что регулируемая система работает как пропорциональный преобразователь: .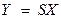

При 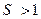пропорциональное преобразование называется усилением, а при 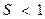– ослаблением. Показатель называется пропускной способностью регулируемой системы.

Предположим также, что регулятор тоже осуществляет пропорциональное преобразование, а его пропускная способность равна R. Тогда 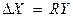.С учетом воздействия регулятора состояние выхода регулируемой системы определится как:

.

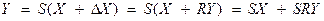Отсюда

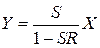. (3.15)

Выражение (3.15) является основной формулой теории регулирования. Приведенная формула дает возможность рассчитать необходимое значение входной величины, чтобы при заданных параметрах системы S и R получить на выходе искомый результат Y. Принимая во внимание то, что 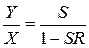, выражение 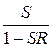называется пропускной способностью системы регулирования. Из основной формулы теории регулирования вытекает специфическая роль регулятора. При 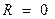пропускная способность регулируемой системы была бы равна . Наличие регулятора требует введения множителя 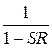, который характеризует его действие. Сомножитель 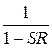выражает действие обратной связи в системе регулирования, и его называют оператором или мультипликатором обратной связи.

Регулирование как функция управления получила широкое применение в исследовании экономических систем управления.

Основные свойства и характеристики регулируемых систем изучаются технической кибернетикой в разделе теории автоматического управления.

Адаптивное управление

В тех случаях, когда воздействующие на систему факторы являются частично или полностью неопределенными, управление становится возможным только после накопления некоторой информации об этих факторах и характеристиках объекта. Управление в системе с полной априорной информацией об управляемом процессе, которое изменяется по мере накопления информации и применяется для улучшения качества работы системы, называется адаптивным управлением.

В дискретном времени 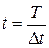, где Т — время, D t — интервал его квантования, процесс адаптивного управления может быть представлен следующим образом. Пусть управляемый процесс u является марковским процессом и описывается некоторой характеристикой информации Р.

Марковский процесс — случайный процесс, обобщенное понятие динамической системы, введенное А. Н. Колмогоровым, процесс, который обладает тем свойством, что его поведение после момента t зависит только от его значения в этот момент и не зависит от поведения процесса до момента t.

Пусть в момент t заданы состояние процесса u_t и состояние информации о процессе P_t, образующие точку (x_t, P_t)в некотором фазовом пространстве. Переход в новое состояние происходит под воздействием управления x_t и возмущения w _{t —} случайной величины с вероятностным распределением 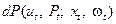, которое может являться какой-то частью характеристики информации. Переход в новое состояние может быть определен случайными преобразованиями S₁ и S₂ так, что:

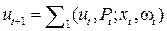; (3.16)

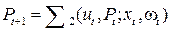. (3.17)

Управление х, изменяя состояние процесса u, влияет и на характеристику информации Р.

Если преобразования S₁ и S₂ заданы, то управление в момент перехода следует выбирать в виде:

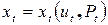. (3.18)

Управление (3.18) обладает свойством адаптации в том смысле, что оно зависит от всей доступной в момент t информации P_t о процессе. Но обычно преобразования S₁, S₂ не заданы, и определение этих преобразований, как и самой характеристики информации, является частью задачи об управлении с адаптацией. Для того чтобы информация о процессе со временем накапливалась, необходимо специально выбирать S₂ так, чтобы описание процесса P_t+1 было более полным, чем P_t. Изменения в направлении улучшения характеристик информации составляют сущность адаптации. Если с состоянием u_t+1 связать некоторый показатель качества управления 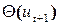, то за счет большей «информированности» управления вследствие адаптации этот показатель может улучшаться. При этом последовательность преобразований 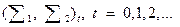дает процесс управления с адаптацией.

Таким образом, общее представление процесса адаптивного управления включает характеристику информации Р и механизм адаптации, определяемый преобразованием .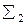

Двойственный характер адаптивного управления проявляется в том, что, с одной стороны, невозможно осуществлять эффективное управление, не зная характеристик объекта, с другой — можно изучать эти характеристики в процессе управления и тем самым улучшать его. Управляющие воздействия носят двойственный характер: они служат средством как активного познания управляемого объекта, так и непосредственного управления им в текущий момент времени.

В системах адаптивного управления обязательным является наличие обратной связи ввиду непрерывного процесса исследования характеристик объекта.

В системах управления, реализующих принцип адаптации, могут меняться параметры и структура системы (самоорганизация), программа, алгоритм функционирования и управляющие воздействия (самонастройка). Накопление и обобщение опыта обеспечивает возможности обучения и самообучения систем управления.

Адаптивное управление в полной мере присуще системам управления в живой природе. Она дает нам образцы совершенной организации, настройки и функционирования систем управления сложнейшими динамическими процессами, которые современная теория и практика управления стремиться воспроизвести в искусственных системах. Адаптация в экономических системах проявляется в способности системы сохранять в процессе развития существенные параметры не изменяющимися в определенных границах их варьирования, несмотря на разнообразие воздействий внешней среды.

 

 

3.4 Принципы и законы управления

Подведем некоторые итоги обсуждения концепции управления, содержание которого определяется, прежде всего, целью, ради достижения которой оно осуществляется. Сущность управления близка его содержанию и характеризуется целенаправленностью, присущей любым видам систем и процессов управления. Управление реализуется в системах различной природы, в специфических условиях, что создает сложности в процессе их исследования. Методологической базой исследования систем и процессов управления является комплекс принципов, учет которых обеспечивает многообразие, актуальность и эффективность их применения. В главе 3 были рассмотрены следующие принципы, собранные в таблице 3.1.

Таблица 3.1 – Принципы и законы управления

Принципы и законы исследования систем управления	Принципы и законы исследования процессов управления
1. целостность 2. системный подход 3. организованность 4. динамичность 5. управляемость 6. оптимальность 7. многокритериальность 8. многофункциональность	1. необходимое разнообразие 2. внешнее дополнение 3. иерархичность управления 4. адаптивность управления 5. обязательность обратной связи 6. управление воздействием на главный фактор 7. принятие решений на основе отбора и преобразования информации

Глава 4
ИНФОРМАЦИЯ

Рассмотрим какую-нибудь большую систему. По определению эта система является сложной. Степень сложности измеряется разнообразием системы. Терминразнообразие достаточно наглядно определяет числом различимых состояний системы. Рассмо­трим теперь нашу систему как кибернетическую машину для переработки информации. По существу это основная функция кибернетической машины. Даже в том случае, когда в нее входит какой-либо физический механизм, совершенно очевидна приоритетная роль, которую играет способность хранить, передавать и преобразовывать информацию в работе этого механизма. Такая кибернетическая машина обладает большим разнообразием, а, следовательно, характеризуется большой неопределенностью. Сле­дует отметить, что системы очень сложного типа описываются при помощи аппарата теории вероятностей, так как с увеличением разнообразия увеличивается число возможных состояний системы и усложняется ее математическое опи­сание.

Кибернетическая машина в первоначальном состоянии полна неопределенности, ее поведение хаотично. Однако, как только она начинает работать, в ней появляется упорядоченность, которая начинает уничтожать царящую неопределенность. Эта особенность — появление информации — и позволяет нам управлять кибернетическими системами. Информация уничтожает разнообразие, а уменьшение разнообразия является одним из основных методов регулирования, и не потому, что при этом упрощается управляемая система, а потому, что поведение системы становится более предсказуемым. Наличие «шума» в системе ведет к увеличению разнообразия (а, следова­тельно, и неопределенности), не увеличивая содержащейся в ней информации.

Стаффорд Бир

 

Информация – (лат. informatio — разъяснение, изложение, осведомленность) неотъемлемый элемент любого процесса управления в экономических, технических системах, обществе, живом организме.

Информация – основное понятие кибернетики, точно так же экономическая информация – основное понятие экономической кибернетики.

Определений этого термина много, они сложны и противоречивы. Причина этого в том, что информацией как явлением кроме кибернетики занимается много разных наук, таких как математическая статистика, генетика, теория средств массовой информации (печать, радио, телевидение), информатика, занимающаяся проблемами научно-технической информации и т.д. Наконец, в последнее время большой интерес к проблемам информации проявляют философы: они склонны рассматривать информацию как одно из основных универсальных свойств материи, связанное с понятием отражения.

Тем не менее, все определения информации предполагают существование двух объектов: источника информации и потребителя (получателя) информации. В общем понимании информация отождествляется с каким-либо известием, которое может иметь форму устного сообщения, письма, доклада, результатов исследования, наблюдения и пр. Н. Винер писал, что в кибернетике под информацией понимается не только обмен между человеком и машиной, но и обозначение содержания, полученного из внешнего мира в процессе нашего приспособления к нему и приспособления к нему наших чувств. Таким образом, передача информации происходит с помощью сигналов, которые, вообще говоря, могут не иметь никакой физической связи с ее смыслом: эта связь определяется соглашением и те кто вовлечен в это соглашение – понимают этот сигнал, а те кто нет – могут просто его воспринимать и никак на него не реагировать. Например, большой цветок в окне для Плейшнера означал одно: явка провалена, в то время как все остальные просто им любовались. То есть, можно сказать, что принятый и распознанный сигнал приводит к уменьшению неопределенности. Однако, если неопределенности нет, то сигнал ничего нового не сообщает. Из этого следует, что, чем более неожиданно сообщение, тем больше информации оно содержит, и наоборот, чем больше вероятность исхода до совершения события, тем меньше информации содержит сигнал о его наступлении.

Процесс передачи информации может рассматриваться как прохождение трех фильтров:

1) физического, или статистического (количественное ограничение по пропускной способности канала, независимо от содержания данных, т.е. с точки зрения синтаксиса, или физической возможности восприятия сигналов);

2) семантического (отбор тех данных, которые могут быть поняты получателем, т.е. соответствуют тезаурусу его знаний);

3) прагматического (отбор среди понятых сведений тех, которые полезны для решения данной задачи).

По содержанию информация подразделяется на общественно-политическую. Социально-экономическую (в том числе экономическую), научно-техническую и т.д.

Вообще же классификаций информации много, они строятся по различным основаниям:

статическая и динамическая;

первичная, производная и выходная;

управляющая и осведомляющая;

избыточная, полезная и ложная;

полная и выборочная и т.д.

Таким образом, под информацией понимается сообщение, устраняющее неопределенность в той области, к которой оно относится. Академик В. М. Глушков дал следующее определение:

информация – это мера неоднородности распределения материи и энергии в пространстве и во времени, показатель изменений, которыми сопровождаются все протекающие в мире процессы.

Примерно такие рассуждения привели в 40-х годах XX в. К возникновению статистической, или «классической» теории информации, которая определяет понятие информации через меру уменьшения неопределенности знания о свершении какого-либо события (такая мера была названа энтропией). У истоков этой науки стояли Н.Винер, К.Шеннон и советские ученые А.Н.Колмогоров, В.А. Котельников и др. Им удалось вывести математические закономерности измерения количества информации, а отсюда и такие понятия, как пропускная способность канала информации, емкость запоминающих информационных устройств и т.п.

Важнейшим инструментом исследования информации является теория информации, посвященная проблемам сбора, передачи, хранения, переработки и определения количественной меры информации.

Создателями теории информации явились Л. Хартли, К. Шеннон, А. А. Харкевич, С. Гольдман и др. Основы статистической теории информации сформулированы, главным образом, К. Шенноном. Но теория Шеннона оказалась применимой к довольно широкому кругу вопросов, хотя она и не претендует на адекватное отображение всего содержания информации, употребляемого в науке и в обыденной жизни в различном смысле.

Что касается определения ценности информации для получателя, то здесь еще много нерешенного, неясного. Если исходить из потребностей экономического управления и, следовательно, экономической кибернетики, то информацию можно определить как все те сведения, знания, сообщения, которые помогают решить ту или иную задачу управления (т.е. уменьшить неопределенность ее исходов). Тогда открываются и некоторые возможности для оценки информации: она тем полезнее, ценнее, чем скорее или с меньшими затратами приводит к решению задачи.

 

 

4.1 Количественное измерение информации

Информацию можно измерить количественно, подсчитать. Для этого абстрагируются от смысла сообщения. Шеннон дал формальное определение количества информации на основе вероятностного подхода и указал критерий, позволяющий сравнивать количество информации, доставляемое разными сигналами.

Смысл заключается в том, что между сигналом и событием су­ществует однозначная связь. Совокупность сигналов является изоморфным отображением некоторых сторон реального события. Связь сигнала с событием воспринимается как смысловое содержание сигнала или сообщения, сущность которого состоит в том, что благодаря ему получатель по­буждается к выбору определенного поведения. Всякое сообщение может рассматриваться как сведения об определенном событии x_i в момент t_i. Это событие содержит данные о том, в каком из множества возможных состояний находилась система S в момент времени t_i. Процесс связи предполагает наличие множества возможностей. У. Р. Эшби приводит следующий пример.

Заключенного должна навестить жена. Сторож знает, что она хочет сообщить мужу, пойман ли его сообщник. Ей не разрешено делать никаких сообщений. Но сторож подозревает, что они договорились о каком-то условном знаке. Вот она просит послать мужу чашку кофе. Как сторож может добиться, чтобы сообщение не было передано? Он будет рассуждать так: может быть, она условилась передать ему сладкий или несладкий кофе, тогда я могу помешать, добавив в кофе сахару и сказав об этом за­ключенному. Может быть, она условилась послать или не послать ему ложку, тогда я помешаю, изъяв ложку и сказав ему, что передача ложек воспрещена. Она может послать ему не кофе, а чай, но все знают, что в это время выдается только кофе. Как видно, сторож интуитивно стремится пресечь всякую возможность связи. Для этого он сводит все возможности к одной — только с сахаром, только без ложки, только кофе. Если все возможности сведены к одной, связь прерывается, и посылаемый напиток лишен возможности передать информацию. Из этого примера видно, что передача и хранение информации существенно связаны с наличием некоторого множества возможностей.

Кроме того, информация, передаваемая отдельным сообщением, зависит от того множества, из которого оно выбрано. Например, два солдата находятся в плену — один в стране А, другой в стране В. Им разрешили послать женам телеграммы с содержанием «Я здоров». Однако известно, что в стране А пленным разрешается выбирать следующие сообщения: я здоров, я слегка болен, я серьезно болен. В стране В разрешается сообщать только: я здоров, означающее — я жив. Обе женщины получили одинаковую фразу, но они будут понимать, что полученная ими информация не является тождественной. Из этого примера видно, что передаваемая информация не является внутренним свойством индивидуального сообщения. Она зависит от того множества, из которого выбрана.

Если система может находиться в одном из N различных состояний, множество которых x₁, x₂, …, x_N известно получателю сообщения, то для передачи сведений о состоянии системы достаточно указать номер 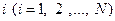состояния, в котором она находится.

Длина последовательности, необходимой для передачи некоторого сообщения, пропорциональна логарифму числа возможных сообщений. Если статистические связи между символами отсутствуют, то максимальное количество информации (H_max) _, которое содержится в сообщении, пропорционально его длине:

.

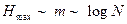Эта мера максимального количества информации, которое может содержаться в сообщении, предложена в 1928 г. американским ученым Л. Хартли. Мера максимального количества информации обладает двумя важнейшими свойствами: она монотонно возрастает с возрастанием N и является аддитивной. Свойство аддитивности означает следующее: сообщение а выбирается из N₁ возможных сообщений, независимое от а сообщение b выбирается из N₂ возможных сообщений. Информация, которая содержится в сложном сообщении, состоящем из сообщения а и сообщения b, зависит от числа возможных сложных сообщений, их 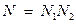. Отсюда:

.

Очевидно, что в сложном сообщении содержится сумма информации, которую несут отдельные сообщения, что согласуется с интуитивными представлениями.

Величина 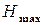указывает верхнюю границу количества информации, которое может содержаться в сообщении. Однако действительное количество информации зависит не только от числа возможных сообщений, но и от их вероятностей. Заслуга К. Шеннона состоит в том, что он указал на существование неопределенности относительно того, какое именно конкретное сообщение из множества сообщений отправителя будет выбрано для передачи. Это связывает информацию с теорией вероятностей. Оценка количества информации основывается на законах теории вероятностей. Сообщение имеет ценность, оно несет информацию только тогда, когда мы узнаем из него об исходе события, имеющего случайный характер, когда оно в какой-то мере неожиданно.

 

4.2 Неопределенность

Понятия возможности, случайности, вероятности находятся в определенном отношении с понятием неопределенности. Неопределенность существует объективно. Она всегда имеет место тогда, когда производится выбор из некоторой совокупности элементов. Степень неопределенности выбора характеризуется отношением числа выбранных элементов к общему числу элементов совокупности (множества). Таким образом, степень неопределенности обратно пропорциональна количеству возможных способов выбора элементов из множества. Если множество состоит из одного элемента, то степень неопределенности равна нулю. Одной из оценок степени неопределенности Н через вероятность р является логарифм величины :

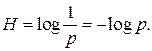(4.1)

Изучением степени неопределенности и связи ее с вероятностью занимается статистическая теория информации. Формула 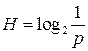является логарифмической мерой количества информации. В теории информации рассматриваются любые события, в результате которых уменьшается степень неопределенности.

Для оценки количества информации, связанной с появлением одного сообщения, пользуются формулой:

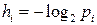, (4.2)

где 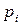– вероятность появления события .

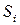Такую оценку индивидуального количества информации называют индивидуальной энтропией. Индивидуальная энтропия события тем больше, чем меньше вероятность его появления. Однако статистическую теорию информации не интересует индивидуальное количество информации. Существенной для характеристики любого опыта являются не информации 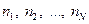, связанные с отдельными исходами опыта, а средняя информация, которая определяется следующим образом.

Пусть для некоторого события х известно, что количество различных исходов равно N, а вероятности их равны соответственно 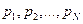, причем .

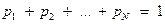В результате достаточно большого числа испытаний (их число равно М)получено, что первый исход наступил m₁ раз, второй — m₂ раз,.., N -й — m_N раз . Известно, что в результате единичного наступления i -го исхода опыта получаем индивидуальное количество информации:

.

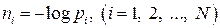Поскольку первый исход наступил m₁ раз, то полученное при этом суммарное количество информации равно n₁ m₁, где n₁ – индивидуальное количество информации, полученное в результате одного наступления первого исхода опыта. Аналогично получаем суммарное количество информации, полученное при наступлении второго исхода опыта и т. д. Общее количество информации, полученное в результате М испытаний, равно

,

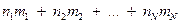а среднее количество информации, полученное в одном испытании, равно

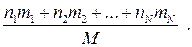
При .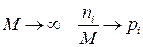

Отсюда получаем среднее количество информации, харак­теризующее событие х:

.

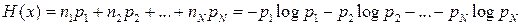Предположим, что опыт состоит в извлечении одного шара из ящика, в котором находится один черный и два белых шара. Исходя из классического подхода, вероятность выбора черного шара равна 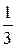, а вероятность выбора белого шара равна 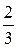. Среднее значение неопределенности полу­чается, если вероятность отдельного исхода умножается на его неопределенность, и эти произведения складываются:

.

В общем виде формула степени неопределенности (количества информации в битах) имеет следующий вид:

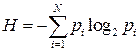. (4.3)

Эта формула предложена в 1948 г. К. Шенноном. Ее называют еще формулой абсолютной негэнтропии. Она аналогична формуле энтропии, только имеет отрицательный знак.

 

Для оценки среднего количества информации в сообщениях при неравновероятных исходах используется следующая формула:

Запишем формулу Шеннона в виде:

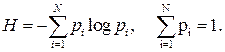
Пусть все исходы равновероятны, тогда:

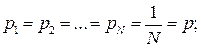
подставив эти значения в формулу, получим:

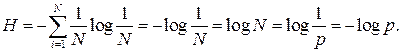
Из формулы степени неопределенности видно, что среднее количество информации в битах в дискретном сообщении о простом событии определяется как отрицательная сумма вероятностей всех возможных событий, умноженных на их логарифмы по основанию 2. Количество информации выше среднего приходится на события, вероятность которых ниже. Более высокую информационную емкость имеют редкие события. Формулой подтверждается также более низкая неопределенность систем с более высокой вероятностью событий. Поскольку вероятность одних событий повышается за счет снижения вероятности других (так как сумма всех вероятностей равна 1), энтропия становится тем ниже, чем менее вероятны события, а максимума она достигает при равновероятности всех событий.

Покажем, что H_max, получаемое при равновероятных исходах события, является верхней границей значений Н. Для этого найдем максимальное значение функции

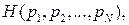
используя метод множителей Лагранжа.

Приравняем к нулю частные производные функции по :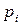

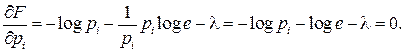
Отсюда 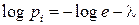и легко видеть, что все , следовательно, . Если же событие является достоверным (при этом 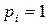, а остальные ), то

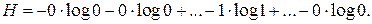
Легко показать, что выражение 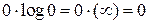. Раскроем неопределенность, используя правило Лопиталя:

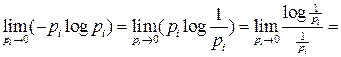
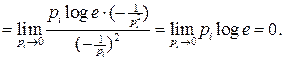
Тогда получим для достоверного события.

Следовательно, среднее количество информации находится в пределах

.

Для зависимых событи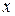й и 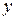средняя неопределенность события 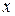при любых возможных исходах события у равна:

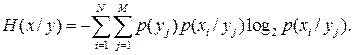(4.8)

Это условная негэнтропия случайной величины 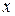при задании случайной величины 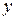. Она всегда не больше безусловной

,

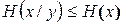причем равенство имеет место только в том случае, когда знание величины 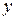не меняет вероятностей значений величины 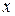, т. е.

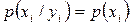
Это означает, что неопределенность события 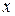не изменяется при получении дополнительной информации о событии .

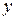Для двух случайных событий х и у энтропия совместного события равна:

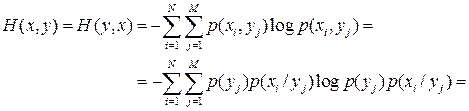
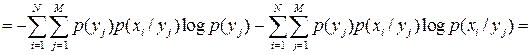
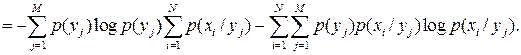
В полученном выражении

,

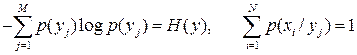а второе слагаемое есть не что иное, как .

Следовательно,

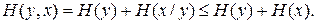(4.9)

Равенство достигается тогда, когда события 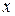и 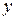независимы.

В качестве меры количества информации в случайной величине 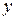о случайной величине 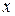принимается величина, на которую уменьшается в среднем неопределенность величины 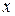, если нам становится известным значение величины :

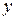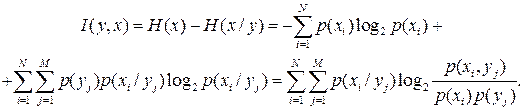
Эта формула выражает количество информации в случайной величине 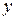о случайной величине 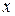, как разность между безусловной и условной негэнтропией.

По формуле условной негэнтропии строится вся современная статистическая теория информации. Переход от абсолютной негэнтропии к условной приобретает фундаментальное решающее значение. Формула условной негэнтропии выражает количество информации относительно заданной системы отсчета, системы координат. Иначе говоря, она характеризует количество информации, содержащееся в одном объекте относительно другого объекта.

Классическая теория информации дает полезный аппарат, но он не универсален и множество ситуаций не укладываются в информационную модель Шеннона. Далеко не всегда можно заранее установить перечень возможных состояний системы и вычислить их вероятности. Кроме того, основным недостатком этой теории является то, что, занимаясь только формальной стороной сообщений, она оставляет в стороне их ценность и важность. Например, система радиолокационных станций ведет наблюдение за воздушным пространством с целью обнаружения самолета противника. Система S, за которой ведется наблюдение, может быть в одном из двух состояний: x₁ – противник есть, х₂ – противника нет. Выяснение фактического состояния системы принесло бы в рамках классической теории информации 1 бит, однако первое сообщение гораздо важнее, что оценить невозможно с помощью вероятностного подхода.

Статистическая теория информации оперирует лишь вероятностями исходов рассматриваемых опытов и полностью игнорирует содержание этих исходов. Поэтому эта теория не может быть признана пригодной во всех случаях. Понятие информации в ней трактуется весьма односторонне.

Следовательно, уничтожение неопределенности, т. е. получение информации, может происходить не только в результате вероятностного процесса, но и в других формах. Понятие неопределенности оказывается шире понятия вероятности. Неопределенность — понятие, отражающее отсутствие однозначности выбора элементов множества. Если этот выбор имеет случайный характер, то мы имеем дело со статистической теорией информации. Если же этот выбор не случаен, то необходим невероятностный подход к определению информации. Существуют следующие невероятностные подходы к определению информации: динамический, топологический, алгоритмический. Мы не будем рассматривать эти невероятностные подходы к определению количества информации, отметим только, что каждый из этих методов обнаруживает нечто общее со статистическим подходом. Оно состоит в том, что эти методы изучают переход от неопределенности к определенности. Но все же эти методы отличаются от статис­тического подхода. Один из невероятностных подходов к определению количества информации принадлежит советскому ученому А. Н. Колмогорову. По аналогии с вероятностным определением количества информации как функции связи двух систем, он вводит определение алгоритмического количества информации.

Количество информации, содержащееся в сообщении, можно связывать не только с мерой неопределенности системы, но и с ее структурной сложностью и точностью измерений. Такой подход предлагается к оценке научной информации, возникающей в результате анализа процесса наблюдений и эксперимента.

Количество различных признаков, характеризующих данный предмет, т. е. его размерность или число степеней свободы, является мерой структурной информации. Ясно, что цветное изображение содержит в себе больше информации по сравнению с черно-белым изображением того же объекта. Единица структурной информации — логон — означает, что к имеющемуся представлению можно добавить одну новую различимую группу или категорию.

Количество метрической информации связано с разрешающей способностью измерений. Например, эксперимент, результат которого обладает погрешностью, равной 1 %, дает больше информации, чем эксперимент, характеризующийся погрешностью в 10 %.

Единицей измерения метрической информации является метрон. В случае числового параметра эта единица служит мерой точности, с которой этот параметр определен.

Статистический и нестатистический подходы в теории информации касаются только количества информации, но информация имеет еще и качественный аспект. Объединение элементов в множество всегда предполагает наличие у них некоторого свойства, признака, благодаря чему они образуют данное множество, а не иное. Следовательно, каждый элемент множества обладает определенным качественным отличием от элемента другого множества. Кроме того, внутри множества различие элементов друг от друга носит тоже качественный характер. Поиск качественного аспекта информации как раз и состоит в учете природы элементов, объединяемых в множества, в учете качественного многообразия материи.

До сих пор информация рассматривалась как снятая, устраняемая неопре

⇐ Предыдущая123456Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: