|
Метод управления и интерпретация контрольных карт для количественных данных
|
|
|
|
Статистические методы
КОНТРОЛЬНЫЕ КАРТЫ ШУХАРТА
Statistical methods.
Shewhart control charts
Дата введения 2000-01-01
Область применения
Настоящий стандарт устанавливает основные положения по применению и интерпретации контрольных карт Шухарта (далее - карт Шухарта) и соответствующих методов статистического управления процессами.
Дополнительный материал, связанный с подходом Шухарта, а именно, использование предупреждающих границ, анализ структур тренда и возможности процессов, лишь упомянут. Кроме того, существуют другие типы контрольных карт [2].
Обозначения и сокращения
n - объем подгруппы, число выборочных наблюдений в подгруппе;
k - число подгрупп;
X - измеряемая характеристика качества (индивидуальные значения записываются как (Х 1, Х 2, Х 3...)). Иногда вместо X используют Y;
 - среднее значение для подгруппы,
- среднее значение для подгруппы,  ;
;
 - среднее средних значений подгрупп;
- среднее средних значений подгрупп;
m - истинное среднее процесса;
Me - медиана подгруппы. Для выборки объема n, значения Х 1, Х 2, Хn которой упорядочены по возрастанию или по убыванию, медиана есть центральное значение, если n нечетно, и среднее двух центральных значений, если n четно;
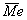 - среднее значение медиан подгрупп;
- среднее значение медиан подгрупп;
R - размах подгруппы (разность наибольшего и наименьшего значений в подгруппе);
Примечание - В случае контрольной карты индивидуальных наблюдений R представляет собой скользящий размах, то есть абсолютную разность двух последовательных значений | Х 1 - Х 2|, | Х 2 - Х 3|и т.д.
 - среднее значение R для всех подгрупп;
- среднее значение R для всех подгрупп; 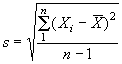
s - выборочное стандартное (среднее квадратическое) отклонение;
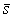 - среднее выборочных стандартных (средних квадратических) отклонений подгрупп;
- среднее выборочных стандартных (средних квадратических) отклонений подгрупп;
s - истинное внутригрупповое стандартное отклонение;
|
|
|
 - оцененное внутригрупповое стандартное отклонение процесса;
- оцененное внутригрупповое стандартное отклонение процесса;
nр - число несоответствующих единиц в подгруппе;
р - доля несоответствующих единиц в подгруппе

 - среднее значение доли несоответствующих единиц
- среднее значение доли несоответствующих единиц

с - число несоответствий в подгруппе;
 - среднее значений с для всех подгрупп;
- среднее значений с для всех подгрупп;
и - число несоответствий на единицу в подгруппе;
 - среднее значение и
- среднее значение и

CL - центральная линия;
UCL - верхняя контрольная граница;
LCL - нижняя контрольная граница.
3 Основы контрольных карт Шухарта
Карта Шухарта требует данных, получаемых выборочно из процесса через примерно равные интервалы. Интервалы могут быть заданы либо по времени (например ежечасно), либо по количеству продукции (каждая партия). Обычно каждая подгруппа состоит из однотипных единиц продукции или услуг с одними и теми же контролируемыми показателями, и все подгруппы имеют равные объемы. Для каждой подгруппы определяют одну или несколько характеристик, таких как среднее арифметическое подгруппы  и размах подгруппы R или выборочное стандартное отклонение и размах подгруппы R или выборочное стандартное отклонение  . Карта Шухарта - это график значений определенных характеристик подгрупп в зависимости от их номеров. Она имеет центральную линию (CL), соответствующую эталонному значению характеристики. При оценке того, находится ли процесс в статистически управляемом состоянии, эталонным обычно служит среднее арифметическое рассматриваемых данных. При управлении процессом эталонным служит долговременное значение характеристики, установленное в технических условиях, или ее номинальное значение, основанное на предыдущей информации о процессе, или намеченное целевое значение характеристики продукции или услуги. Карта Шухарта имеет две статистические определяемые контрольные границы относительно центральной линии, которые называются верхней контрольной границей (UCL) и нижней контрольной границей (LCL) (рисунок 1). . Карта Шухарта - это график значений определенных характеристик подгрупп в зависимости от их номеров. Она имеет центральную линию (CL), соответствующую эталонному значению характеристики. При оценке того, находится ли процесс в статистически управляемом состоянии, эталонным обычно служит среднее арифметическое рассматриваемых данных. При управлении процессом эталонным служит долговременное значение характеристики, установленное в технических условиях, или ее номинальное значение, основанное на предыдущей информации о процессе, или намеченное целевое значение характеристики продукции или услуги. Карта Шухарта имеет две статистические определяемые контрольные границы относительно центральной линии, которые называются верхней контрольной границей (UCL) и нижней контрольной границей (LCL) (рисунок 1).
 Рисунок 1 - Вид контрольной карты
Контрольные границы на карте Шухарта находятся на расстоянии 3s от центральной линии, где s - генеральное стандартное отклонение используемой статистики. Изменчивость внутри подгрупп является мерой случайных вариаций. Для получения оценки s вычисляют выборочное стандартное отклонение или умножают выборочный размах на соответствующий коэффициент. Эта мера не включает межгрупповых вариаций, а оценивает только изменчивость внутри подгрупп.
Границы ± 3s указывают, что около 99,7 % значений характеристики подгрупп попадут в эти пределы при условии, что процесс находится в статистически управляемом состоянии. Другими словами, есть риск, равный 0,3 % (или в среднем три на тысячу случаев), что нанесенная точка окажется вне контрольных границ, когда процесс стабилен. Употребляется слово «приблизительно», поскольку отклонения от исходных предположений, таких как вид распределения данных, будут влиять на значения вероятности.
Некоторые консультанты предпочитают вместо множителя, равного 3, значение 3,09, чтобы обеспечить номинальное значение вероятности 0,2 % (в среднем два вводящих в заблуждение наблюдения на тысячу), но Шухарт выбрал число 3, чтобы не давать поводов к рассмотрению точных вероятностей. Аналогично некоторые консультанты применяют фактические значения вероятностей для карт, основанных на ненормальных распределениях, таких как карты размахов и долей несоответствий, и в этом случае в карте Шухарта также используют границы на расстоянии ± 3s вместо вероятностных пределов, упрощая эмпирическую интерпретацию.
Вероятность того, что нарушение границ в самом деле случайное событие, а не реальный сигнал, считается столь малой, что при появлении точки вне границ следует предпринять определенные действия. Так как действие предпринимается именно в этой точке, то 3s контрольные границы иногда называются «границами действий».
Часто на контрольной карте границы проводят еще и на расстоянии 2s. Тогда любое выборочное значение, попадающее за границы 2s, может служить предостережением о грозящей ситуации выхода процесса из состояния статистической управляемости. Поэтому границы ± 2s иногда называют «предупреждающими».
При применении контрольных карт возможны два вида ошибок: первого и второго рода.
Ошибка первого рода, возникает, когда процесс находится в статистически управляемом состоянии, а точка выскакивает за контрольные границы случайно. В результате неправильно решают, что процесс вышел из состояния статистической управляемости, и делают попытку найти и устранить причину несуществующей проблемы.
Ошибка второго рода возникает, когда рассматриваемый процесс не управляем, а точки случайно оказываются внутри контрольных границ. В этом случае неверно заключают, что процесс статистически управляем и упускают возможность предупредить рост выхода несоответствующей продукции. Риск ошибки второго рода - функция трех факторов: ширины контрольных границ, степени неуправляемости и объема выборки. Их природа такова, что можно сделать лишь общее утверждение о величине ошибки.
Система карт Шухарта учитывает только ошибки первого рода, равные 0,3 % в пределах границ 3s. Поскольку в общем случае непрактично делать полную оценку потерь от ошибки второго рода в конкретной ситуации, а удобно произвольно брать малый объем подгруппы (4 или 5 единиц), целесообразно использовать границы на расстоянии ± 3s и сосредоточивать внимание в основном на управлении и улучшении качества самого процесса.
Если процесс статистически управляем, контрольные карты реализуют метод непрерывной статистической проверки нулевой гипотезы о том, что процесс не изменился и остается стабильным. Но поскольку значение конкретного отклонения характеристики процесса от цели, которое могло бы привлечь внимание, обычно нельзя определить заранее, как и риск ошибки второго рода, и объем выборки не рассчитывается для удовлетворения соответствующего уровня риска, то карту Шухарта не стоит рассматривать с точки зрения проверки гипотез [2, 3]. Шухарт подчеркивал именно эмпирическую полезность контрольных карт для установления отклонений от состояния статистической управляемости, а не их вероятностную интерпретацию. Некоторые пользователи применяют кривые оперативных характеристик как средства для интерпретации проверок гипотез.
Когда наносимое значение выходит за любую из контрольных границ или серия значений проявляет необычные структуры, (раздел 7), состояние статистической управляемости подвергается сомнению. В этом случае надо исследовать и обнаружить неслучайные (особые) причины, а процесс можно остановить или скорректировать. Как только особые причины найдены и исключены, процесс снова готов к продолжению работы. При возникновении ошибки первого рода можно не найти никакой особой причины. Тогда считают, что выход точки за границы представляет собой достаточно редкое случайное явление при нахождении процесса в статистически управляемом состоянии.
Если контрольную карту процесса строят впервые, то часто оказывается, что процесс статистически неуправляем. Контрольные границы, рассчитанные на основе данных такого процесса, будут иногда приводить к ошибочным заключениям, поскольку они могут оказаться слишком широкими. Следовательно, прежде чем устанавливать постоянные параметры контрольных карт, надо привести процесс в статистически управляемое состояние.
4 Типы контрольных карт
Контрольные карты Шухарта бывают двух основных типов: для количественных и альтернативных данных. Для каждой контрольной карты встречаются две ситуации:
а) стандартные значения не заданы;
б) стандартные значения заданы.
Стандартные значения - значения, установленные в соответствии с некоторыми конкретными требованиями или целями.
4.1 Контрольные карты, для которых не заданы стандартные значения
Цель таких карт - обнаружение отклонений значений характеристик (например,
Рисунок 1 - Вид контрольной карты
Контрольные границы на карте Шухарта находятся на расстоянии 3s от центральной линии, где s - генеральное стандартное отклонение используемой статистики. Изменчивость внутри подгрупп является мерой случайных вариаций. Для получения оценки s вычисляют выборочное стандартное отклонение или умножают выборочный размах на соответствующий коэффициент. Эта мера не включает межгрупповых вариаций, а оценивает только изменчивость внутри подгрупп.
Границы ± 3s указывают, что около 99,7 % значений характеристики подгрупп попадут в эти пределы при условии, что процесс находится в статистически управляемом состоянии. Другими словами, есть риск, равный 0,3 % (или в среднем три на тысячу случаев), что нанесенная точка окажется вне контрольных границ, когда процесс стабилен. Употребляется слово «приблизительно», поскольку отклонения от исходных предположений, таких как вид распределения данных, будут влиять на значения вероятности.
Некоторые консультанты предпочитают вместо множителя, равного 3, значение 3,09, чтобы обеспечить номинальное значение вероятности 0,2 % (в среднем два вводящих в заблуждение наблюдения на тысячу), но Шухарт выбрал число 3, чтобы не давать поводов к рассмотрению точных вероятностей. Аналогично некоторые консультанты применяют фактические значения вероятностей для карт, основанных на ненормальных распределениях, таких как карты размахов и долей несоответствий, и в этом случае в карте Шухарта также используют границы на расстоянии ± 3s вместо вероятностных пределов, упрощая эмпирическую интерпретацию.
Вероятность того, что нарушение границ в самом деле случайное событие, а не реальный сигнал, считается столь малой, что при появлении точки вне границ следует предпринять определенные действия. Так как действие предпринимается именно в этой точке, то 3s контрольные границы иногда называются «границами действий».
Часто на контрольной карте границы проводят еще и на расстоянии 2s. Тогда любое выборочное значение, попадающее за границы 2s, может служить предостережением о грозящей ситуации выхода процесса из состояния статистической управляемости. Поэтому границы ± 2s иногда называют «предупреждающими».
При применении контрольных карт возможны два вида ошибок: первого и второго рода.
Ошибка первого рода, возникает, когда процесс находится в статистически управляемом состоянии, а точка выскакивает за контрольные границы случайно. В результате неправильно решают, что процесс вышел из состояния статистической управляемости, и делают попытку найти и устранить причину несуществующей проблемы.
Ошибка второго рода возникает, когда рассматриваемый процесс не управляем, а точки случайно оказываются внутри контрольных границ. В этом случае неверно заключают, что процесс статистически управляем и упускают возможность предупредить рост выхода несоответствующей продукции. Риск ошибки второго рода - функция трех факторов: ширины контрольных границ, степени неуправляемости и объема выборки. Их природа такова, что можно сделать лишь общее утверждение о величине ошибки.
Система карт Шухарта учитывает только ошибки первого рода, равные 0,3 % в пределах границ 3s. Поскольку в общем случае непрактично делать полную оценку потерь от ошибки второго рода в конкретной ситуации, а удобно произвольно брать малый объем подгруппы (4 или 5 единиц), целесообразно использовать границы на расстоянии ± 3s и сосредоточивать внимание в основном на управлении и улучшении качества самого процесса.
Если процесс статистически управляем, контрольные карты реализуют метод непрерывной статистической проверки нулевой гипотезы о том, что процесс не изменился и остается стабильным. Но поскольку значение конкретного отклонения характеристики процесса от цели, которое могло бы привлечь внимание, обычно нельзя определить заранее, как и риск ошибки второго рода, и объем выборки не рассчитывается для удовлетворения соответствующего уровня риска, то карту Шухарта не стоит рассматривать с точки зрения проверки гипотез [2, 3]. Шухарт подчеркивал именно эмпирическую полезность контрольных карт для установления отклонений от состояния статистической управляемости, а не их вероятностную интерпретацию. Некоторые пользователи применяют кривые оперативных характеристик как средства для интерпретации проверок гипотез.
Когда наносимое значение выходит за любую из контрольных границ или серия значений проявляет необычные структуры, (раздел 7), состояние статистической управляемости подвергается сомнению. В этом случае надо исследовать и обнаружить неслучайные (особые) причины, а процесс можно остановить или скорректировать. Как только особые причины найдены и исключены, процесс снова готов к продолжению работы. При возникновении ошибки первого рода можно не найти никакой особой причины. Тогда считают, что выход точки за границы представляет собой достаточно редкое случайное явление при нахождении процесса в статистически управляемом состоянии.
Если контрольную карту процесса строят впервые, то часто оказывается, что процесс статистически неуправляем. Контрольные границы, рассчитанные на основе данных такого процесса, будут иногда приводить к ошибочным заключениям, поскольку они могут оказаться слишком широкими. Следовательно, прежде чем устанавливать постоянные параметры контрольных карт, надо привести процесс в статистически управляемое состояние.
4 Типы контрольных карт
Контрольные карты Шухарта бывают двух основных типов: для количественных и альтернативных данных. Для каждой контрольной карты встречаются две ситуации:
а) стандартные значения не заданы;
б) стандартные значения заданы.
Стандартные значения - значения, установленные в соответствии с некоторыми конкретными требованиями или целями.
4.1 Контрольные карты, для которых не заданы стандартные значения
Цель таких карт - обнаружение отклонений значений характеристик (например,  , R или какой-либо другой статистики), которые вызваны иными причинами, чем те, которые могут быть объяснены только случайностью. Эти контрольные карты основаны целиком на данных самих выборок и используют для обнаружения вариаций, которые обусловлены неслучайными причинами.
4.2 Контрольные карты при наличии заданных стандартных значений
Целью таких карт является определение того, отличаются ли наблюдаемые значения , R или какой-либо другой статистики), которые вызваны иными причинами, чем те, которые могут быть объяснены только случайностью. Эти контрольные карты основаны целиком на данных самих выборок и используют для обнаружения вариаций, которые обусловлены неслучайными причинами.
4.2 Контрольные карты при наличии заданных стандартных значений
Целью таких карт является определение того, отличаются ли наблюдаемые значения  , R и т.п. для нескольких подгрупп (каждая объемом n наблюдений) от соответствующих стандартных значений Х 0 (или m) и т.п. больше, чем можно ожидать при действии только случайных причин. Особенностью карт с заданными стандартными значениями является дополнительное требование, относящееся к положению центра и вариации процесса. Установленные значения могут быть основаны на опыте, полученном при использовании контрольных карт без априорной информации, или на заданных стандартных значениях, а также на экономических показателях, установленных после рассмотрения потребности в услуге и стоимости производства, или указаны в технических требованиях на продукцию.
Предпочтительно, чтобы установленные значения определялись на основе исследования предварительных данных, которые, как предполагается, станут типичными для всех будущих данных. Для эффективного использования контрольных карт стандартные значения должны быть сопоставимы с присущей процессу изменчивостью. Карты, основанные на таких стандартных значениях, особенно полезны для управления процессами и поддержания однородности продукции на желаемом уровне.
4.3 Типы контрольных карт для количественных и качественных признаков
В стандарте рассмотрены следующие контрольные карты:
а) контрольные карты для количественных данных:
1) карты среднего ( , R и т.п. для нескольких подгрупп (каждая объемом n наблюдений) от соответствующих стандартных значений Х 0 (или m) и т.п. больше, чем можно ожидать при действии только случайных причин. Особенностью карт с заданными стандартными значениями является дополнительное требование, относящееся к положению центра и вариации процесса. Установленные значения могут быть основаны на опыте, полученном при использовании контрольных карт без априорной информации, или на заданных стандартных значениях, а также на экономических показателях, установленных после рассмотрения потребности в услуге и стоимости производства, или указаны в технических требованиях на продукцию.
Предпочтительно, чтобы установленные значения определялись на основе исследования предварительных данных, которые, как предполагается, станут типичными для всех будущих данных. Для эффективного использования контрольных карт стандартные значения должны быть сопоставимы с присущей процессу изменчивостью. Карты, основанные на таких стандартных значениях, особенно полезны для управления процессами и поддержания однородности продукции на желаемом уровне.
4.3 Типы контрольных карт для количественных и качественных признаков
В стандарте рассмотрены следующие контрольные карты:
а) контрольные карты для количественных данных:
1) карты среднего (  ) и размахов (R) или выборочных стандартных отклонений (s);
2)карта индивидуальных значений (X) и скользящих размахов (R);
3) карта медиан (Me) и размахов (R);
б) контрольные карты для альтернативных данных:
1) карта долей несоответствующих единиц продукции (р) или карта числа несоответствующих единиц (nр);
2)карта числа несоответствий (с) или карта числа несоответствий, приходящихся на единицу продукции (и).
5 Контрольные карты для количественных данных
Количественные данные представляют собой наблюдения, полученные с помощью измерения и записи значений некоторой характеристики для каждой единицы, рассматриваемой в подгруппе, например длина в метрах, сопротивление в омах, шум в децибелах и т.д. Карты для количественных данных, и особенно простейшие из них ( ) и размахов (R) или выборочных стандартных отклонений (s);
2)карта индивидуальных значений (X) и скользящих размахов (R);
3) карта медиан (Me) и размахов (R);
б) контрольные карты для альтернативных данных:
1) карта долей несоответствующих единиц продукции (р) или карта числа несоответствующих единиц (nр);
2)карта числа несоответствий (с) или карта числа несоответствий, приходящихся на единицу продукции (и).
5 Контрольные карты для количественных данных
Количественные данные представляют собой наблюдения, полученные с помощью измерения и записи значений некоторой характеристики для каждой единицы, рассматриваемой в подгруппе, например длина в метрах, сопротивление в омах, шум в децибелах и т.д. Карты для количественных данных, и особенно простейшие из них (  - и R -карты), - это классические контрольные карты, применяемые для управления процессами.
Контрольные карты для количественных данных имеют следующие преимущества:
а) большинство процессов и их продукция на выходе имеют характеристики, которые могут быть измерены, так что применимость таких карт потенционально широка;
б) измеренное значение содержит больше информации, чем простое утверждение «да - нет»;
в) характеристики процесса могут быть проанализированы безотносительно установленных требований. Карты запускаются вместе с процессом и дают независимую картину того, на что процесс способен. После этого характеристики процесса можно сравнивать или нет с установленными требованиями;
г) хотя получение количественных данных дороже, чем альтернативных, объемы подгрупп для количественных данных почти всегда гораздо меньше и при этом намного эффективнее. Это позволяет в некоторых случаях снизить общую стоимость контроля и уменьшить временной разрыв между производством продукции и корректирующим воздействием.
Для контрольных карт, использующих количественные данные, предполагается нормальное (гауссово) распределение для вариаций внутри выборок, причем отклонения от этого предположения влияют на эффективность карт. Коэффициенты для вычисления контрольных границ выведены при условии нормальности. Поскольку контрольные границы используются только как эмпирические критерии при принятии решений, целесообразно пренебрегать малыми отклонениями от нормальности. Благодаря центральной предельной теореме выборочные средние имеют распределение, приближающееся к нормальному с ростом объема выборки, даже когда отдельные наблюдения не подчиняются нормальному закону. Это обосновывает возможность предположения о нормальности для - и R -карты), - это классические контрольные карты, применяемые для управления процессами.
Контрольные карты для количественных данных имеют следующие преимущества:
а) большинство процессов и их продукция на выходе имеют характеристики, которые могут быть измерены, так что применимость таких карт потенционально широка;
б) измеренное значение содержит больше информации, чем простое утверждение «да - нет»;
в) характеристики процесса могут быть проанализированы безотносительно установленных требований. Карты запускаются вместе с процессом и дают независимую картину того, на что процесс способен. После этого характеристики процесса можно сравнивать или нет с установленными требованиями;
г) хотя получение количественных данных дороже, чем альтернативных, объемы подгрупп для количественных данных почти всегда гораздо меньше и при этом намного эффективнее. Это позволяет в некоторых случаях снизить общую стоимость контроля и уменьшить временной разрыв между производством продукции и корректирующим воздействием.
Для контрольных карт, использующих количественные данные, предполагается нормальное (гауссово) распределение для вариаций внутри выборок, причем отклонения от этого предположения влияют на эффективность карт. Коэффициенты для вычисления контрольных границ выведены при условии нормальности. Поскольку контрольные границы используются только как эмпирические критерии при принятии решений, целесообразно пренебрегать малыми отклонениями от нормальности. Благодаря центральной предельной теореме выборочные средние имеют распределение, приближающееся к нормальному с ростом объема выборки, даже когда отдельные наблюдения не подчиняются нормальному закону. Это обосновывает возможность предположения о нормальности для  -карт даже при объемах выборок, столь малых как 4 или 5 единиц, взятых для проведения контроля. Если используют отдельные наблюдения для изучения возможностей процесса, истинное распределение важно. Рекомендуется периодически перепроверять выполнение таких предположений, чтобы убедиться, что используемые данные принадлежат одной совокупности. Распределения размахов и стандартных отклонений отличаются от нормального, хотя предположение нормальности использовалось при оценке коэффициентов для вычисления контрольных границ. Такие границы, как правило, приемлемы для процедур принятия эмпирических решений.
5.1 Карты средних ( -карт даже при объемах выборок, столь малых как 4 или 5 единиц, взятых для проведения контроля. Если используют отдельные наблюдения для изучения возможностей процесса, истинное распределение важно. Рекомендуется периодически перепроверять выполнение таких предположений, чтобы убедиться, что используемые данные принадлежат одной совокупности. Распределения размахов и стандартных отклонений отличаются от нормального, хотя предположение нормальности использовалось при оценке коэффициентов для вычисления контрольных границ. Такие границы, как правило, приемлемы для процедур принятия эмпирических решений.
5.1 Карты средних ( ) и размахов (R) или выборочных стандартных отклонений (s)
Карты для количественных данных отражают состояние процесса через разброс (изменчивость от единицы к единице) и через расположение центра (среднее процесса). Поэтому контрольные карты для количественных данных почти всегда применяют и анализируют парами - одна карта для расположения и одна - для разброса. Наиболее часто используют пару ) и размахов (R) или выборочных стандартных отклонений (s)
Карты для количественных данных отражают состояние процесса через разброс (изменчивость от единицы к единице) и через расположение центра (среднее процесса). Поэтому контрольные карты для количественных данных почти всегда применяют и анализируют парами - одна карта для расположения и одна - для разброса. Наиболее часто используют пару  - и R -карту. В таблицах 1 и 2 приведены формулы контрольных границ и коэффициенты для соответствующих карт.
Таблица 1 - Формулы контрольных границ для карт Шухарта с использованием количественных данных - и R -карту. В таблицах 1 и 2 приведены формулы контрольных границ и коэффициенты для соответствующих карт.
Таблица 1 - Формулы контрольных границ для карт Шухарта с использованием количественных данных
Таблица 2 - Коэффициенты для вычисления линий контрольных карт
5.2 Контрольные карты индивидуальных значений (X) В некоторых ситуациях для управления процессами невозможно либо непрактично иметь дело с рациональными подгруппами. Время или стоимость, требуемые для измерения при одиночном наблюдении, столь велики, что проведение повторных наблюдений даже не рассматривают. Это обычно происходит, когда измерения дорогостоящие (например при разрушающем контроле) или выход продукции все время относительно однороден. В других ситуациях нельзя получить более одного значения, например показание прибора или значение характеристики партии исходных материалов, поэтому приходится управлять процессом на основе индивидуальных значений. При использовании карт индивидуальных значений рациональные подгруппы для обеспечения оценки изменчивости внутри партии не применяют и контрольные границы рассчитывают на основе меры вариации, полученной по скользящим размахам обычно двух наблюдений. Скользящий размах - это абсолютное значение разности измерений в последовательных парах, т.е. разность первого и второго измерений, затем второго и третьего и т.д. На основе скользящих размахов вычисляют средний скользящий размах Таблица 3 - Формулы контрольных границ для карт индивидуальных значений
При использовании карт индивидуальных значений необходимо учитывать следующее: а) карты индивидуальных значений не столь чувствительны к изменениям процесса, как б) при интерпретации карт индивидуальных значений следует проявлять осторожность, если распределение процесса не является нормальным; в) карты индивидуальных значений не оценивают повторяемость процесса от изделия к изделию, и поэтому в некоторых случаях лучше использовать обычные 5.3 Контрольные карты медиан (Me) Карты медиан - альтернатива Контрольные границы для карт медиан вычисляют двумя способами: посредством расчета медиан от медиан подгрупп и медиан размахов или расчета средних от медиан подгрупп и средних размахов. Последний способ проще и удобнее (5.3.1 и 5.3.2). 5.3.1 Карта медиан Центральная линия равна Карту медиан строят таким же образом, как и Таблица 4 - Значения коэффициента А4
Следует отметить, что карта медиан с границами 3s более медленно реагирует на выход процесса из состояния статистической управляемости, чем 5.3.2 Карта размахов Центральная линия равна Значения постоянных D 3 и D 4 приведены в таблице 2. |
Метод управления и интерпретация контрольных карт для количественных данных
Система карт Шухарта опирается на следующее условие: если изменчивость процесса от единицы к единице и среднее процесса остаются постоянными на данных уровнях (оцененные, соответственно, по  и
и 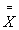 ),то размахи R и средние
),то размахи R и средние  отдельных подгрупп будут меняться только случайным образом и редко выходить за контрольные границы. Не допускаются очевидные тренды или структуры данных, кроме возникающих случайно с некоторой долей вероятности.
отдельных подгрупп будут меняться только случайным образом и редко выходить за контрольные границы. Не допускаются очевидные тренды или структуры данных, кроме возникающих случайно с некоторой долей вероятности.
 -карта показывает, где находится среднее процесса и какова его стабильность. Та же карта выявляет нежелательные вариации между подгруппами и вариации относительно их среднего. R -карта выявляет любую нежелательную вариацию внутри подгрупп и служит индикатором изменчивости исследуемого процесса. Это мера состоятельности и однородности процесса. Если R -карта показывает, что вариации внутри подгрупп не изменяются, то это значит, что процесс остается в статистически управляемом состоянии. Такое происходит только в том случае, если все выборки обрабатывались одинаково. Если R -карта показывает, что процесс вышел из управляемого состояния или уровень на R -карте возрастает, то это может означать, что либо отдельные подгруппы подверглись разной обработке, либо в процессе действует несколько различных систем причинно-следственных связей.
-карта показывает, где находится среднее процесса и какова его стабильность. Та же карта выявляет нежелательные вариации между подгруппами и вариации относительно их среднего. R -карта выявляет любую нежелательную вариацию внутри подгрупп и служит индикатором изменчивости исследуемого процесса. Это мера состоятельности и однородности процесса. Если R -карта показывает, что вариации внутри подгрупп не изменяются, то это значит, что процесс остается в статистически управляемом состоянии. Такое происходит только в том случае, если все выборки обрабатывались одинаково. Если R -карта показывает, что процесс вышел из управляемого состояния или уровень на R -карте возрастает, то это может означать, что либо отдельные подгруппы подверглись разной обработке, либо в процессе действует несколько различных систем причинно-следственных связей.
На  -карты также могут повлиять условия, при которых процесс вышел из состояния статистической управляемости по R -карте. Возможность интерпретировать размахи или средние подгрупп зависит от оценки изменчивости от единицы к единице, поэтому R -карту необходимо анализировать первой. Процедура управления приведена в 6.1 - 6.7.
-карты также могут повлиять условия, при которых процесс вышел из состояния статистической управляемости по R -карте. Возможность интерпретировать размахи или средние подгрупп зависит от оценки изменчивости от единицы к единице, поэтому R -карту необходимо анализировать первой. Процедура управления приведена в 6.1 - 6.7.
6.1 Собирают и анализируют данные, вычисляют средние и размахи.
6.2 Строят R -карту. Сопоставляют нанесенные точки размахов с контрольными границами, выделяют точки вне границ, необычные структуры или тренды. Для каждого сигнала о наличии неслучайной причины в значениях размаха проводят анализ операций процесса, чтобы определить причину. Проводят корректирующие действия и действия по предотвращению повторения данной причины.
6.3. Исключают все подгруппы, на которые повлияла неслучайная причина, затем пересчитывают и наносят на карту новые средний размах  и контрольные границы. Необходимо получить подтверждение того, что все точки размахов при сравнении с новыми границами указывают на статистическую управляемость. Если требуется, повторяют последовательность действий «идентификация - корректировка - пересчет».
и контрольные границы. Необходимо получить подтверждение того, что все точки размахов при сравнении с новыми границами указывают на статистическую управляемость. Если требуется, повторяют последовательность действий «идентификация - корректировка - пересчет».
6.4. Если некоторые подгруппы исключены из R -карты из-за выявленных особых причин, их надо исключить и из  -карты. Пересмотренные значения
-карты. Пересмотренные значения  и
и 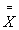 надо использовать для пересчета пробных контрольных границ для средних
надо использовать для пересчета пробных контрольных границ для средних  .
.
Примечание - Исключение подгрупп, представляющих причину выхода процесса из состояния статистической управляемости, это не «исключение плохих данных». Скорее, здесь исключаются точки, на которые повлияли известные неслучайные причины, и мы получаем лучшую оценку основного уровня изменчивости из-за случайных причин. Это дает наиболее подходящую основу для контрольных границ, применение которых позволяет наиболее эффективным образом обнаруживать будущие проявления неслучайных причин вариаций.
6.5. Когда размахи находятся в статистически управляемом состоянии, разброс процесса (отклонения внутри подгрупп) считается стабильным. В этом случае можно проанализировать средние, чтобы увидеть, меняется ли со временем среднее положение процесса.
6.6. Теперь строят  -карту и сравнивают точки с контрольными границами. Выделяют точки вне границ, необычные структуры точек или тренды. Также как и для R -карты необходимо анализировать любое из состояний статистической неуправляемости и проводить корректирующие и превентивные меры. Надо исключить точки, которые характеризуют это состояние и для которых были найдены неслучайные причины.
-карту и сравнивают точки с контрольными границами. Выделяют точки вне границ, необычные структуры точек или тренды. Также как и для R -карты необходимо анализировать любое из состояний статистической неуправляемости и проводить корректирующие и превентивные меры. Надо исключить точки, которые характеризуют это состояние и для которых были найдены неслучайные причины.
Повторно вычисляют и наносят на график новое среднее процесса (  ) и контрольные границы. Проверяют, чтобы, по сравнению с новыми границами, все точки демонстрировали статистически управляемое состояние, при необходимости возобновляя последовательные действия: «идентификация - корректировка - пересчет».
) и контрольные границы. Проверяют, чтобы, по сравнению с новыми границами, все точки демонстрировали статистически управляемое состояние, при необходимости возобновляя последовательные действия: «идентификация - корректировка - пересчет».
6.7. Если исходные данные для установления эталонных значений контрольных границ располагаются устойчиво внутри пробных пределов, расширяют границы, чтобы охватить будущие данные. Исполнители (оператор или (и) мастер) должны пользоваться этими границами для последующего управления процессом, реагировать на сигналы о выходе процесса из управляемого состояния на любой из  и R- карт и выполнять надлежащие действия.
и R- карт и выполнять надлежащие действия.
|
|
|



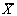

 или
или