 |
Примеры контрольных карт для количественных данных
|
|
|
|
12.1 
- и R -карты. Стандартные значения заданы
Менеджер по качеству импортера чая на основании подобных процессов предъявляет требования к процессу упаковки такие, чтобы средний вес упаковки был 100,6 г и предполагаемое стандартное отклонение процесса равно 1,4 г. - получено на основе аналогичных упаковочных процессов.
Поскольку стандартные значения даны (Х 0 = 100,6; s0 = 1,4), контрольную карту средних и карту размахов можно построить с использованием формул, приведенных в таблице 1 и коэффициентов А, d2, D 2 и D 1, приведенных в таблице 2 для n = 5.
-КАРТА:
центральная линия: Х 0 = 100,6 г
UCL = Х 0 + Аs 0 = 100,6 + (1,342 · 1,4) = 102,5 г
LCL = Х 0 - А s0 =100,6 - (1,342 · 1,4) = 98,7 г
R -КАРТА:
центральная линия: d 2 s 0 =2,326 · 1,4 = 3,3 г
UCL = D 20 = 4,918 · 1,4 = 6,9 г
LCL = D 1s0 = 0 · 1,4 = 0
(т.к. n < 7, то LCL отсутствует)
Для контроля следует взять 25 выборок объема 5. Значения их средних и размахов приведены в таблице 6. На рисунке 5 они нанесены вместе с контрольными границами.
Таблица 6 - Процесс упаковки чая
| Номер подгруппы | Среднее подгруппы 
| Размах подгруппы R |
| 100,6 | 3,4 | |
| 101,3 | 4,0 | |
| 99,6 | 2,2 | |
| 100,5 | 4,5 | |
| 99,9 | 4,8 | |
| 99,5 | 3,8 | |
| 100,4 | 4,1 | |
| 100,5 | 1,7 | |
| 101,1 | 2,2 | |
| 100,3 | 4,6 | |
| 100,1 | 5,0 | |
| 99,6 | 6,1 | |
| 99,2 | 3,5 | |
| 99,4 | 5,1 | |
| 99,4 | 4,5 | |
| 99,6 | 4,1 | |
| 99,3 | 4,7 | |
| 99,9 | 5,0 | |
| 100,5 | 3,9 | |
| 99,5 | 4,7 | |
| 100,1 | 4,6 | |
| 100,4 | 4,4 | |
| 101,1 | 4,9 | |
| 99,9 | 4,7 | |
| 99,7 | 3,4 |
Рисунок 5 - Карты средних и размахов по данным таблицы 6
Карты, изображенные на рисунке 5, показывают, что процесс не находится в статистически управляемом состоянии на требуемом уровне, так как есть последовательность из 20 точек, лежащих ниже центральной линии на -карте и последовательность из 21 точек выше центральной линии на R -карте. Причина столь длинной последовательности низких значений среднего должна быть исследована и устранена.
|
|
|
12.2 - и R -карты. Стандартные значения не заданы
В таблице 7 приведены результаты измерений внешнего радиуса втулки. Каждые полчаса делалось четыре измерения, всего взято 20 выборок. Средние и размахи подгрупп также приведены в таблице 7. Установлены предельно допустимые значения внешнего радиуса: 0,219 и 0,125 дм. Цель - определение показателей процесса и управление им по настройке и разбросу так, чтобы он соответствовал установленным требованиям.
Таблица 7 - Производственные данные для внешнего радиуса втулки
| Номер подгруппы | Радиус | Среднее 
| Размах R | |||
| х1 | х2 | х3 | х4 | |||
| 0,1898 | 0,1729 | 0,2067 | 0,1898 | 0,1898 | 0,0338 | |
| 0,2012 | 0,1913 | 0,1878 | 0,1921 | 0,1931 | 0,0134 | |
| 0,2217 | 0,2192 | 0,2078 | 0,1980 | 0,2117 | 0,0237 | |
| 0,1832 | 0,1812 | 0,1963 | 0,1800 | 0,1852 | 0,0163 | |
| 0,1692 | 0,2263 | 0,2066 | 0,2091 | 0,2033 | 0,0571 | |
| 0,1621 | 0,1832 | 0,1914 | 0,1783 | 0,1788 | 0,0293 | |
| 0,2001 | 0,1937 | 0,2169 | 0,2082 | 0,2045 | 0,0242 | |
| 0,2401 | 0,1825 | 0,1910 | 0,2264 | 0,2100 | 0,0576 | |
| 0,1996 | 0,1980 | 0,2076 | 0,2023 | 0,2019 | 0,0096 | |
| 0,1783 | 0,1715 | 0,1829 | 0,1961 | 0,1822 | 0,0246 | |
| 0,2166 | 0,1748 | 0,1960 | 0,1923 | 0,1949 | 0,0418 | |
| 0,1924 | 0,1984 | 0,2377 | 0,2003 | 0,2072 | 0,0453 | |
| 0,1768 | 0,1986 | 0,2241 | 0,2022 | 0,2004 | 0,0473 | |
| 0,1923 | 0,1876 | 0,1903 | 0,1986 | 0,1922 | 0,0110 | |
| 0,1924 | 0,1996 | 0,2120 | 0,2160 | 0,2050 | 0,0236 | |
| 0,1720 | 0,1940 | 0,2116 | 0,2320 | 0,2049 | 0,0600 | |
| 0,1824 | 0,1790 | 0,1876 | 0,1821 | 0,1828 | 0,0086 | |
| 0,1812 | 0,1585 | 0,1699 | 0,1680 | 0,1694 | 0,0227 | |
| 0,1700 | 0,1567 | 0,1694 | 0,1702 | 0,1666 | 0,0135 | |
| 0,1698 | 0,1664 | 0,1700 | 0,1600 | 0,1655 | 0,0100 |
где k - число подгрупп, k = 20.
Первый шаг: построение R -карты и определение по ней состояния процесса.
R -КАРТА:
центральная линия: 
(т.к. n <7, то LCL отсутствует).
Значения множителей D 3 и D 4 взяты из таблицы 2 для n = 4. Поскольку значения 
в таблице 7 находятся внутри контрольных границ, 
-карта указывает на статистически управляемое состояние. Значение теперь может быть использовано для вычисления контрольных границ -карты.
|
|
|
-КАРТА.
Центральная линия: 
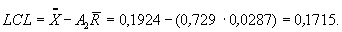
Значение множителя А 2 берется из таблицы 2 для n = 4.
- и R -карты представлены на рисунке 6. Анализ -карты показывает, что последние три точки вышли за границы. Это указывает на возможность действия некоторых особых причин вариаций. Если пределы были вычислены на основе предыдущих данных, то должно быть предпринято действие в точке, соответствующей 18-й подгруппе.
Рисунок 6 - Карты средних и размахов по данным таблицы 7
В этой точке процесса следует произвести соответствующее корректирующее действие, чтобы устранить особые причины и предотвратить их повторение. Работа с картами продолжается после установления пересмотренных контрольных границ без исключенных точек, которые вышли за старые границы, т.е. значений для выборок № 18, 19 и 20. Значения 
, 
и линии контрольной карты пересчитывают следующим образом:
пересмотренное значение 
пересмотренное значение 
пересмотренная -карта имеет следующие параметры:
центральная линия: 
пересмотренная R -карта:
центральная линия: 
(т.к. n <7, то LCL отсутствует).
Рисунок 7 - Пересмотренные - и 
-карты по данным таблицы 7
Для стабильного процесса с пересмотренными контрольными границами можно оценить возможности. Вычисляем индекс возможностей:
где 
оценивается как 
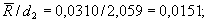
значение постоянной d 2 берется из таблицы 2 для n = 4.
Таким образом,
Поскольку PCI больше 1, возможности процесса можно считать приемлемыми. Однако при тщательном изучении можно увидеть, что процесс не настроен правильно относительно допуска и поэтому около 11,8 % единиц будут выходить за установленное верхнее предельно допустимое значение UTL. Поэтому, прежде чем установить постоянные параметры контрольных карт, надо попытаться правильно настроить процесс, поддерживая его при этом в статистически управляемом состоянии.
12.3 Контрольные карты для индивидуальных значений X и скользящих размахов R. Стандартные значения не заданы
В таблице 8 представлены результаты лабораторного анализа влажности сухого молока, проведенного по выборкам из 10 последовательных партий. Выборку сухого молока, представляющую партию, анализируют в лаборатории по таким характеристикам, как жирность, влажность, кислотность, индекс растворимости, оборудование, осадки, бактерии и сывороточный протеин. Было намечено поддерживать для этого процесса процент влажности ниже 4 %. Вариации влажности внутри одной партии оказались пренебрежимо малыми, так что было решено брать только одно наблюдение из партии и установить контрольные границы на основе скользящего размаха последовательности партий.
|
|
|
Таблица 8 - Процент влажности для 10 последовательных выборок молочного порошка
| Наименование показателя | Значение для подгруппы | |||||||||
| Влажность X, % | 2,9 | 3,2 | 3,6 | 4,3 | 3,8 | 3,5 | 3,0 | 3,1 | 3,6 | 3,5 |
| Скользящий размах R | 0,3 | 0,4 | 0,7 | 0,5 | 0,3 | 0,5 | 0,1 | 0,5 | 0,1 |
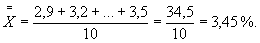
Линии контрольной карты для скользящих размахов R:
центральная линия 
(т.к. n <7, то LCL отсутствует).
Значения множителей D 3 и D 4 берутся из таблицы 2 для n = 2. Поскольку карта размахов демонстрирует статистически управляемое состояние, можно построить контрольную карту индивидуальных значений.
Линии контрольной карты индивидуальных значений X:
центральная линия: 
Формулы для контрольных границ и значение коэффициента Е 2 даны в таблицах 3, 4. Контрольные карты приведены на рисунке 8. Они показывают, что процесс находится в состоянии статистической управляемости.
Рисунок 8 - Контрольная карта индивидуальных значений X по данным, приведенным в таблице 8
12.4 Карта медиан. Стандартные значения не заданы
Станок производит электронные диски с заданной толщиной от 0,007 до 0,016 см. Выборки объема 5 единиц берут каждые полчаса, и толщину дисков записывают, как показано в таблице 9.
Таблица 9 - Данные контроля толщины слюдяных дисков (значения мкм)
| Номер подгруппы | Толщина | Медиана Me | Размах R | ||||
| Х 1 | Х 2 | Х 3 | Х 4 | Х 5 | |||
Было решено использовать для управления качеством продукции карту медиан. Значения медиан и размахов также даны в таблице 9.
|
|
|
Вычисляем среднее медиан подгрупп и размахов следующим образом:
R-карта:
центральная линия 
(т.к. n <7, то LCL отсутствует).
Значения постоянных D 3 и D 4 берутся из таблицы 2 при n = 5. Поскольку карта размахов показывает статистически управляемое состояние, можно вычислить линии контрольных границ карты медиан.
Карта медиан:
центральная линия: 
Значение А 4 берется из таблицы 4 при n = 5. Графики построены на рисунке 9. Как видно из карт, процесс показывает состояние статистической управляемости.
Рисунок 9 - Карты медиан и размахов по данным таблицы 9
|
|
|
