 |
Лабораторная работа выполняется на стенде ТМЖ-2В-09-12
|
|
|
|
Сложный трубопровод состоит из трех последовательно соединенных прозрачных труб из органического стекла с внутренними диаметрами dI = 15 мм, dII = 11 мм, dIII = 15 мм. Расстояния между точками отбора и схему подключения пьезометров см. рис. 1.
Для исследования влияния изменений геометрического напора конструкцией стенда предусмотрена возможность изменения угла наклона оси трубопровода к горизонту.
Переходы между участками трубопровода выполнены в виде конусов (конфузора и диффузора).
1. Полностью закрыть задвижки З1, З2, З4, З5, З6, З7, З8 и краны КР4, КР5, КР8, КР12. Краны КР6, КР7, КР9, КР14 полностью открыть.
2. Повернуть переключатель насоса НЗ в крайнее правое положение и включить питание переключением соответствующего тумблера на блоке управления.
3. Дождаться наполнения напорной секции накопительного бака, вплоть до возникновения перелива.
4. Откручивая рукоятку задвижки З6 установить уровень жидкости в пьезометре №12 (НП12) в соответствии с табл. 3.1.
5. Закрыть кран КР9. Измерить время Δt заполнения объема V жидкости, поступающей в мерную емкость ЕМ1. Записать значения в таблицу 3.1. Открыть кран КР9.
6. Записать в таблицу 3.1. показания пьезометров №13, 14, 15, 16, 17 (НП13,НП14, НП15, НП16, НП17).
7. Повторить действия, описанные в пунктах 4, 5 и 6 для всего интервала НП12 из табл. 3.1. Результаты замеров записать в табл. 3.1.
8. Изменяя угол наклона трубопровода ТЗ (контролируется по специальной линейке, размещенной на кронштейне трубопровода) при неизменной величине перекрытия задвижки З6 (рекомендуется перекрытие около 5 оборотов рукоятки задвижки), повторить измерения до пункта 8. Результаты записать в таблицу 3.2. Чтобы изменить угол наклона трубопровода ТЗ следует ослабить барашек винтового фиксатора, расположенный на тыльной стороне пластины кронштейна, придерживая поворотный механизм за металлическую прямоугольную трубу, к которой крепится прозрачный трубопровод.
|
|
|
9. Полностью закрыть задвижку З6.
10. Выключить питание насоса.
Обработка результатов опыта:
1. Рассчитать величину подачи  насоса и записать значения в
насоса и записать значения в
таблицу 3.1.
2. Рассчитать потери статического напора по длине участков трубопровода  ;
;  ;
;  .
.
3. Рассчитать местные потери пьезометрического напора:
а) В плавном сужении русла (конфузоре)  ;
;
б) В плавном расширении (диффузоре) 
4. Рассчитать средние скорости жидкости и критерии Рейнольдса для каждого участка по формулам:


 ,
, 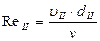 ,
,  ,
,
где SI, SII – площади сечений соответствующих участков трубопровода;
ν – кинематическая вязкость жидкости (для воды при нормальных условиях ν = 10-6 м2/с = 12 мм2/с).
5. Определить коэффициенты Кориолиса, используя число Рейнольдса и данные в теоретической части лабораторной работы.
6. Рассчитать скоростные напоры на каждом участке трубопровода:
 ,
,  ,
,  .
.
7. Рассчитать суммарные пьезометрические напоры для каждого участка:
 ,
,
 ,
,
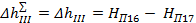 .
.
Потребный пьезометрический напор сложного трубопровода:
 .
.
8. Рассчитать потребные полные напоры участков и трубопровода в целом.
 ,
,
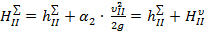 ,
,
 .
.
Полный напор сложного трубопровода с последовательным соединением:
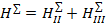 .
.
9. Построить характеристики для участков трубопровода  ,
,  ,
, 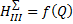 , общую характеристику сложного трубопровода с последовательным соединением участков в координатах подача - потребный напор
, общую характеристику сложного трубопровода с последовательным соединением участков в координатах подача - потребный напор 
10. При одном фиксированном значении расхода через трубопровод (рекомендуется при максимальном) построить линии пьезометрического напора, дополнив его линиями скоростных напоров, и получить линию полного напора. Линию пьезометрических напоров следует строить по показаниям пьезометров. Линия полного напора получается при увеличении линии пьезометрического напора на величину скоростного напора.
|
|
|
Схематичный пример построения пьезометрической и напорной линий показан на рис. 5.
11. Сделать и записать выводы.
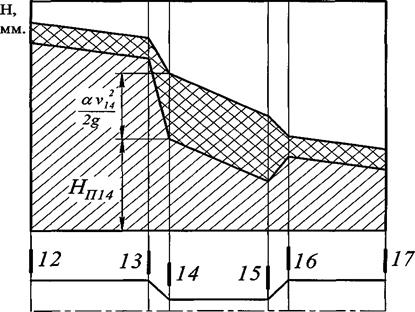
Рис. 5. Пьезометрическая и напорная линии.
Таблица 3.1
| № | V, л. | Δt, сек. | Q, л/с. | НП12, мм. | НП13, мм. | НП14, мм. | НП15, мм. | НП16, мм. | НП17, мм. | υI, мм/с. | υII, мм/с. | υIII, мм/с. | ReI | ReII | ReIII |
Таблица 3.1 (продолжение)
| № | ΔhI, мм. | ΔhII, мм. | ΔhIII, мм. | Δh1314, мм. | Δh1516, мм. | Δh910, мм. |  , мм. , мм.
|  , мм. , мм.
|  , мм. , мм.
|  , мм. , мм.
| 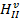 , мм. , мм.
|  , мм. , мм.
|  , мм. , мм.
| 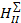 , мм. , мм.
|  , мм. , мм.
|  , мм. , мм.
|
Таблица 3. 2
| № | Угол наклона к горизонту ТЗ | V, л. | Δt, сек. | Q л/с. | НП12, мм. | НП13, мм. | НП14, мм. | НП15, мм. | НП16, мм. | НП17, мм. |
| -1 | ||||||||||
| -3 |
ЛАБОРАТОРНАЯ РАБОТА №4
Исследование характеристик трубопроводов при различных режимах течения
Цель работы:
Закрепление знаний по разделам "Ламинарное и турбулентное течение в круглых трубах", получение навыков экспериментального определения характеристик трубопровода.
|
|
|
Задание:
Определить из опыта коэффициент гидравлического трения λ при заданном расходе в имеющемся трубопроводе. Сравнить полученную величину λ с величиной, определенной по справочным данным.
Теоретические основы метода:
Потери напора h на участке трубопровода в общем случае определяются из уравнения Бернулли:
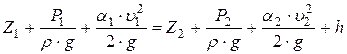
| (4.1) |
где Z1 – геометрическая высота сечения 1-1;
Z2 – геометрическая высота сечения 2-2;
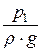 – пьезометрический напор в сечении 1-1;
– пьезометрический напор в сечении 1-1;
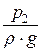 – пьезометрический напор в сечении 2-2;
– пьезометрический напор в сечении 2-2;
υ1 – средняя скорость потока в сечении 1-1;
υ2 – средняя скорость потока в сечении 2-2;
α1 – коэффициент Кориолиса в сечение 1-1;
α2 – коэффициент Кориолиса в сечение 2-2;
Исследуемый участок трубопровода представляет собой отрезок прямой горизонтальной трубы постоянного диаметра, поэтому потери на трение являются единственным видом потерь напора на этом участке. Кроме того, Z1 = Z2 и υ1 = υ2, а значит и α1 = α2, поэтому из уравнения (4.1) следует, что потери на трение на исследуемом участке:

| (4.2) |
Потери напора на трение в общем случае определяются по формуле Дарси:

| (4.3) |
Коэффициент λ называют коэффициентом гидравлического трения. Исследования показали, что для ламинарных потоков в трубах:

| (4.4) |
где А – константа, зависящая от формы сечения трубопровода. Для круглой трубы А = 64, а число Рейнольдса определяется по формуле:

| (4.5) |
При турбулентных режимах λ зависит от конфигурации потока или, как говорят, от пограничной геометрии, а также от числа Рейнольдса:

| (4.6) |
По результатам экспериментов коэффициент λ можно определить с помощью формулы (4.3), если измерить среднюю скорость υ и потери напора hтр.
Теоретические исследования показали, что согласно (4.6) следует искать эмпирическую зависимость λ от числа Re икакого-либо безразмерного параметра, определяющего геометрическое подобия потоков. Для гладких круглых труб такого параметра не требуется, поскольку все круглые трубы геометрически подобны и для них экспериментальные точки на графике λ=λ(Re) должны образовать единую кривую. Однако шероховатые трубы не являются геометрически подобными, поскольку требование геометрического подобия должно распространяться не только на форму поперечного сечения, но и на форму выступов неровностей стенок. Но тогда при строгом подходе практически невозможно найти две геометрически подобные трубы с естественной шероховатостью. В связи с этим в качестве приближенного допущения принимают, что шероховатые трубы будут геометрически подобными, если отношение средней высоты выступов шероховатости Δ к радиусу ro или диаметру d будет одинаковым. Тогда опытные данные следует обрабатывать в виде кривых:
|
|
|

| (4.7) |
Отношение Δ/d (или Δ/r0) называют относительной шероховатостью, а обратную величину d/Δ – относительно гладкостью.
Н. Никурадзе (1933 г.) впервые обработал свои многочисленные опытные результаты указанным способом и построил универсальный график зависимости (4.7) приведенный на рисунке 6. Шероховатость в опытах Никурадзе создавалась искусственно путем наклеивания калиброванных песчинок на внутреннюю поверхность трубы. Такая шероховатость получалась равнозернистой, чем существенно отличалась от естественной шероховатости труб, образующейся в результате коррозии, отложений и т.п.
Рассмотрим подробно график Никурадзе:
1 - зона ламинарного режима, изображенная прямой. Здесь точки, относящиеся к опытам с разной шероховатостью, ложатся на одну прямую, уравнением которой является зависимость:

| (4.8) |

|
Границей служит значение абсциссы lg(2300) = lg(Reкр).
Таким образом, данная закономерность имеет место при Re ≤ Reкр, т.е. при ламинарном режиме движения.
В диапазоне чисел Re = 2300¸4000 осуществляется переход от ламинарного течения к турбулентному. В потоке наблюдается неустойчивость, порождаемая периодическим возникновением очагов турбулентности и их исчезновением.
2 - зона гладкостенного течения, образуемая опытными точками, расположенными вдоль другой прямой. Здесь λ также не зависит от шероховатости:

| (4.9) |
Границей зоны ориентировочно могут служить значения:

| (4.10) |
Строение потока в пределах гладкостенной зоны можно представить в виде: турбулентного ядра потока и вязкого подслоя вблизи стенки, движения в котором преимущественно ламинарное. Толщина подслоя δл достаточна, чтобы покрыть все неровности стенки, благодаря чему движение турбулентного ядра потока происходит как бы в гладкой трубе. Трубы, работающие в таком режиме, называют гидравлически гладкими.
|
|
|
3 - доквадратичная зона сопротивления, которая ограничивается линией гладкостенного режима и штриховой линией К-К, образованной точками, отделяющими горизонтальные участки кривых. В зоне 3 каждая кривая отвечает определенному значению относительной гладкости. Здесь λ зависит от числа Rе и относительной гладкости трубы d/Δ:

| (4.11) |
Границами зоны приближенно служат значения:
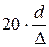 <Re <Re  . .
| (4.12) |
4 - зона квадратичного сопротивления, образуемая горизонтальными участками кривых. В этой зоне коэффициент λ не зависит от Rе,т.е.:

| (4.13) |
Эта зона имеет место при:
Re> 
| (4.14) |
Толщина вязкого подслоя здесь весьма мала, и выступы шероховатости полностью взаимодействуют с турбулентным ядром потока.
График Никурадзе дает общее представление о характере зависимости  для труб с искусственной зернистой шероховатостью Δ.
для труб с искусственной зернистой шероховатостью Δ.
В таблице 4.1 даны удобные для практического использования расчетные формулы коэффициента λ во всех зонах сопротивления.
Таблица 4.1.
| Зона сопротивления | Режим течения | Границы зоны | Расчетные формулы | |
| Ламинарный | Re<2320 | 
| ||
| Турбулентный гладкостенный | 
| 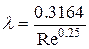 (Re<105)
(Re<105)

| Для всех турбулентных режимов
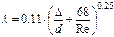
| |
| Турбулентный доквадратичный | 
| 
| ||
| Турбулентный квадратичный | 
| 
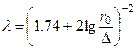
|
Проведение опыта:
|
|
|



 ) от Re для труб с искусственной шерховатостью, построенная Н. Никурадзе.
) от Re для труб с искусственной шерховатостью, построенная Н. Никурадзе.