 |
Контрольная работа Степенная функция
|
|
|
|
Цели: выявление знаний и проверка степени усвоения ими изученного материала; развитие навыков самостоятельной работы.
В а р и а н т I
1. Найдите наибольшее и наименьшее значения функции у = х 6на отрезке [–1; 2].
2. Сколько корней имеет уравнение –0,5 х 4= х – 4?
3. Постройте и прочитайте график функции:

| 4. Найдите наибольшее и наименьшее значения функции у = (х – 2)3+ + 4 на отрезке [0; 3]. |
5. Дана функция f (х), где f (х) = х –3. Найдите все значения х, при которых выполняется неравенство 
В а р и а н т II
1. Найдите наибольшее и наименьшее значения функции у = х 8на отрезке [–2; 1].
2. Сколько корней имеет уравнение 0,5 х 3= 2 – х?
3. Постройте и прочитайте график функции:
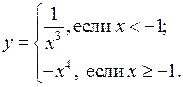
| 4. Найдите наибольшее и наименьшее значения функции у = (х + 3)4– – 4 на отрезке [–4; –1]. |
5. Дана функция f (х), где f (х) = х –5. Найдите все значения х, при которых выполняется неравенство 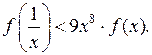
В а р и а н т III
1. Найдите наибольшее и наименьшее значения функции у = х 8на отрезке [–1; 2].
2. Сколько корней имеет уравнение 2 х 4= х – 3?
3. Постройте и прочитайте график функции:
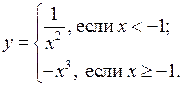
| 4. Найдите наибольшее и наименьшее значения функции у = (х + 3)3– – 1 на отрезке [–4; –1]. |
5. Дана функция f (х), где f (х) = х –4. Найдите все значения х, при которых выполняется неравенство 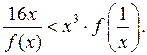
В а р и а н т IV
1. Найдите наибольшее и наименьшее значения функции у = х 6на отрезке [–2; 1].
2. Сколько корней имеет уравнение –0,5 х 3= х – 3?
3. Постройте и прочитайте график функции:
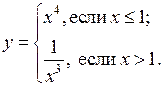
| 4. Найдите наибольшее и наименьшее значения функции у = (х – 2)4– – 1 на отрезке [1; 4]. |
5. Дана функция f (х), где f (х) = х –6. Найдите все значения х, при которых выполняется неравенство 
Контрольная работа Прогрессии
Цели: выявить степень усвоения учащимися изученного материала; развитие навыков самостоятельной работы.
|
|
|
Ход урока
I. Организация учащихся на выполнение работы.
II. Выполнение работы по вариантам.
В а р и а н т I
1. Найдите десятый член арифметической прогрессии –8; –6,5; –5; …. Вычислите сумму первых десяти ее членов.
2. Найдите восьмой член геометрической прогрессии  …
…
3. Сумма третьего и шестого членов арифметической прогрессии равна 3. Второй ее член на 15 больше седьмого. Найдите первый и второй члены этой прогрессии.
4. Найдите все значения х, при которых значения выражений 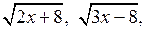 1 являются тремя последовательными членами геометрической прогрессии. 1 являются тремя последовательными членами геометрической прогрессии.
|
5. Найдите сумму всех трехзначных чисел от 100 до 550, которые при делении на 7 дают в остатке 5.
В а р и а н т II
1. Найдите двенадцатый член арифметической прогрессии 26; 23; 20; …. Вычислите сумму первых двенадцати ее членов.
2. Найдите восьмой член геометрической прогрессии 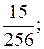
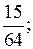
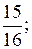 …
…
3. Третий член арифметической прогрессии на 12 меньше шестого. Сумма восьмого и второго членов равна 4. Найдите второй и третий члены этой прогрессии.
4. Найдите все значения х, при которых значения выражений 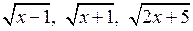 являются тремя последовательными членами геометрической прогрессии. являются тремя последовательными членами геометрической прогрессии.
|
5. Найдите сумму всех двузначных чисел, дающих при делении на 4 в остатке 3.
В а р и а н т III
1. Найдите одиннадцатый член арифметической прогрессии – 4,2; –2; 0,2; …. Вычислите сумму первых одиннадцати ее членов.
2. Найдите десятый член геометрической прогрессии 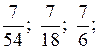 …
…
3. Сумма седьмого и четвертого членов арифметической прогрессии равна 6. Пятый ее член на 12 больше второго. Найдите первый и третий члены этой прогрессии.
4. Найдите все значения х, при которых значения выражений 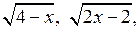 4 являются тремя последовательными членами геометрической прогрессии. 4 являются тремя последовательными членами геометрической прогрессии.
|
5. Найдите сумму всех трехзначных чисел от 100 до 450, которые при делении на 8 дают в остатке 5.
В а р и а н т IV
|
|
|
1. Найдите тринадцатый член арифметической прогрессии 5,2; 3,7; 2,2; …. Вычислите сумму первых тринадцати ее членов.
2. Найдите восьмой член геометрической прогрессии 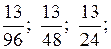 …
…
3. Пятый член арифметической прогрессии на 15 меньше второго. Сумма третьего и седьмого ее членов равна –6. Найдите третий и четвертый члены этой прогрессии.
4. Найдите все значения х, при которых значения выражений 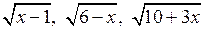 являются тремя последовательными членами геометрической прогрессии. являются тремя последовательными членами геометрической прогрессии.
|
5. Найдите сумму всех двузначных чисел, которые при делении на 5 дают в остатке 4.
Итоговая контрольная работа по алгебре
за курс основной школы
В а р и а н т I
Часть 1
1. Для каждого выражения из верхней строки укажите равное ему выражение из нижней строки: а) (а 2)3 а 2; б) (а 2 а 3)2; в) 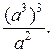
1) а 12; 2) а 10; 3) а 8; 4) а 7.
| О т в е т: | а | б | в |
2. Упростите выражение 4 у (у – 4) – (у – 8)2.
О т в е т: ____________________.
3. Сократите дробь 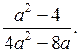
О т в е т: ____________________.
4. При каком значении х значение выражения 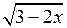 является числом рациональным?
является числом рациональным?
А. При х = 6. Б. При х = 0. В. При х = –3. Г. При х = –2.
| 5. В спортивном зале выделили помещение для раздевалки (на рисунке оно показано штриховкой). Какова площадь S оставшейся части зала? A. S = a 2 + аb + b 2. Б. S = a 2 + ab – b 2. B. S = a 2 – ab – b 2. Г. S = a 2 – ab + b 2. | 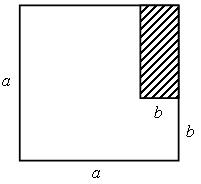
|
6. Укажите наибольшее из чисел:
–1,5; –0,5; (–0,5)3; (–1,5)3.
О т в е т: ____________________.
7. Какое из указанных чисел не делится на 3?
А. 12852. Б. 1143. В. 20293. Г. 7239.
8. В начале года число абонентов интернет-компании «Север» составляло 200 тыс. человек, в течение года 50 тыс. абонентов перешли в другие компании, а 60 тыс. новых абонентов присоединились к компании «Север». На сколько процентов увеличилось за год число абонентов этой компании?
А. На 5 %. Б. На 10 %. В. На 0,05 %. Г. На 105 %.
9. Решите уравнение 5 х 2 + 3 х – 2 = 0.
О т в е т: ____________________.
10. От одного города до другого автобус доехал за 3 ч, а автомобиль – за 2 ч. Скорость автомобиля на 25 км/ч больше скорости автобуса. Чему равно расстояние между городами?
Пусть расстояние между городами равно х км. Составьте уравнение по условию задачи.
О т в е т: ____________________.
| 11. На координатной плоскости отмечены точки С и D и через них проведена прямая. Какое уравнение задает прямую CD? A. х + у = 24. Б. х + у = 34. B. х – у = 4. Г. х – у = 5. | 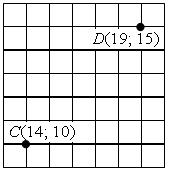
|
12. Решите неравенство 3 – х ³3 х + 5.
|
|
|
А. [–0,5; +∞). Б. (–∞; –0,5]. В. [–2; –∞). Г. (–∞; –2].
13. На координатной прямой отмечены числа а, b и с. Какая из разностей отрицательна?
| А. b – а. В. с – а. В. b – с. Г. с – b. | 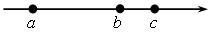
|
14. Последовательность задана формулой  Сколько членов этой последовательности больше 1?
Сколько членов этой последовательности больше 1?
А. 12. Б. 11. В. 10. Г. 9.
15. Функции заданы формулами:
1) у = х 2+ 1; 2) у = х 2 – 1;3) у = –х 2+1; 4) у = –х 2 – 1.
Графики каких из этих функций не пересекают ось х?
А. 1 и 4. Б. 2 и 4. В. 1 и 3. Г. 2 и 3.
16. Из пункта А в пункт В вышел пешеход, и через некоторое время вслед за ним выехал велосипедист. На рисунке изображены графики пути пешехода и велосипедиста. Определите, на сколько меньше времени затратил на путь из пункта А в пункт В велосипедист, чем пешеход.
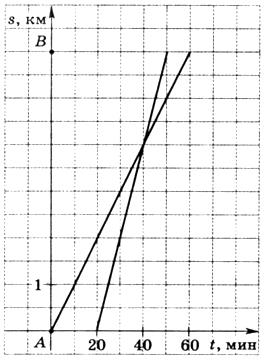
А. На 10 мин. Б. На 30 мин. В. На 50 мин. Г. На 20 мин.
Часть 2*
1. Решите систему уравнений 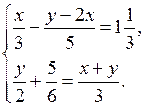
2. Лодка проплывает 15 км по течению реки и еще 6 км против течения за то же самое время, за которое плот проплывает по этой реке 5 км. Найдите скорость течения реки, если известно, что собственная скорость лодки равна 8 км/ч.
3. Парабола с вершиной в точке А (0; –3) проходит через точку В (6; 15). В каких точках эта парабола пересекает ось х?
4. При каких значениях параметра р система неравенств
 имеет решения?
имеет решения?
5. В арифметической прогрессии среднее арифметическое первых десяти ее членов равно 20. Найдите первый член и разность этой прогрессии, если известно, что они являются натуральными числами.
В а р и а н т II
Часть 1
1. Для каждого выражения из верхней строки укажите равное ему выражение из нижней строки: а) 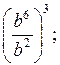 б) (b 4 b 3)2; в) b 4(b 3)2.
б) (b 4 b 3)2; в) b 4(b 3)2.
1) b 14; 2) b 12; 3) b 10; 4) b 9.
| О т в е т: | а | б | в |
2. Упростите выражение 6 а (а + 1) – (3 + а)2.
О т в е т: ____________________.
3. Сократите дробь 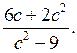
О т в е т: ____________________.
4. При каком значении х значение выражения  является числом иррациональным?
является числом иррациональным?
A. При х = 3. Б. При х = 0. В. При х = 1. Г. При х = –1.
| 5. В гараже выделили помещение для мойки машин (на рисунке оно показано штриховкой). Какова площадь S оставшейся части гаража? А. S = c 2+ ac – a. Б. S = c 2 – ac + a 2. В. S = c 2 + ac + a 2. Г. S = c 2 – ac – a 2. | 
|
6. Укажите наименьшее из чисел: –0,2; –1,2; (–0,2)3; (–1,2)3.
|
|
|
О т в е т: ____________________.
7. Какое из указанных чисел не делится на 9?
А. 81234. Б. 8883. В. 30159. Г. 3219.
8. В начале года в городской библиотеке было 50 тыс. книг. В течение года библиотечный фонд обновлялся. В связи с этим 10 тыс. книг списали и купили 16 тыс. новых. На сколько процентов увеличился за год библиотечный фонд?
А. На 6 %. Б. На 12 %. В. На 15 %. Г. На 40 %.
9. Решите уравнение 3 х 2 – 4 х – 4 = 0.
О т в е т: ____________________.
10. От турбазы до станции турист доехал на велосипеде за 3 ч. Пешком он смог бы пройти это расстояние за 7 ч. Известно, что идет он со скоростью, на 8 км/ч меньшей, чем едет на велосипеде. Чему равно расстояние от турбазы до станции?
Пусть расстояние от турбазы до станции равно х км. Составьте уравнение по условию задачи.
О т в е т: ____________________.
| 11. На координатной плоскости отмечены точки М и N и через них проведена прямая. Какое уравнение задает прямую MN? A. х + у = 20. Б. х + у = 26. B. х – у = 3. Г. х – у = 2. | 
|
12. Решите неравенство 2 + х £5 х – 8.
А. (–∞; 1,5]. Б. [1,5; +∞). В. (–∞; 2,5]. Г. [2,5; +∞).
13. На координатной прямой отмечены числа х, у и z. Какая из разностей положительна?
| А. х – у. В. z – у. Б. у – z. Г. х – z. | 
|
14. Последовательность задана формулой  Сколько членов этой последовательности меньше 1?
Сколько членов этой последовательности меньше 1?
А. 8. Б. 9. В. 10. Г. 11.
15. Функции заданы формулами:
1) у = х 2 + 2; 2) у = х 2 – 2; 3) у = –х 2 + 2; 4) у = – х 2 – 2.
Графики каких из этих функций пересекают ось х?
А. 1 и 4. Б. 2 и 3. В. 1 и 3. Г. 2 и 4.
16. Из пункта А в пункт В вышел пешеход, через некоторое время навстречу ему из пункта В в пункт А выехал велосипедист. Используя графики пути пешехода и велосипедиста, определите, на сколько больше времени затратил на весь путь пешеход, чем велосипедист.

А. На 10 мин. Б. На 30 мин. В. На 40 мин Г. На 60 мин.
Часть 2*
1. Решите систему уравнений 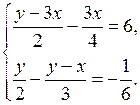
2. Катер проплывает 20 км против течения реки и еще 24 км по течению за то же самое время, за которое плот проплывает по этой реке 9 км. Скорость катера в стоячей воде равна 15 км/ч. Найдите скорость течения реки.
3. Парабола с вершиной в точке С (0; 5) проходит через точку В (4; –3). В каких точках эта парабола пересекает ось x?
4. При каких значениях параметра а система неравенств
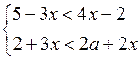 не имеет решений?
не имеет решений?
5. В арифметической прогрессии среднее арифметическое первых восьми ее членов равно 23. Найдите первый член и разность этой прогрессии, если известно, что они являются натуральными числами.
П р и м е ч а н и е:
*Задания этой части выполняются с записью решения.
|
|
|


