 |
Система линейных алгебраических уравнений
|
|
|
|
Решение Система линейных алгебраических уравнений всегда занимало математиков и для решения было разработано немало численных методов, подразделяющихся на прямые (Гаусса, Кремера) и итерационные (простых итераций, Зейделя,верхних релакций…)
EXCEL задача получения решение СЛАУ решаются с помощью вышеописанных матричных функций, для чего исходную систему надо представить в виде матричного уравнения.
Рассмотрим последовательность действий для получения решение СЛАУ на конкретном примере.
Задание 5
Найти решение системы линейных алгебраических уравнение и сделать проверку.




Для того, чтобы система (5) имела единственное решение необходимо и достаточно, чтобы определить системы, составленный из коэффициентов при переменных х,х,х,х, не был равен нулю.
Рассчитаем определить системы пользуясь функцией МОПРЕД. Рассчитанное значение определителя системы равно 1662723продолжать процесс поиска решения.
Из линейной алгебры известна матричная запись системы уравнений и матричное преставление решения.
Перепишем систему уравнений (5):
Тогда матричное решение уравнения выглядит так:
Результат, указанный на рис18 можно получить, выполнив следующие действия:
1. Вычислить определитель и выяснить имеет ли система единственное решение.
2. Вычислить матрицу обратную к исходной.
3. Найти произведение обратной матрицы и вектор столбца свободных членов.
Глава3. Поиск решения…
Оптимизация
Почти любую ситуацию, встречающуюся в деловой личной общественной жизни можно охарактеризовать как ситуацию принятия решения. Для задач принятия решений существенными являются следующие общие элементы:
|
|
|
1. Множества переменных и параметров. В их число входят:
Множество разрешающих или эндогенных переменных, значения которых рассчитываются лицом, принимающим решение.
Множество внешних или экзогенных переменных, значения которых не контролируются лицом, принимающим решение.
Множество параметров, которые так же контролируется и считаются в условиях задачи вполне определенными.
Модель- множество соотношений, связывающих все переменные и параметры.
Целевая функция- функция, функций, значение которой зависит от значений эндогенных переменных. Эта функция. Позволяет лицу, принимающему решения оценивать варианты.
Численные методы- методы, с помощью, которых можно систематически оценивать результаты различных решений.
Получение решения на модели, в конечном итоге, сводится к математической задаче нахождения некоторых вещественных значений эндогенных переменных, которые оптимизируют целевую функцию.
Если до недавнего времени все четыре перечисленные выше элемента ложились на лицо принимающее решение, то теперь умение пользоваться встроенными функциями EXCEL снимает наиболее утомительный пункт, а именно, применения численных методов, и делает исследование задач принятия решения более эффективными, так как теперь для решения одной и той же более эффективными, так как теперь для решения одной и той же задачи можно быстро просмотреть различного вида постановки в том числе и отличающиеся друг от друга по структуре.
Безусловный экстремум
Excel обладает мощным встроенным средством для нахождения экстремальных значений функции одной или нескольких переменных. Для одно-экстремальных функций можно найти безусловный глобальный экстремум. Для многоэкстремальных функций можно найти условный локальный экстремум. Забегая вперед отметим, что для многоэкстремальных функций определить какой из локальных экстремумов будет найден невозможно без построения графика функции на интересующем нас интервале, так как численные методы нахождения экстремума ориентированы на поиск ближайшего решения к точке начального приближения и вообще говоря, требуют унимодальности функции.
|
|
|
Посмотрим различные примеры поиска экстремальных значений функции.
Задание6
Найти минимум и максимум функции на интервале, построить график.
2. 
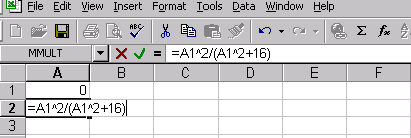
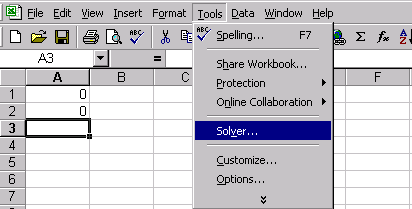

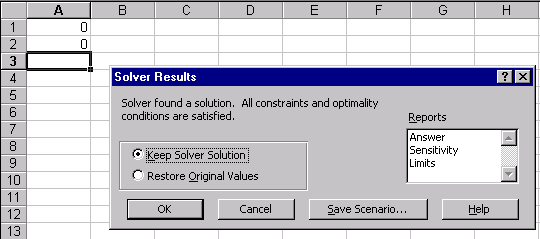



Рис.19
Для поиска безусловного экстремума функции сформируем лист электронной таблицы, как показано на рисунке 20. Функцию (6) запишем в клетку А2 где вместо переменной х следует указать адрес ячейки А1, которая содержит начальное приближение экстремума равное, например 0.
Для поиска минимума следует выполнить следующую последовательность действий:
1.Выполнить команду Сервис/Поиск решения…( получим лист электронной таблицы, как показано на рис.20).
2.Заполнить диалоговое окно Поиск решения… рис21
2.1.Щелкнуть левой клавишей мыши в поле. У становить целевую ячейку и щелкнуть на ячейке с формулой, в нашем случае это ячейка А2, абсолютный адрес которой. $А$2 появится в поле.
2.2. Выбрать поле Минимальное значение.
2.3. В поле. И зменяя ячейки ввести адреса ячеек, значения которых будут варьироваться в процессе поиска решения. В нашем случае это клеикаА1, абсолютный адрес которой. $А$1.
После выполнения пунктов 1-2 лист электронной таблицы будет выглядеть так, как показано на рис 21.
После щелчка на кнопке Выполнить получим решение поставленной задачи. В клетке А1 находится значение переменной Х равное 0.769231 при котором функция (5) достигает минимального значения равного –167,692. Рис22
Условный экстремум
Для функции одной переменной поиск экстремума возможен как на всей числовой оси, так и на некотором интервале, поиск на интервале уже можно считать поиском условного экстремума функции, т.к появляются ограничения на изменение значений аргумента.
На рис.21 в диалогом окне Поиск решения есть поле Ограничения м соответствующие ему команды: Добавить, Заменить, Удалить.
Рассмотрим предыдущую задачу, добавив условие поиска минимального значения на интервале [1;5]. Тогда диалоговое окно Поиск решения… следует видоизменить, добавив ограничения:
|
|
|
Щелкнув левой клавишей мыши в поле Ограничения и затем на кнопке Добавить, откроем диалоговое окно Добавление ограничения. Рис23,,,.. которое следует заполнить так как показано на рисунке.
После добавления последнего ограничения диалоговое окно Поиск решения… будет содержать математическую постановку задачи экстремума и выглядит след.образом.
После щелчка на кнопке Выполнить получим следующее решение:
У=-167 при х=1, отличающееся от решения, полученного в предыдущем случае. Здесь в качестве минимального значения выступает наименьшее значение функции на интервале[1;5], совпадающее с левой границей интервала.
Все численные методы нахождения оптимальных значений для корректной работы требуют,чтобы функция на интервале была унимодальной.
При такой постановке задачи значения труда и капитала определяется как 5 и 2 единицы соответственно. Получающиеся значение целевой функции при этом равно 3.37. Теперь можно построить график, на котором отражены линия безразличия использования труда и капитала при выпуске 3.37 и линия ограничения на средства, предназначенные для расходов на труд и капитал.
Полученные кривые касаются в найденной точке, что согласуется с теорией фирмы. Рис 31
 |
|
|
|


