 |
Математическое программирование
|
|
|
|
Различные методы оптимального управления, получившие заметное развитие во второй половине двадцатого века, благодаря созданию и распространению компьютерной техники, не только отвечают насущным потребностям экономической науки, но и начинают играть роль важнейшего ее составного элемента. И это вполне естественно, поскольку одной из главных задач экономической науки является разработка теоретического фундамента управления, т.е. методов наилучшего распределения ограниченных ресурсов (людских, материально -вещественных, финансовых, временных) для поддержания функционирования и развития предприятия или экономики страны.
Однако, чтобы обнаружить глубинную связь между математическим программированием и экономической наукой, понадобились усилия многих ученых.
Анализируя возможности Поиска решения … можно заметить, что он применим для решения достаточно широкого класса задач математического программирования.
Если задачу принятия решений в области управления можно сформулировать в виде подчиненных m произвольным ограничениям.
при
……………………
gm(x1,x2,…,xn) 
0
то Поиск решения… позволяет найти решение такой задачи, которая в формальной постановке может быть задачей:
1. линейного программирования
2. нелинейного программирования
3. целочисленного программирования
4. частично целочисленного программирования
Кроме того у лиц, принимающего решения есть возможность изменить параметры работы Поиска решения…, повышающие эффективность поиска оптимального решения. Рис.32
Линейное программирование
Найти минимум функции F =5 x 1 + x 2 
min
при ограничениях:
3 x 1 +4 x 2 12
|
|
|
-2 x 1 + x 2 
x 1 -2 x 2 
x 1 + x 2 
x 1, x 2 – произвольные
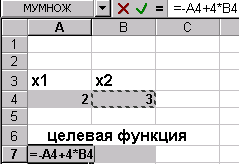
Сформируем страницу электронной таблицы и постановку задачи линейного программирования в диалоговом окне Поиска решения…
После выполнения поставленной задачи получаем следующее значение переменных
Как видим, при найденных значениях x 1, x 2 целевая функция принимает минимальное значение, равное –9.66 и этим удовлетворяются все ограничения поставленной задачи.
Графическое решение поставленной задачи выглядит так:
Задание 7
Решить задачу линейного программирования с помощью Поиска решения…, показать графически область допустимых решений и целевую функцию.
2.F=-x1+4x2 
при
3 x 1 +2 x 2 
2 x 1 - x 2 
-3 x 1 +2 x 2 
x 1 +2 x 2
x1 
Задание 8
По описанию задачи сделать математическую постановку, решить.создать отчет и прокомментировать его.
№2
Фирма изготовляет два типа электрических выключателей, типа А, доход от которых равен 0.4$. На каждый выключатель и типа В – доход от которых равен 0.3$. На изготовление выключателя А требуется в три раза больше рабочего времени, чем на изготовления типа В.
Если бы изготавливались выключатели только типа В, то дневного рабочего времени хватило бы для изготовления ровно 1000 выключателей. Поставка медного провода обеспечивает изготовление только 800 выключателей в день (любого типа). Для выключателей требуются специальные изоляторы, их можно получить в день для типа А не более 400, для типа В не более 700. Задача состоит в максимизации дохода при всех указанных выше ограничениях.
Задание 9
Составить задачу двойственную к данной задаче линейного программирования и решить обе с помощью Поиска решения…
2.F=-x1+x2 
при
x 1 +2 x 2 – x 3 £ 5
2 x 2 + x 4 £ 3
x 3 +2 x 4 £ 6
xj ³ 0.j=1.4
Задание 12
С помощью Поиска решения… найти решение системы нелинейных алгебраических уравнений. Исследовать зависимость получаемого решения от различных начальных приближений(менее трёх), оформить исследования в виде таблицы.
|
|
|
№2
ЛИТЕРАТУРА:
1. EXCEL 5.0 Для профессионалов. М-1995
2. EXCEL7.0 М-1997
3. А.А.Горчаков, И.В.Орлов. Компьютерные экономико-математические модели. М-1995
4. И.Л.Акулич. Математическое программирование а в примерах и задачах. М-1986
5. М.Кубонива. Математическая экономика на персональном компьютере. М-1991.
|
|
|
