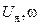 |
Импульсный способ управления двигателями ПТ
|
|
|
|
Этот способ управления основан на изменении интервала времени питания двигателя от источника постоянного напряжения в зависимости от требуемой скорости. Наибольшее распространение на практике получил широтно-импульсный способ управления, предусматривающий изменение длительности импульсов напряжения на якоре U япри постоянной частоте их следования. Если период T следования импульсов мал по сравнению с электромеханической постоянной времени tэм двигателя, то, несмотря на участки разгона t 1и участки торможения t 2 = T - t 1, частота вращения ω двигателя не успевает существенно измениться за время T. Она колеблется около своего среднего значения ωср, зависящего при постоянном моменте нагрузки от скважности импульсов 
или от коэффициента заполнения γ 
(рис. 1).
Изменение последнего в пределах 0 ≤ γ ≤ 1 в зависимости от величины управляющего сигнала позволяет получить соответствующие изменения скорости двигателя от нуля до максимального значения.
В зависимости от частоты следования импульсов ток якоря двигателя может иметь как прерывистый, так и непрерывный характер. Момент двигателя пропорционален среднему току якоря, следовательно, механические характеристики двигателя при импульсном управлении существенно зависят от характера изменения тока якоря. Для установления этой зависимости рассмотрим случай, когда якорь двигателя подключается с постоянной частотой коммутации к источнику питания через идеальный ключ.
(1)
(2)
|
|
где
– ток якоря; 
– активное сопротивление якоря; 
– индуктивность обмотки якоря; 
– противоЭДС, пропорциональная скорости вращения двигателя; E к– напряжение источника питания.|
|
|
|
|
Рис. 1. Импульсный способ управления
а – γ > 0,5; б – γ < 0,5
Уравнения (1) и (2) в общем случае имеют решения (рис. 2):
, (3)
, (4)
где 
и 
– начальные значения токов.
Рис. 2.Решение уравнений (1),(2)
Для случая прерывистых токов якоря 
, 
, где 
– значение тока якоря, достигаемое к концу первого интервала работы схемы в момент времени t' 1, т.е.
.
Во втором интервале коммутации ток якоря прерывается в момент времени t' 2(ключ разомкнут), поэтому, полагая 
, имеем
или
.
Среднее за период значение тока якоря определяется выражением
,
из которого после преобразования и подстановок получим:
.
Положив t '2<< T, 
.
Введя обозначения 
, 
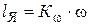, где 
– коэффициент противоЭДС, 
– коэффициент момента, окончательно получим:
.
Механические характеристики, описываемые полученным выражением, аналогичны характеристикам для случая регулирования скорости двигателя добавлением сопротивления R в цепь якоря двигателя.
Жесткость характеристики 
уменьшается по мере уменьшения g, делает режим прерывистых токов непригодным для использования в автоматических системах.
В режиме непрерывных токов во втором интервале коммутации ток якоря не уменьшается до нуля, а достигает значения 
. Поэтому, решая уравнения (3), (4) (рис. 3) и учитывая, что 
и 
, после несложных преобразований получим:
. (5)
Рис. 3. Решение уравнений (3),(4) 
Семейство механических характеристик двигателя описывается уравнением 
(рис. 4), которое аналогично случаю регулирования скорости двигателя при изменении напряжения генератора.
 |
Рис. 4. Семейство механических характеристик
В режиме непрерывных токов жесткость механических характеристик равна жесткости естественной характеристики двигателя. Поэтому непрерывность тока якоря является важнейшей качественной характеристикой импульсного регулирования.
|
|
|
От выбора частоты коммутации зависят энергетические показатели импульсного регулирования. При непрерывном токе якоря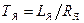 
, как следует из уравнения (5), t 1и t 2не влияют на величину среднего тока якоря. Однако от их соотношения зависят величина пульсации тока, а следовательно, дополнительные потери мощности по сравнению со случаем питания от генератора. Действительно,
(рис. 5),
где 
– пусковой ток якоря.
Максимальная амплитуда пульсаций тока якоря отвечает при неизменной частоте коммутации значению 
. На практике амплитуду пульсаций стремятся уменьшить, выбирая частоту коммутации из условия 
.
Рис. 5. Зависимость величины пульсаций тока
от коэффициента заполнения
Это позволит использовать приближенное выражение для 
и 
:
,
.
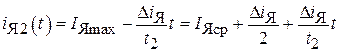Откуда после подстановки и преобразования получим 
.
|
|
|
