 |
Производные обратных тригонометрических функций.
|
|
|
|
Основы дифференциального исчисления. Понятие производной.
DX=X1-X – приращение аргумента.
Df(X)=f(X+DX)-f(X) – приращение функции. Пример:
Определение: Произв. функ. f(x) в точке Х наз. предел отношения приращения функ. к приращению аргум., когда последнее стремится к 0.
Геометрический смысл производной. 
Ку.к. – угловой коэф. касательной.
Ксек – угловой коэф. секущей. 
Таким образом угловой коэффициент касательной совпадает со значение производной в данной точке.
Уравнение касательной к графику функции y=f(x) в точке М0 (x0,y0) имеет вид: 
Физический смысл производной.
S(t) – путь за данное время.
DS(t) – приращение пути.
DS(t)/ Dt –средняя скорость на участке.
мгновен. скорость на участке: 
произв. пути от скорости: S'(t)=U(t)
Теорема: Связь между непрерывной и дифференцируемой функцией.
Функция наз. диферинцируемой если она имеет производную.
Если функция диффер. в точке х, то она и непрерывна в этой точке.
Доказательство: 
Правила дифференцирования
Теорема: Если f(x) и g(x) дифферен. в точке х, то: 
Доказательство 2-го правила. 
Теорема о произв. сложной функции.
Если y(x)=f(u(x)) и существует f’(u) и u’(x), то существует y’(x)=f(u(x))u’(x).
Доказательство:
Рассмотрим f(x) в задан. промеж.: [a,b].
g(y): [f(a),f(b)] – наз. обратной к f(x), если g(f(x))=x, для любого " X Î[a,b]
f(g(y))=y, для любого у Î[f(a),f(b)]
y=sin x [-p/2, p/2], тогда
x=arcsin y, yÎ[1,1]
sin arcsin y = y;
arcsin * sin x=x
Теорема о произв. обратной функции.
Таблица производных:
Таблица производных:
Доказательство:
Дифференциал функции.
Определение: Если Х независимая переменная, то дифференциал функции f(x) наз. f’(x)Dx=u обозначают df(x).
Теорема об инвариантной форме первого дифференциала.
|
|
|
df(x)=f’(x)dx
Доказательство:
1).
2). 
Производная высших порядков.
Определение: Производная второго порядка называется производная производной данной функции:
Определение: Производная n-го порядка называется производной производной n-1-го порядка.
Пример:
Используя метод математической индукции несложно показать, что:
1). n-ая производная обладает свойством линейности, т.е.:
2). 
3). 
4). 
5). 
6). 
Дифференцирование функций заданных параметрически.
Пример 1:
возьмем t=1, тогда x=2, y=3; y’(2)=7/3
Пример 2:
Основные теоремы матим. анализа.
Теорема Ферма.
Если f(x) дифф. в точке x0 и принимает в хтой точке наибольш. или наименьш. значение для некоторой окресности точки x0, то f’(x)=0.
Доказательство:
пусть f(x0) – наибольшая.
Теорема Ролля.
Если функция f(x) непрерывна на заданном промеж/ [a,b] деффер. на интервале (a,b) f(a)=f(b) то существует т. с из интерв. (a,b), такая, что f’(c)=0.
Теорема Коши.
Если f(x), g(x) удовл. трем условиям:
1). f(x), g(x) непрерыв. на промеж [a,b]
2). f(x), g(x) деффер. на интервале (a,b)
3). g’(x)¹0 на интер. (a,b), то сущ. т. с
g(b)¹g(a) (неравны по теореме Ролля).
1). F(x) – непрерывна на [a,b]
2). F(x) – дефференцированна на (a,b)
3). F(a)=0; F(b)=0
по теореме Ролля сущ. сÎ(a,b); F’(с)=0
Теорема Лагранжа.
Если функция f(x) непрерывна на [a,b] и дефференцирована на (a,b), то сущест.
т. с(a,b), такая, что: f(b)-f(a)=f’(c)(b-a).
Доказательство: применим т.Коши, взяв только g(x)=x, тогда g’(x)=1¹0.
Правила Лопиталя.
Раскрытие неопределенности.
Теорема: Если функция f(x), g(x) дефференцирована в окресности т. а, причем f(a)=g(a)=0 и существует предел
Доказательство:
Формула Тейлора.
Определение: многочлен Тейлора n-го порядка функции f(x) в точке x0 назыв.
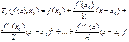
Пример: 
Определение: остаточным членам формулю Тейлора n-го порядка наз.:
Теорема: Если функция F(x) (n+1) – дефферен. в окресности точки x0, то для любого x из этой окресн. сущ. т. с(x0, x)
|
|
|
Правила дифференцирования.
Производные степенных и тригонометрических функций.
Основные формулы: 
Производная сложной функции.
Производные показательных и логарифмических функций.
Основные формулы:
Если z=z(x) – дифференцируемая функция от x, то формулы имеют вид:
Производные обратных тригонометрических функций.
Основные формулы: 
Для сложных функций:
|
|
|
