 |
Аналитические признаки поведения функции.
|
|
|
|
Теорема: Критерий постоянства фун.
Функция f(x)=const на промежутке [a,b], тогда, когда f’(x)=0 на интервале (a,b).
Док-во: f(x)=c => f’(x)=c’=0 возьмем "xÎ[a,b] и применим т. Лангранжа f(x) [a,b] по т. Лангранжа f(x)-f(a)=f’(c)(x-a); cÎ(a,x); f(x)-f(a)=0; f(x)=f(a) для любого x => f(x)=const.
Теорема: Достаточный признак возрастания функции. Если f’(x)>0, (a,b), то f(x) возрастает на [a,b].
Док-во:
возьмем x1, x2 Î[a,b]: x1<x2 => f(x2)>f(x1)
применим т. Лангранжа f(x) на [x1,x2]
по этой теореме f(x2)-f(x1)=f’(c)(x2-x1)>0 => f(x2)>f(x1). Замечание: данные условия не являются необходимыми.
Теорема: достаточный признак убывания функции. Если f’(x)<0 на (a,b), то f(x) убывает на [a,b].
Док-во 1: подобно предыдущему.
Док-во 2: g(x)=-f(x),тогда g’(x)=-f’(x)>0
=> g(x) - возрастает => f(x) – убывает.
Несложно показать, что если функция возрастает (убывает) на [a,b], то ее произв. не отрицат.(положит.) на (a,b).
f(x) возрастает: [a,b]=>f’(x)Ê0 (a,b).
Признаки экстремума функций.
Опред: точка x0 называется точкой max (min) если существ. такая окрестность данной точки, что в x0 фун. принимает наибольшее (наименьшее) значение.
Точка х0 наз. точкой экстремума, если эта точка max или min данной функции.
Теорема: Необходимый признак экстремума функции.
Если х0 точка экстремума f(x), то:
1). Либо не существует f’(x0)
2). Либо f’(x0)=0
Док-во:
1). Не сущест. f’(x0)
2). Сущест. f’(x0) - по т. Ферма f’(x0)=0
Замечание: данные условия не являются достаточными.
Поиск наибольшего и наименьшего значения непрерывных функций на замкнутом промежутке.
Теорема: Первый достаточный признак экстремума функции.
Если f’(x)>0 на интервале (x0-б,х0) и f’(x)<0 на интервале (х0,x0+б) т.е. меняет знак с плюса на минус при переходе на точку х0, т.е. х0 – точка максимума f(x), а если же меняет знак с минуса на плюс, то х0 – точка минимума.
|
|
|
Доказательство:
Теорема: Второй достаточный признак максимума функции.
Если f(x) имеет непрерывную вторую производную в окрестности точки х0, и:
1). f’(x0)=0 2). f’’(x0)<0
то х0 точка максимума (аналогично, если f’’(x0)<0, то х0 – точка минимума)
Док-во: Возьмем окрестность, где вторая производная сохраняет знак и запишем формулу Тейлора 1-го порядка для х из данной окрестности.
Выпуклость графика функции.
Опр. График функции y=f(x) называется выпуклым вниз (вверх) если он расположен выше (ниже) любой касательной проведенной к графику функции на данном интервале.
Теорема: Достаточный признак выпуклости графика функции вниз.
Если функция f(x) дважды дефференц. на нтервале (a,b) и ее вторая производн. f’’(x)>0 на интервале (a,b), то график функции y=f(x) выпуклый вниз на интервале (a,b).
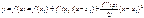Уравнение касательной:
Возьмем X=x.Из первого вычтем второе
Поэтому y>Y следовательно график функции расположен выше касательной
Аналогично, если f’’(x)<0 на (a,b) то график функции y=f(x) - выпуклый вверх, на данном интервале.
Асимптоты.
Опр. Часть графика называется бесконечной ветвью если при движении точки по этой части, расстояние между ей и началом координат стремится к бесконечности.
Опр. Прямая называется асимптотой бесконечной ветви графика функции, если при удалении точки от начала координат по этой ветви, расстояние до данной прямой стремится к нулю.
Теорема 1: x=a (вертикальная прямая) – является асимптотой для бесконечно вертикальной ветви графика функции y=f(x), тогда когда f(x)®µ, при x®a.
Теорема 2: Критерий существования наклонной асимптоты прямая y=kx+b является асимптотой для правой (левой) ветви графика функции тогда, когда существует предел при:
Док-во: Точка M0(x0,y0) и прямая
L: Ax+By+Cz=0, то расстояние
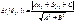
Пусть y=kx+b
асимптота =>
d(M,l)®0=>
|
|
|
kx-f(x)+b®0
тогда f(x)-kx®b
при x®+µ
существует предел:
Теорема: Необходимый признак существования наклонной асимптоты. Если прямая l: y=kx+b –
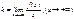наклонная асимп. для правой наклонной ветви, то:
Док-во:
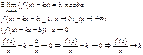Пример:
x=1 – верт. Асимптота, т.к.
f(x)®µ, когда x®1
Вывод: y=0×y+1 – наклонная асимптота для левой и правой ветви.
|
|
|
