Динамическое исследование машинного агрегата

В курсовом проекте рассматриваются машинные агрегаты двух типов: рабочие машины (см. рис. 3.5, а) и машины-двигатели (см. рис. 3.5, б).

При работе машины происходят колебания угловой скорости кривошипного вала ω, вызванные переменностью приведенного момента М_п (φ) сил и приведенного момента инерции звеньев кривошипно-ползунного и некоторых вспомогательных механизмов J_п (φ). Для учета влияния названных причин на закон движения вала кривошипа составляется упрощенная динамическая модель машинного агрегата в виде вращающегося звена приведения (рис. 3.6, а).

 

 

а)

			Передаточный механизм		Исполнительный механизм

 

 

ω

Мп

_д

		Вспомогательный механизм

 

б)

		Вспомогательный механизм

 

 

Р и с. 3.5. Схемы машинных агрегатов

 

 

а) б)

Jп рыч

Jп д

JпМ

Jкр

Jп с

 

w1 j1 Мпс

Мп с   Мп д

JпII=var

Jп I =const

 

Р и с. 3.6. Динамическая модель машинного агрегата

 

Звено приведения, в качестве которого обычно принимается кривошип, обладает приведенным моментом инерции J_п и находится под действием приведенного момента сил М_п, причем , М – приведенный момент движущих сил; М – приведенный момент сил сопротивления.

Приведенный момент инерции можно, в свою очередь, представить в виде суммы постоянной и переменной J_пII составляющих. В величину входят моменты инерции вращающих узлов агрегата: собственный момент инерции кривошипа J , приведенные моменты инерции ротора электродвигателя J_{п д}, момент инерции добавочной массы (маховика) J_пМ и передаточного механизма J_п.м. (рис. 3.6, б).Переменная составляющая J_пII обусловлена рычажным механизмом, каждое звено которого имеет собственный переменный момент инерции, зависящий от положения механизма.

Основными задачами динамического исследования машинного агрегата на стадии установившегося движения являются:

- определение момента инерции дополнительной массы (маховика) J_пМ, необходимой для обеспечения требуемой степени неравномерности вращения звена приведения в установившемся режиме, задаваемой коэффициентом неравномерности движения ;

- определение закономерности вращения () звена приведения для любых положении механизма внутри периода установившегося движения.

Для решения этих задач воспользуемся приближенным методом проф. П.И. Мерцалова (см. лекц. №4).

Переменная составляющая приведенного момента инерции , кг /м² находится из условия

J_пII =m₂[(x'_s2)²+(y' _s2)²]+J_s2 и²₂₁ +m₃ и²₃₁, (3.2)

где x'_s2, y'_s2, и₂₁, и ₃₁ – аналоги линейных и угловых скоростей (передаточные функции); J_s2 – момент инерции звена 2 (шатуна) относительно оси, проходящей через центр масс, кг/ м².

Производная приведенного момента инерции J_пII по обобщенной координате имеет вид

, (3.3)

где x"_s2, y"_s2, и '₂₁, и '₃₁ – аналоги линейных и угловых ускорений.

Приведенный момент сил М_п определяется из условия равенства мгновенных мощностей. Так, для рабочей машины, если в качестве звена приведения принимается вал кривошипа, приведенный момент сил сопротивления М_{п с}, равен:

- для механизмов с горизонтальным движением ползуна:

М_пс ; (3.4)

- для механизмов с вертикальным движением ползуна:

М_пс . (3.5)

Сила полезного сопротивления для каждого из рассматриваемых положений механизма находится путем обработки механической характеристики. Приведенныймомент движущих сил М_пд для рабочих машин (по методу Мерцалова) в дальнейшем предполагается постоянным по величине М_пд =соnst и находится из условия равенства работ движущих сил и сил сопротивления за цикл установившегося движения. Для машин-двигателей по формулам (3.4) и (3.5) определяется М_пд, a М_пс =соnst.

Ниже приводится алгоритм решения для рабочей машины. Для машин-двигателей в формулах (3.6)-(3.10) необходимо поменять индекс «с» на «д» и наоборот.

Работа сил сопротивления за цикл установившегося движения :

А _с= 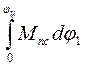, Дж. (3.6)

При М =const и с учетом того, что за цикл установившегося движения

, находим М_пд , (3.7)

причем, обычно радиан.

Далее для каждого рассматриваемого положения механизма i определяются следующие параметры:

- работа движущих сил, Дж:

A_дi=M_пд ; (3.8)

- приращение кинетической энергии машинного агрегата, Дж:

; (3.9)

- кинетическая энергия звеньев механизма с переменным приведенным моментом инерции, Дж:

Т , (3.10)

где – средняя угловая скорость кривошипа за цикл установившегося движения;

- изменение кинетической энергии звеньев машинного агрегата с постоянным приведенным моментом инерции, Дж:

. (3.11)

Далее определяются минимальное 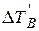и максимальное значение из массива , а затем максимальное изменение кинетической энергии звеньев с постоянным приведенным моментом инерции, Дж:

. (3.12)

Приведенный постоянный момент инерции звеньев машинного агрегата, необходимый для обеспечения требуемой неравномерности движения, кг м²:

. (3.13)

Дополнительное значение постоянной составляющей приведенного момента инерции, т.е. момент инерции маховика, в кг м², определяется из выражения

= J_{п 0} кг/м², (3.14)

где J_{п 0} – суммарный приведенный момент инерции всех вращающихся звеньев машинного агрегата (ротора двигателя, зубчатых колес передаточного механизма, вала кривошипа и т.д.).

В случае если J_п0 больше , маховик устанавливать нет необходимости.

Для определения истинного значения угловой скорости звена приведения вычисляются средние значения изменения кинетической энергии, Дж

, (3.15)

и среднее значение кинетической энергии звеньев с постоянным приведенным моментом инерции, Дж

. (3.16)

Для каждого положения механизма i вычисляется:

- кинетическая энергия, Дж:

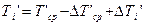; (3.17)

- w ₁ – угловая скорость звена приведения, с^-i:

 

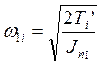; (3.18)

 

- угловое ускорение звена привидения, с^-2:

. (3.19)

 

⇐ Предыдущая1234567Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: