Используют тригонометрические формулы для суммы и разности двух углов и получают

Тема: Элементы высшей алгебры

Комплексные числа.

Решение алгебраических уравнений – важнейшая задача математики. Стремление сделать разрешимыми уравнения различных типов приводит к необходимости расширения понятия числа.

 

Вид уравнения Тип числа ____ Множество:

x + a = b отрицательные и 0

a x = b дробные

====== > Q - рациональных чисел

x ² = 2 иррациональные

=======> R - действительных чисел

x² + 1 = 0 комплексные

========= > C -комплексных чисел

Корень уравнения х² = - 1 наз. мнимой единицей и обозначается символом i (Эйлер). Символ i определяетсяусловием i ² = - 1.

Опр. Комплексным числом наз. выражение вида а + b i, где а, b R, i -мнимая единица.

Обозначения: a + b i = z, a = Re z -действительная часть КЧ, b i = Im z -мнимая часть КЧ, b -коэффициент мнимой части.

При а = 0 имеем чисто мнимое число, при b = 0 - действительное число. КЧ z = a + b i и z* = a – b i наз. сопряженными, а форма записи КЧ алгебраической.

Пр. Решим уравнение x² – 2x + 5 = 0.

x_1,2 = (2 ) /2 = 1 = 1 = 1 = 1 2 i

Таким образом, корнями квадратного уравнения с отрицательным дискриминантом являются сопряженные КЧ.

 

Равенство КЧ. a + b i = c + d i означает равенство коэффициентов: a = c, b = d

Сложение КЧ. (a + b i) + (c + d i) = (a + c) + (b + d) i -означает раздельное сложение вещественных и мнимых частей. (Это два определения.)

Пр. z₁ = 2 – 3i, z₂ = 1 + 4i, z₁ + z₂ = 3 + i, z + z* = 2 a

Умножение КЧ. (a + b i) (c + d i) = (a c - b d) + (a d + b c) i

Это обычное перемножение двучленов с учетом i ² = - 1.

Пр. z₁ z₂ = 14 + 5 i, z z* = (a + b i) (a - b i) = a² + b²

т. е. произведение сопряженных КЧ есть число действительное.

Деление КЧ. Частным от деления двух КЧ z₁ / z₂ является третье КЧ z₃, произведение которого на делитель дает делимое z₃ z₂ = z₁

Для того чтобы разделить два КЧ необходимо числитель и знаменатель дроби умножить на КЧ сопряженное знаменателю

 

a + b i = (a + b i) (c – d i) = (a c + b d) + (b c – a d) i

c + d i (c + d i) (c – d i) c² + d²

Пр. z₁ / z₂ = - 10/17 - 11/17 i

Степени i. i¹ = i i^{4 n + 1} = i

i² = - 1 i^{4 n + 2} = - 1 Пр. i²⁴ = 1, i⁵⁹ = i ^{56+ 3} = - i

i³ = - i i^{4 n + 3} = - i

i⁴ = 1 i^{4 n} = 1

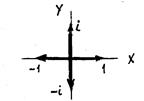
Геометрическая интерпретация КЧ.

Действительному числу соответствует точка на числовой оси, а КЧ a + b i соответствует точка M (a;b) на координатной плоскости или её радиус-вектор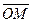

Такая плоскость наз. комплексной плоскостью, ось Ох – действительной осью, ось Оу - мнимой осью. Модулем КЧ наз. модуль радиус-вектора .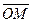

| z | = r = =

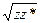
Аргументом КЧ z = a + i b (Arg z) наз. угол между Ох и 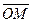. Он определяется неоднозначно, с точностью до 2 . Главное значение аргумента: arg z = , - < < .

Arg z = arg z + 2 k , k = 1,2,3,...

Алгоритм вычисления аргумента:

1) найти острый угол = arctg | b/ a |; 2) определить квадрант, в котором находится ОМ; 3) перейти от к по правилу: в 1 четверти = ; во 2 четверти = - ; в 3 четверти = + ; в 4 четверти = 2 -

Пр. Найти аргумент z = 1 – i .

= arctg |- / 1 | = arctg = / 3. Вектор OM лежит в 4 четверти, следовательно, Arg z = (2 - ) + 2 k = 5 /3 + 2 k , k N

Сложение двух КЧ геометрически означает сложение двух радиус-векторов.

 

Тригонометрическая форма КЧ.

Коэффициенты КЧ (a + b i) можно выразить через его модуль и аргумент:

{ cos = a/ r, sin = b/ r } { a = r cos , b = r sin }

и записать КЧ в форме

z = r [ cos ( + 2 k ) + sin ( + 2 k ) ]

которая наз. тригонометрической формой КЧ

 

Пр. Записать число z = - - i в тригонометрической форме.

Находим модуль r = [ (- )² + (-1)² ] ^{1/ 2} = 2. Определяем = arctg 1/ = /6. Вектор ОМ в 3 четверти arg z = + / 6 = 7 / 6, z = - - i = 2(cos7 / 6 + i sin 7 / 6).

Пр. Записать число z = 2 (cos 330⁰ + i sin 330⁰ ) в алгебраической форме.

cos 330⁰ = cos (360⁰ – 30⁰) = cos 30⁰ = /2, sin 330⁰ = sin (360⁰ – 30⁰) = - sin 30⁰ = -1/2,

тогда a = 2 ( / 2) = , b = 2 (-1/2) = -1 и z = - i.

При перемножении и делении двух КЧ в тригонометрической форме

z₁ = r₁ (cos ₁ + i sin ₁), z₂ = r₂ (cos ₂ + i sin ₂)

используют тригонометрические формулы для суммы и разности двух углов и получают

z₁ z₂ = r₁ r₂ (cos ( ₁ + ₂ ) + i sin ( ₁ + ₂ ))

z₁ / z₂ = r₁/ r₂ (cos ( ₁ - ₂ ) + i sin ( ₁ - ₂ ))

z ⁿ = [r (cos + i sin )] ⁿ = r ⁿ (cos n + i sin n )

= [ cos ( + 2 k)/ n + i sin ( + 2 k)/ n) ], где k = 0,1,2,..., n – 1.

Умножение КЧ теперь сводится к умножению их модулей и сложению аргументов, а деление КЧ к делению модулей и вычитанию аргументов. Появление n решений при извлечении корня связано с тем, что все значения Arg z = ( + 2 k ) уменьшаются в n раз и самые первые n значений аргумента становятся меньше 360⁰, т.е. становятся главными значениями аргумента - arg z. Они различны, но при возведении корней в степень n получаемодинаковый результат.

Пр. Пусть arg z = 40⁰, тогда Arg z = arg z + 2k , где k = 0,1,2,... или

z 40⁰, 400⁰, 760⁰, 1120⁰,… Имеем 1 главное значение аргумента.

z² 80⁰, 800⁰, 1520⁰, 2240⁰, … Имеем 1 главное значение аргумента.

z^1/2 20⁰, 200⁰, 380⁰, 560⁰, … Имеем 2 главных значения аргумента.

z^1/4 10⁰, 100⁰, 190⁰, 280⁰, … Имеем 4 главных значения аргумента.

Показательная форма КЧ.

Существует формула Эйлера exp (i ) = cos + i sin , которая приводит к показательной форме КЧ

z = a + i b = r (cos + i sin ) = r exp (i )

(I) (II) (III)

В алгебраической форме (I) КЧ удобно складывать и вычитать, а в тригонометрической форме (II) и в показательной (Ш) умножать, делить.

 

r₁ exp (i ₁) r₂ exp (i ₂) = r₁ r₂ exp i ( ₁ + ₂

r₁ exp (i ₁) / r₂ exp (i ₂) = r_1/ r₂ exp i ( ₁ - ₂

(r exp i )ⁿ = rⁿ exp i n

(r exp i )^1/n = r^1/n exp i ( +2 k )/ n, k = 0,1,2,3,..., n - 1.

Рассмотрим извлечение корней из действительных чисел. Пусть z = a и a > 0, т.е. перед числом а стоит множитель 1 = (cos 0 + i sin 0) или – 1 = (cos + i sin ). Тогда, при z > 0 z^{1/ n} = а ^{1/ n} (cos + i sin ), где k = 0,1,2,..., n – 1, а при z < 0 z^{1/ n} = а ^{1/ n} (cos + i sin ).

Пр. = (cos 0 + i sin 0)^1/4 = cos 2 k/ 4 + i sin 2 k /4, где k = 0,1,2, 3. Получаем корни: z ₀ = (cos 0 + i sin 0) = 1, z ₁ = (cos /2 + i sin /2) = i, z ₂ = (cos + i sin ) = - 1, z ₃ = (cos 3 /2 + i sin3 /2) = - i. Проверка: (1)⁴ = (i)⁴ = (-1)⁴ = (- i)⁴ =1

Пр. Вычислить (- 81)^1/.4 . Решение (- 81)^{1/ 4} = (- 1 81)^1/4 = (cos + i sin )^{1/ 4}

= 3 (cos ( + 2 k )/ 4 + i sin ( + 2 k )/ 4), k = 0, 1, 2, 3.

z₀ = 3(cos / 4 + i sin /4) = 3 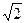/2(1 + i)

z₁ = 3 (cos ( /4 + /2) + i sin( /4 + /2)) = 3 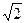/2(1 - i)

z₂ = 3 (cos ( /4 + ) + i sin( /4 + )) = 3 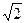/2(-1 - i)

z₃ = 3 (cos ( /4 + 3 /2) + i sin( /4 + 3 /2)) = 3 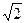/2(1 - i)

Решения изображают 4 вектора с r = 3 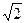/2 и ₀= /4, ₁ =3 /4, ₂ =5 /4 ₃ =7 /4

 

Таблица 1. 0⁰ 30⁰ 45⁰ 60⁰ 90⁰

sin 0 1/2 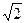/2 /2 1

cos 1 /2 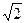/2 ½ 0

Таблица 2

90⁰- 90⁰+ 180⁰- 180⁰+ 270⁰ - 270⁰ + 360⁰ - .

sin sin cos cos sin - sin - cos - cos - sin

cos cos sin - sin - cos - cos - sin sin cos

Пр. Даны z₁ = 12 (cos 225⁰ + i sin 225⁰), z₂ = 3/2 (cos 75⁰ + i sin 75⁰). Найти z₁ z₂, z₁ /z₂

z₁ z₂ = 18 (cos (225⁰+ 75⁰) + i sin (225⁰ + 75⁰)) = 18 (cos(360⁰ – 60⁰) + i sin(360⁰ – 60⁰)) =

= 18 (cos 60⁰ - i sin 60⁰) = 18 (½ - i /2) = 9 - 9 i

z₁/ z₂ = 8 (cos (225⁰– 75⁰) + i sin(225⁰ – 75⁰)) = 18 (cos (180⁰ – 30⁰) + i sin (180⁰– 30⁰)) =

= 8 (- cos 30⁰ + i sin 30⁰) = 8 (- /2 + i ½) = - 4 + 4 i

Опорные конспекты лекций.

12Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: