 |
Задачи предварительного эксперимента. Факторное пространство
|
|
|
|
Содержание
Введение
Элементы математической статистики
Оценки параметров распределения
Наиболее важные распределения, применяемые в математической статистике
Нормальное распределение
1.2.2 Распределение Пирсона (х2 распределение)
Распределение Стьюдента
Распределение Фишера
2. Организация эксперимента
Задачи предварительного эксперимента. Факторное пространство
Формулирование цели эксперимента и выбор откликов
Выбор и кодирование факторов
Список литературы
Приложение (таблица критических точек критерия Фишера)
Введение
К важнейшим направлениям научно-технического прогресса относятся автоматизация производства, широкое применение компьютеров и роботов, создание гибких автоматизированных устройств и т.д. Во всех этих направлениях ведущая роль принадлежит электронике.
При создании электронной и электромеханической аппаратуры основные трудозатраты приходятся на ее настройку, снятие характеристик и испытания. При этом нередко используется малоэффективный традиционный метод однофакторного эксперимента, недостаточно внимания уделяется организации и планированию эксперимента и вероятностно-статистическому анализу получаемых данных. Чтобы повысить производительность труда в данной области, специалистам необходимо знать основы математической теории эксперимента и успешно применить ее на практике.
Элементы математической статистики
Оценки параметров распределения
Математическая статистика изучает массовые, случайные явления. Ее основной задачей является изучение распределений случайных величин или ее числовых характеристик (параметров распределения) на основе экспериментальных данных. Среди параметров распределения наиболее часто используются математическое ожидание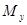 
, дисперсия 
и среднее квадратическое отклонение 
. По результатам эксперимента можно вычислить точечные и интервальные оценки этих параметров.
|
|
|
Точечные оценки определяют приближенные значения неизвестных параметров.
Пусть в результате экспериментов были получены следующие значения выходной переменной 
.
Оценкой математического ожидания является выборочная средняя:
Оценка дисперсии определяется формулой:
Для среднего квадратического отклонения получим:
Если среди результатов попадаются одинаковые значения, то есть значения 
встретилось 
раз, то точечные оценки определяются формулами:
,
где 
-число различных значений 
.
Интервальные оценки указывают интервал, в который с заданной вероятностью попадает значение неизвестного параметра.
Для математического ожидания доверительный интервал оценивается следующим образом:
,
где 
-значение критерия Стьюдента.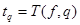 
, 
-число степеней свободы, 
-уровень значимости.
Среднее квадратическое отклонение имеет доверительный интервал:
,
где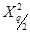 
- значение критерия Пирсона для уровня значимости 
, 
- для уровня значимости 
, -число степеней свободы.
Наиболее важные распределения, применяемые в математической статистике
Нормальное распределение
Случайная величина 
, распределенная по нормальному закону, описывается плотностью вероятности:
.
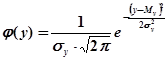Нормальное распределение определяется двумя параметрами – математическим ожиданием 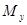и среднеквадратическим отклонением .
Случайная величина 
имеет математическое ожидание 
и среднеквадратичное отклонение 
и называется нормированной нормально распределенной случайной величиной. Ее плотность вероятности:
|
|
|
,
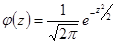График плотности распределения приведен на рисунке 1.
Функция распределения 
табулирована.
Вероятность попадания в интервал 
:
Вероятность попадания в интервал [-3;3] длиной 
по правилу “3-х сигм” принимается за единицу. Это равносильно предположению, что все значения z заключены в интервал [-3;3].
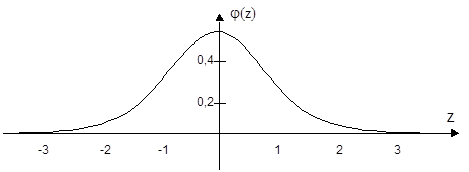
Рис.1. График функции плотности нормированной нормально распределенной случайной величины
1.2.2 Распределение Пирсона (х2 распределение)
Это распределение используется для построения доверительных интервалов, проверки соответствия эмпирического распределения некоторой теоретической зависимости, проверки согласованности мнений экспертов.
Пусть имеется 
независимых, нормированных, нормально распределенных случайных величин 
. Сумма их квадратов образует новую случайную величину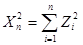 
.
Число степеней свободы равно числу независимых слагаемых в сумме. Если на слагаемые наложено 
связей, то число степеней свободы будет равно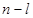 
.
Распределение 
является асимптотически нормальным и зависит только от числа степеней свободы 
. Значение табулированы.
Распределение Стьюдента
Для построения доверительных интервалов и для проверки статистических гипотез часто используется 
-распределение (распределение Стьюдента).
- оценка математического ожидания,
- оценка СКО, рассчитанные по результатам 
опытов, случайной величины , распределенной по нормальному закону с параметрами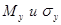 
.
Распределение Стьюдента определяется числом степеней свободы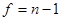 
, является симметричным, унимодальным и асимптотически нормальным. При 
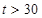оно практически совпадает с нормальным. Таблица распределения имеет два входа – число степеней свободы и уровень значимости 
. На пересечении находится значение 
, которое удовлетворяет условию 
.
Распределение Фишера
Это распределение, как и два предыдущие, используются при анализе результатов эксперимента, имеющих нормальное распределение. 
- распределение задается следующим образом:
,
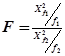где 
- случайные величины с числом степеней свободы 
, причем величина в числителе должна быть больше величины в знаменателе.
|
|
|
Путем тождественных преобразований приведем, 
к отношению двух оценок дисперсии некоторой случайной величины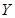 
.
Пусть на основе результатов двух серий экспериментов с числом опытов 
соответственно были получены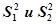 
-оценки дисперсии 
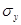с числом степеней свободы 
. Заметим что,
,
тогда можно записать:
.
Отсюда 
. Предполагается, что 
.
-распределение определяется двумя параметрами – числами степеней свободы большей дисперсии 
и меньшей дисперсии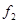 
. Критические значения -распределения, соответствующие уровню значимости 
даны в приложении. Таблица содержит значения 
, удовлетворяющие условию 
Организация эксперимента
Задачи предварительного эксперимента. Факторное пространство
Непосредственному проведению основного эксперимента предшествует подготовительная работа – предпланирование, которое состоит из следующих этапов:
1. Изучение объекта и формулировка цели экспериментального исследования;
2. выбор откликов (выходных переменных);
3. выбор факторов (входных переменных) и их интервалов варьирования;
4. разработка экспериментальной установки и метрологического обеспечения или программ для ЭВМ;
5. составление таблицы условий и плана эксперимента.
Примером многооткликового объекта является импульсное устройство, в котором откликами могут быть ширина и амплитуда импульса, временное запаздывание. Эти параметры – отклики зависят от внутренних параметров устройства и различных внешних воздействий: напряжения питания, температуры окружающей среды, внешних электромагнитных полей.
На рис.2 показана схема многофакторного эксперимента, которую иногда называют схемой черного ящика. Выходные переменные, определяющие состояние объекта (переменные состояния), обозначены буквами 
. Они зависят от трех типов воздействий обозначаемых векторами 
.
Первая группа 
- это контролируемые и управляемые в процессе эксперимента, независимые между собой переменные, которые называют факторами.
|
|
|
Вторая группа воздействий 
- наблюдаемые, но неуправляемые переменные.
Третья группа воздействий 
- ненаблюдаемые и неуправляемые переменные.
Задача эксперимента состоит в том, чтобы получить зависимость вектора отклика 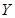от воздействия факторов 
:
.
Воздействия 
являются шумом или возмущениями, которые могут искажать искомую зависимость. Чтобы ослабить действие возмущений на 
используют обычные методы стабилизации условий эксперимента и защиты объекта от помех.
Рис 2. Объект исследования многофакторного эксперимента
Пространство, образованное координатами 
, называется факторным. Каждому набору значений факторов 
соответствует точка 
в факторном пространстве и некоторое значение отклика 
.
|
|
|
12 |
