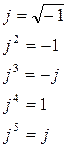|
Метод наложения (суперпозиции)
|
|
|
|
Исходные данные:
E 1=40 В r 1=0,4 Ом
E 2=30 В r 2=0,4 Ом
R 1=30 Ом
R 2= R 3=10 Ом
R 4= R 5=3,6 Ом
Заменяем сложную цепь двумя простыми, т.к. в схеме два источника.
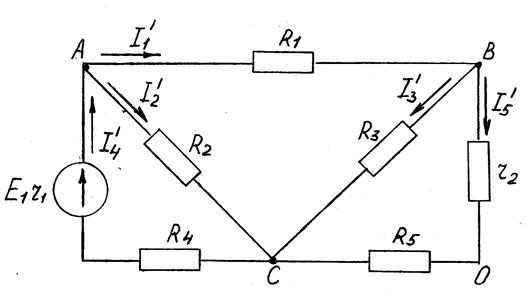
Рисунок 8
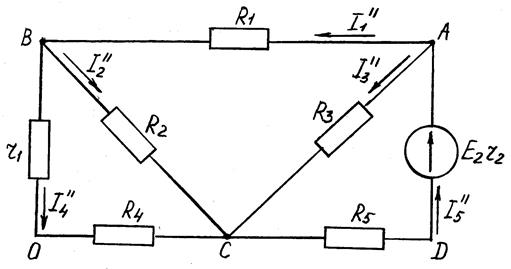
Рисунок 9
Методом свертывания рассчитываем простые цепи и находим частичные токи.
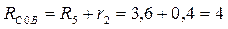 Ом
Ом

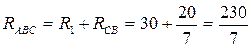
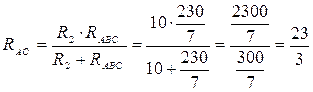
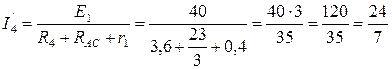
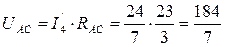

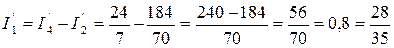
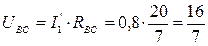
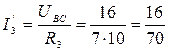
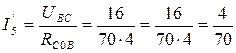
Сопротивления рассчитываются точно так же
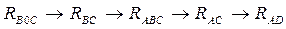

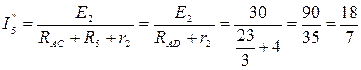


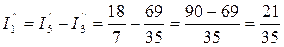

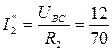
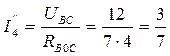
Находим реальные токи в ветвях
 А
А
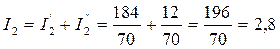 А
А
 A
A
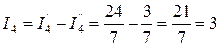 А
А
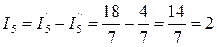 А
А
Проверка: Баланс мощностей
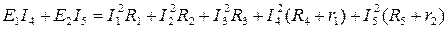
180=180
Это означает, что задача решена верно.
Задача 2
Для электрической цепи переменного тока, изображённой на рисунке 10, в таблице 2 заданы значения сопротивлений всех элементов, а также один дополнительный элемент. Начертить схему цепи и определить следующие величины, если они не заданы в таблице 2:
1). Полное сопротивление цепи Z;
2). Напряжение U, приложенное к цепи;
3). Ток I;
4). Угол сдвига фаз j (по величине и знаку);
5). Активную P, реактивную Q и полную S мощности, потребляемые цепью.
Начертить в масштабе векторную диаграмму и кратко пояснить её построение.
Подсчитать величину полного сопротивления цепи при увеличении частоты тока f в два раза.
Каковы условия для наступления в цепи резонанса напряжений и чему будет равен ток при резонансе.
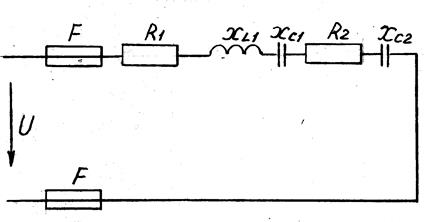
Рисунок 10
Таблица 2
| № вар. | R1, Ом | R2, Ом | xL1, Ом | xC1, Ом | xC2, Ом | Дополнительный параметр |
| 1. | Q= -192 (ВАр) | |||||
| 2. | UR2=20 (В) | |||||
| 3. | QL1= 16 (ВАр) | |||||
| 4. | UC1= 40 (В) | |||||
| 5. | S= 80 (BA) | |||||
| 6. | P= 45 (Вт) | |||||
| 7. | U= 68 (В) | |||||
| 8. | I= 4 (A) | |||||
| 9. | UL1= 12 (В) | |||||
| 10. | PR1= 150 (Вт) |
Методические указания решения задачи 2
|
|
|

Рисунок 11
Исходные данные:
Источник U=110B; f=50Гц питает цепь из последовательно включённых элементов R=10 Ом, C=150мкФ, L=50мГн.
Определить: I, UR, UL, UC, P, Q, S.
Построить векторную диаграмму.
Решение:
1. Определяем индуктивное сопротивление катушки.
xL =2π fL = 2·3,14·50·50·10-3=15,7(Ом).
2. Определяем емкостное сопротивление конденсатора.
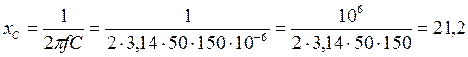 (Ом)
(Ом)
3. Определяем полное сопротивление цепи:
 Ом
Ом
4. Определяем силу тока цепи:
 А
А
5. Определяем активную мощность цепи:
а)  Вт
Вт
б) P=UI·cosφ = 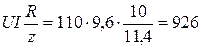 Вт
Вт
6. Определяем реактивную мощность цепи:
а)  ВАр
ВАр
б) Q = UI·sinφ = 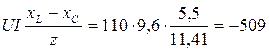 ВАр
ВАр
7. Определяем полную мощность цепи:
а) S=I2·z= 9,62·11,41=1051,5 ВА
б) S=UI= 110·9,6=1056 BA
Для построения векторной диаграммы определяем напряжения на участках:
UR=I · R= 9,6·10=96 В
UL=I · xL= 9,6·15,7=150,7 В
UC=I · xC= 9,6·21,2=203,5 В
Для построения выбираем масштаб:
1 см = 20 В
| Значение напряжения | Значение по оси х, см | Значение по оси y, см |
| UR= 96 В | 4,8 | |
| UL= 150,7 В | 7,5 | |
| UC= 203,5 В | 10,2 |
|
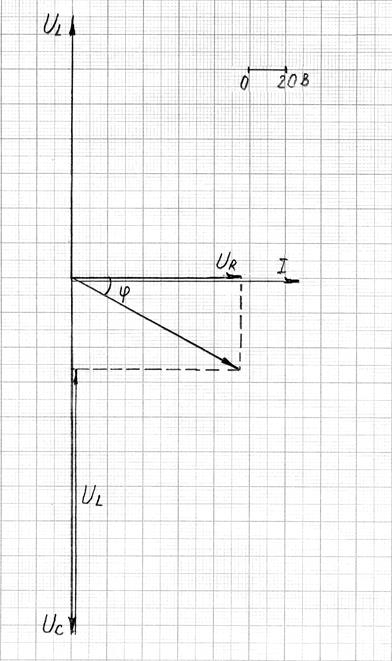
Рисунок 12 – Векторная диаграмма
Задача 3
Для электрической цепи переменного тока, изображенной на рисунке 13, определить токи в каждой ветви и в неразветвленной части цепи. Данные для своего варианта взять из таблицы 3. Составить баланс активных и реактивных мощностей. Задачу решить символическим методом. В масштабе построить векторную диаграмму цепи в комплексной системе координат. Вычертить схему цепи, учитывая характер нагрузки на всех ее участках (см. таблицу 3). Прочерк в таблице 3 означает отсутствие данного сопротивления в схеме цепи.
Таблица 3
| № вар. | U, В | R1,Ом | x1, Ом | R2,Ом | x2, Ом | R3, Ом | x3, Ом |
| 1. | - | - | 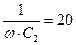
| 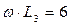
| |||
| 2. | - | 
| 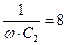
| - | |||
| 3. | - | 
| - | 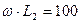
|  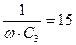
| ||
| 4. | - | 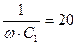
| - | 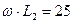
| 
| ||
| 5. | - | - | 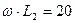
| 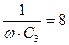
| |||
| 6. | - | 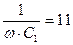
| - | 
| |||
| 7. | - | 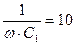
| - | 
| 
| ||
| 8. | 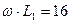
| - | 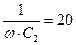
| - | |||
| 9. | - | 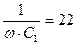
| - | 
| |||
| 10. | - | - |  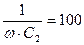
| 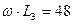
|
|
|
|
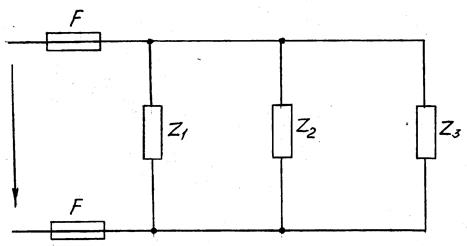
Рисунок 13
Методические указания решения задачи 3
Решение символическим методом,
Т.е при помощи комплексных чисел
 |
Рисунок 14
Законы параллельного соединения:
U – одинаково;

Записываем параметры цепи в форме комплексных чисел.
 Ом
Ом
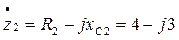 Ом
Ом
|
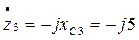 Ом
Ом
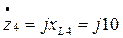 Ом
Ом
 Ом
Ом
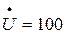 В
В
 А
А
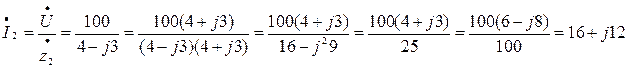 А
А
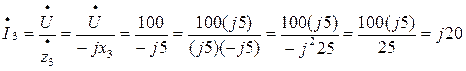 А
А
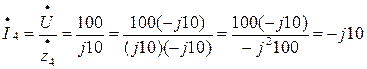 А
А
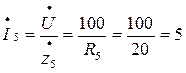 А
А
Находим Iобщ
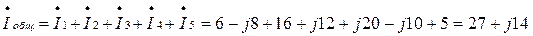 А
А
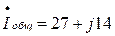 А
А
 ВА
ВА
P =2700 Вт
Q =-1400 ВАр – минус указывает на емкостной характер нагрузки
 ВА
ВА
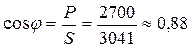
φ=arcos (0,888)=27,370
Векторную диаграмму строим на комплексной плоскости.
Для построения выбираем масштаб:
1 см = 1 А
| Значения токов | Значение по оси х, см | Значение по оси y, см |
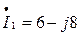 А А
| 1,5 | |
 А А
| ||
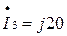 А А
| ||
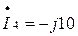 А А
| -2,5 | |
 А А
| 1,25 |
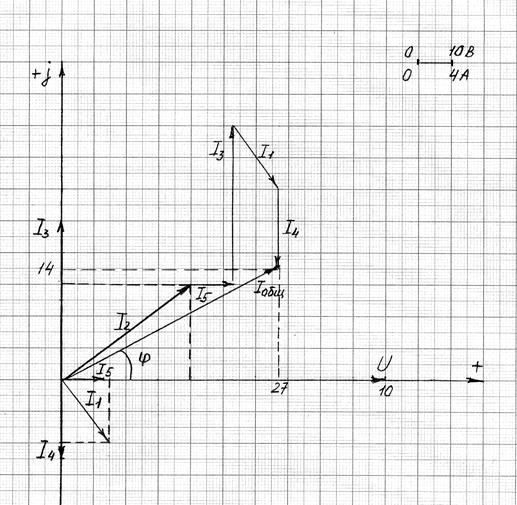
Рисунок 15
Задача 4
На рисунке 16 показана трехфазная сеть, питающая две нагрузки, одна из которых соединена звездой, другая – треугольником. Система линейных напряжений симметрична (UAB= UBC= UCA = U).
Определить:
- фазные и линейные токи нагрузок;
- токи в проводах линии, питающей обе нагрузки;
- ток в нейтральном проводе;
- активную и реактивную мощности каждой из нагрузок и всей установки.
В масштабе построить векторную диаграмму токов и напряжений. Задачу решить графо – аналитическим методом. Данные для своего варианта взять из таблицы 4.
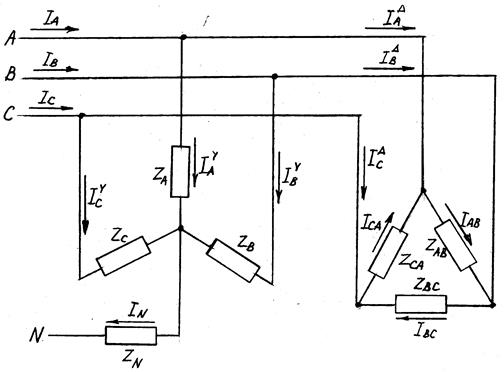
Рисунок 16
 Таблица 4
Таблица 4
| Варианты | U, В | Приемник энергии, соединенный звездой | Приемник энергии, соединенный треугольником | |||||||
| zN, Ом | мощности фаз и коэффициент мощности | мощности фаз и коэффициент мощности | ||||||||
| PA, Вт | PB, Вт | PC, Вт | Cos jY | PAB, Вт | PBC, Вт | PCA, Вт | Cos j∆ | |||
| 0,866 | ||||||||||
| ∞ | 0,8 | |||||||||
| ∞ | 0,866 | |||||||||
| 0,8 | ||||||||||
| ∞ | 0,5 | |||||||||
| 0,5 | ||||||||||
| 0,6 | ||||||||||
| ∞ | 0,707 | |||||||||
| ∞ | 0,6 | |||||||||
| 0,707 |
|
|
|