 |
Вспомогательный лист к частотным характеристикам
|
|
|
|
1-24 вопросы общего характера – могут даваться по 2 в задании.
Вопросы 25-33 (9 шт.) – характеристики отдельных звеньев
Вопросы 34-56 – ЛАФЧХ соединений
Устойчивость.
Общие вопросы и D –разбиение.
№1
В устойчивой системе:
1. Реакция на любое воздействие ограничена.
2. Реакция на любое ограниченное воздействие ограничена.
3. Реакция на неограниченное воздействие ограничена.
4.Найдется хотя бы одно ограниченное воздействие, реакция на которое неограниченна.
№2
Какое из приведенных ниже условий является необходимым и достаточным условием устойчивости линейной системы ( - передаточная функция,
- передаточная функция,  - переходная характеристика,
- переходная характеристика,  - импульсная переходная функция):
- импульсная переходная функция):
1.  для всех
для всех  3.
3. 
2.  4.
4.  для всех
для всех  :
:  .
.
№3
Какое из приведенных ниже условий является необходимым и достаточным условием устойчивости линейной системы ( - передаточная функция,
- передаточная функция,  - переходная характеристика,
- переходная характеристика,  - импульсная переходная функция):
- импульсная переходная функция):
1.  для всех
для всех  :
: 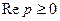 3.
3. 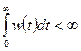
2.  4.
4.  для всех
для всех 
№4
Передаточная функция системы имеет вид: 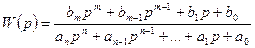 . Характеристическое уравнение данной системы имеет вид:
. Характеристическое уравнение данной системы имеет вид:
1. 
2. 
3. 
4. 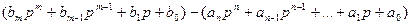 =0.
=0.
№5
Для того, чтобы система была устойчивой, корни характеристического уравнения  должны удовлетворять условию:
должны удовлетворять условию:
1. 
 3.
3. 

2. 
 4.
4. 
 .
.
№6
Заданы 4 набора значений корней характеристического уравнения. Указать, какой набор корней соответствует устойчивой системе:
1. 


2. 


3. 


4. 

 .
.
№7
Заданы 4 набора значений корней характеристического уравнения. Указать, какой набор корней соответствует устойчивой системе:
1. 
2. 
3. 
4. 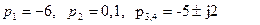 .
.
№8
Заданы 4 набора значений корней характеристического уравнения. Указать, какой набор корней соответствует устойчивой системе:
|
|
|
1. 
2. 
3. 
4.  .
.
№9
Из приведенных характеристических уравнений, не решая их, выделить уравнение, соответствующее заведомо неустойчивой системе:
1. 
2. 
3. 
4. 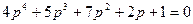 .
.
№10
Из приведенных характеристических уравнений, не решая их, выделить уравнение, соответствующее заведомо неустойчивой системе:
1. 
2. 
3. 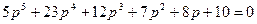
4.  .
.
№11
Из приведенных характеристических уравнений, не решая их, выделить уравнение, соответствующее заведомо неустойчивой системе:
1. 
2. 
3. 
4.  .
.
№12
Выделить верное утверждение:
1. Если коэффициенты характеристического уравнения имеют одинаковые знаки, то система устойчива.
2. Если система устойчива, то коэффициенты характеристического уравнения имеют одинаковые знаки.
3. Если характеристическое уравнение не имеет кратных корней, то система устойчива.
4. Если система неустойчива, то коэффициенты характеристического уравнения имеют различные знаки.
№13
Выделить неверное утверждение:
1.Если система устойчива, то коэффициенты характеристического уравнения имеют одинаковые знаки.
2. Если коэффициенты характеристического уравнения имеют различные знаки, то система неустойчива.
3. Если коэффициенты характеристического уравнения имеют одинаковые знаки, то система устойчива.
4. Для системы второго порядка положительность коэффициентов характеристического уравнения является необходимым и достаточным условием устойчивости.
№14
Выделить неверное утверждение:
1. Для систем 2-го порядка положительность коэффициентов характеристического уравнения является достаточным условием устойчивости.
2. Для систем 2-го порядка положительность коэффициентов характеристического уравнения является необходимым условием устойчивости.
3. Для систем 3-го и более высоких порядков положительность коэффициентов характеристического уравнения является достаточным условием устойчивости.
4. Для систем 3-го и более высоких порядков положительность коэффициентов характеристического уравнения является необходимым условием устойчивости.
|
|
|
№15
Структурная схема системы имеет вид:
 .
.
Характеристическое уравнение этой системы имеет вид:
1. 
2. 
3. 
4.  .
.
№16
При проведении D-разбиения решается задача:
1. Анализа устойчивости при заданных параметрах системы.
2. Выделение областей устойчивости в пространстве параметров системы.
3. Выделение областей равных значений корней характеристического уравнения в пространстве параметров системы.
4. Выделение областей действительных значений корней характеристического уравнения в пространстве параметров системы.
№17
Если при проведении D-разбиения в пространстве D точка находится на поверхности, разделяющей области  и
и  , то при этом один из корней характеристического уравнения:
, то при этом один из корней характеристического уравнения:
1. Находится на единичной окружности.
2. Находится на действительной оси
3. Находится на мнимой оси.
4. Находится в бесконечно удаленной точке.
№18
Передаточная функция разомкнутой САУ имеет вид:  . Характеристическое уравнение замкнутой системы с единичной обратной связью имеет вид:
. Характеристическое уравнение замкнутой системы с единичной обратной связью имеет вид:
1.  3.
3. 
2.  4.
4.  .
.
№19
Передаточная функция замкнутой САУ по ошибке имеет вид:  . Характеристическое уравнение замкнутой системы имеет вид:
. Характеристическое уравнение замкнутой системы имеет вид:
1. 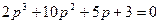 3.
3. 
2.  4.
4. 
№20
Дифференциальное уравнение системы имеет вид:  . Характеристическое уравнение для анализа устойчивости данной системы имеет вид:
. Характеристическое уравнение для анализа устойчивости данной системы имеет вид:
1.  3.
3. 
2.  4.
4.  .
.
№21
Дифференциальное уравнение системы имеет вид:  . Характеристическое уравнение для анализа устойчивости данной системы имеет вид:
. Характеристическое уравнение для анализа устойчивости данной системы имеет вид:
1.  3.
3. 
2.  4.
4.  .
.
№22
Дифференциальное уравнение системы имеет вид:  . Характеристическое уравнение для анализа устойчивости данной системы имеет вид:
. Характеристическое уравнение для анализа устойчивости данной системы имеет вид:
1. 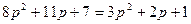 3.
3. 
2. 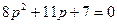 4.
4.  .
.
№23
Передаточная функция разомкнутой САУ имеет вид:  . Характеристическое уравнение замкнутой системы с единичной обратной связью имеет вид:
. Характеристическое уравнение замкнутой системы с единичной обратной связью имеет вид:
1.  3.
3. 
2.  4.
4. 
№24
В устойчивой линейной системе:
1. Любому входному сигналу всегда соответствует ограниченная реакция системы.
2. Можно подобрать ограниченный входной сигнал, реакция на который будет неограниченной.
3. Собственные движения системы всегда ограничены.
|
|
|
4. Можно подобрать неограниченный входной сигнал, реакция на который будет ограниченной.
№25
Передаточная функция системы имеет вид: 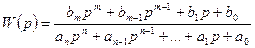 . Система заведомо неустойчива, если:
. Система заведомо неустойчива, если:
1.  3.
3. 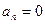
2.  4.
4.  .
.
Алгебраические критерии устойчивости.
№26
Критерий Рауса является:
1. Необходимым и достаточным условием устойчивости.
2. Только необходимым условием устойчивости.
3. Только достаточным условием устойчивости.
№27
Характеристическое уравнение системы имеет вид: 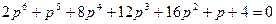 . Третья сверху строка таблицы Рауса для этого случая имеет вид:
. Третья сверху строка таблицы Рауса для этого случая имеет вид:
1.
2.
| -14 |
3.
| -16 |
4.
| -16 | -14 |
№28
Характеристическое уравнение системы имеет вид: 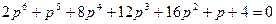 . Третий слева направо столбец определителя Гурвица для этого случая имеет вид:
. Третий слева направо столбец определителя Гурвица для этого случая имеет вид:
1. 4 2. 1 3. 1 4. 1
1 16 16 4
16 12 12 16
12 8 8 12
8 1 2 8
2 2 0 2
№29
Характеристическое уравнение системы имеет вид: 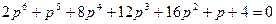 . Будет ли устойчивой данная система:
. Будет ли устойчивой данная система:
1. Да
2. Нет.
№30
Характеристическое уравнение системы имеет вид:  . Определитель Гурвица для этого уравнения имеет вид:
. Определитель Гурвица для этого уравнения имеет вид:
1.  2.
2.  3.
3. 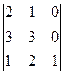 4.
4. 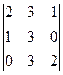 .
.
№31
Характеристическое уравнение системы имеет вид:  . При каких значениях параметра
. При каких значениях параметра  система будет устойчивой:
система будет устойчивой:
1.  2.
2. 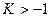 3.
3.  4.
4.  .
.
№32
Характеристическое уравнение системы имеет вид:  . При каких значениях параметра
. При каких значениях параметра  система будет устойчивой:
система будет устойчивой:
1.  3.
3. 
2.  4.
4.  .
.
№33
Передаточная функция разомкнутой системы равна  . При каких значениях
. При каких значениях  будет устойчива система, полученная замыканием данной передаточной функции единичной обратной связью:
будет устойчива система, полученная замыканием данной передаточной функции единичной обратной связью:
1. 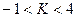 3.
3. 
2.  4.
4.  .
.
№34
Характеристическое уравнение системы имеет вид:  . Четвертая сверху строка таблицы Рауса для этого случая имеет вид:
. Четвертая сверху строка таблицы Рауса для этого случая имеет вид:
1.
2.
3.
| 1,5 | 1,5 |
4.
| 1,5 |
№35
Характеристическое уравнение системы имеет вид:  . Будет ли устойчивой данная система:
. Будет ли устойчивой данная система:
1. Да
2. Нет.
№36
Характеристическое уравнение системы имеет вид:  . Определитель Гурвица для этого уравнения имеет вид:
. Определитель Гурвица для этого уравнения имеет вид:
1.  2.
2.  3.
3.  4.
4. 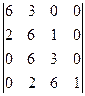
№37
Характеристическое уравнение системы имеет вид:  . Третья сверху строка таблицы Рауса для этого случая имеет вид:
. Третья сверху строка таблицы Рауса для этого случая имеет вид:
|
|
|
1.
2.
3.
| 2/3 |
4.
№38
Характеристическое уравнение системы имеет вид:  . Первый диагональный минор определителя Гурвица для этого случая имеет вид:
. Первый диагональный минор определителя Гурвица для этого случая имеет вид:
1.  2.
2.  3.
3.  4.
4.  .
.
№39
Характеристическое уравнение системы имеет вид:  . Будет ли устойчивой данная система:
. Будет ли устойчивой данная система:
1. Да
2. Нет
№40
Критерий Гурвица является:
1. Необходимым и достаточным условием устойчивости.
2. Только необходимым условием устойчивости.
3. Только достаточным условием устойчивости.
№41
Характеристическое уравнение системы имеет вид:  . Определитель Гурвица для этого уравнения имеет вид:
. Определитель Гурвица для этого уравнения имеет вид:
1.  2.
2.  3.
3.  4.
4.  .
.
№42
Характеристическое уравнение системы имеет вид:  . Определитель Гурвица для этого уравнения имеет вид:
. Определитель Гурвица для этого уравнения имеет вид:
1.  2.
2.  3.
3.  4.
4.  .
.
№43
Характеристическое уравнение системы имеет вид:  . Определитель Гурвица для этого уравнения имеет вид:
. Определитель Гурвица для этого уравнения имеет вид:
1.  2.
2.  3.
3.  4.
4.  .
.
№44
Характеристическое уравнение системы 3-го порядка имеет вид:  . Необходимое и достаточное условие устойчивости для этого случая имеет вид:
. Необходимое и достаточное условие устойчивости для этого случая имеет вид:
1. 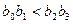 3.
3. 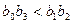
2.  4.
4.  .
.
№45
Передаточная функция разомкнутой системы имеет вид:  . Условие устойчивости замкнутой единичной обратной связью САУ имеет вид:
. Условие устойчивости замкнутой единичной обратной связью САУ имеет вид:
1.  3.
3. 
2.  4.
4.  .
.
№46
Передаточная функция разомкнутой системы равна  . При каких значениях
. При каких значениях  будет устойчива система, полученная замыканием данной передаточной функции единичной обратной связью:
будет устойчива система, полученная замыканием данной передаточной функции единичной обратной связью:
1.  3.
3. 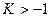 ?
?
2.  4.
4.  .
.
№47
Передаточная функция разомкнутой системы равна  . При каких значениях
. При каких значениях  будет устойчива система, полученная замыканием данной передаточной функции единичной обратной связью:
будет устойчива система, полученная замыканием данной передаточной функции единичной обратной связью:
1.  3.
3. 
2.  4.
4. 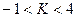 .
.
№48
Передаточная функция разомкнутой системы имеет вид:  . Условие устойчивости замкнутой единичной обратной связью САУ имеет вид:
. Условие устойчивости замкнутой единичной обратной связью САУ имеет вид:
1. 
2. 
3. 
4.  .
.
№49
Передаточная функция разомкнутой системы имеет вид:  . Условие устойчивости замкнутой единичной обратной связью САУ имеет вид:
. Условие устойчивости замкнутой единичной обратной связью САУ имеет вид:
1. 
2. 
3. 
4.  .
.
|
|
|


