 |
Тема 2. Множественная линейная регрессия
|
|
|
|
Правила выполнения и оформления контрольной работы
Студенты заочного факультета выполняют одну контрольную работу по эконометрике. Номер варианта задает преподаватель.
На титульном листе разборчиво написать фамилию и инициалы, название факультета, специальность и номер варианта. Перед решением задачи необходимо полностью написать ее условие. Решение задачи излагать подробно с объяснением всех действий.
После получения отрецензированной работы студент должен исправить все отмеченные ошибки или недочеты в той же тетради и явиться на собеседование или зачет. Если задача решена неверно, то студенту необходимо переделать ее или прислать работу на повторную рецензию.
На проверку принимаются только контрольные работы, выполненные по своему варианту и в соответствии с указанными требованиями.
Варианты контрольной работы по эконометрике
Тема 1. Парная линейная регрессия
Вариант 1
По 12 фирмам проводился анализ взаимосвязи следующих признаков: х ($) – цена товара А, у (тыс. ед.) – объем продаж данного товара. Признаки х и у имеют нормальный закон распределения.
| X | 0,3 | 1,2 | 1,3 | 1,5 | 1,4 | 1,6 | 2,1 | 2,5 | 2,8 | 2,7 | 2,9 | |
| Y | 5,8 | 4,6 | 5,2 | 4,2 | 4,5 | 3,4 | 3,6 | 2,4 | 2,5 | 2,4 | 2,8 |
Задание:
1. Постройте поле корреляции и сформулируйте гипотезу о форме связи между ценой товара А и объемом продаж данного товара.
2. Рассчитайте оценки параметров уравнения парной линейной регрессии.
3. Оцените тесноту связи между ценой товара А и объемом продаж данного товара с помощью выборочного коэффициента корреляции. Проверьте значимость коэффициента корреляции (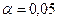
).
4. Рассчитайте выборочный коэффициент детерминации. Сделайте экономический вывод.
|
|
|
5. Проверьте значимость оценки коэффициента регрессии с помощью критерия Стьюдента при уровне значимости .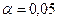
6. Постройте доверительный интервал для коэффициента регрессии. Дайте экономическую интерпретацию.
7. Составьте таблицу дисперсионного анализа.
8. Оцените с помощью F- критерия Фишера - Снедекора значимость уравнения линейной регрессии ().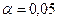
9. Рассчитайте объем продаж данного товара, если его цена составит 11 $. Постройте доверительный интервал для прогнозного значения объясняемой переменной. Сделайте экономический вывод.
10. Рассчитайте средний коэффициент эластичности (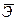
).Сделайте экономический вывод.
11. Определить среднюю ошибку аппроксимации.
12. На поле корреляции постройте линию регрессии.
Вариант 2
Имеются данные по 12 малым предприятиям города: х (тыс. $) – единовременные расходы на рекламу, у (тыс. $) – прибыль предприятия. Признаки х и у имеют нормальный закон распределения.
| X | 6,5 | 4,2 | 8,1 | 10,6 | 12,9 | 17,1 | 14,3 | 18,5 | 15,8 | 19,8 | 11,4 | |
| Y |
Задание:
1. Постройте поле корреляции и сформулируйте гипотезу о форме связи между расходами на рекламу и прибылью.
2. Рассчитайте оценки параметров уравнения парной линейной регрессии.
3. Оцените тесноту связи между расходами на рекламу и прибылью с помощью выборочного коэффициента корреляции. Проверьте значимость коэффициента корреляции (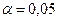
).
4. Рассчитайте выборочный коэффициент детерминации. Сделайте экономический вывод.
5. Проверьте значимость оценки коэффициента регрессии с помощью критерия Стьюдента при уровне значимости .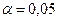
6. Постройте доверительный интервал для коэффициента регрессии. Дайте экономическую интерпретацию.
7. Составьте таблицу дисперсионного анализа.
8. Оцените с помощью F- критерия Фишера - Снедекора значимость уравнения линейной регрессии ().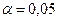
9. Рассчитайте прибыль малого предприятия, если расходы на рекламу будут равны 16 тыс. $. Постройте доверительный интервал для прогнозного значения объясняемой переменной. Сделайте экономический вывод.
|
|
|
10. Рассчитайте средний коэффициент эластичности (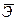).Сделайте экономический вывод.
11. Определить среднюю ошибку аппроксимации.
12. На поле корреляции постройте линию регрессии.
Вариант 3
Изучается зависимость между ценой квартиры (тыс. долл.) у и размером ее общей площади (м2) х.
| х | ||||||||||
| у |
Задание:
1. Постройте поле корреляции и сформулируйте гипотезу о форме связи между ценой квартиры и размером ее общей площади.
2. Рассчитайте оценки параметров уравнения парной линейной регрессии.
3. Оцените тесноту связи между признаками с помощью выборочного коэффициента корреляции. Проверьте значимость коэффициента корреляции (
).
4. Рассчитайте выборочный коэффициент детерминации. Сделайте экономический вывод.
5. Проверьте значимость оценки коэффициента регрессии с помощью критерия Стьюдента при уровне значимости .
6. Постройте доверительный интервал для коэффициента регрессии. Дайте экономическую интерпретацию.
7. Составьте таблицу дисперсионного анализа.
8. Оцените с помощью F- критерия Фишера - Снедекора значимость уравнения линейной регрессии ().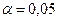
9. Рассчитайте цену квартиры, если общая площадь квартиры составит 50 м2. Постройте доверительный интервал для прогнозного значения объясняемой переменной. Сделайте экономический вывод.
10. Рассчитайте средний коэффициент эластичности (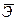). Сделайте экономический вывод.
11. Определить среднюю ошибку аппроксимации.
12. На поле корреляции постройте линию регрессии.
Вариант 4
Случайным образом были отобраны данные по 10 регионам. у (тыс. ед.)– характеризует годовой объем продаж некоторого продукта фирмы, а х (дес. тыс. долл.) – определяет годовые затраты на рекламу.
| х | ||||||||||
| у |
Задание:
1. Постройте поле корреляции и сформулируйте гипотезу о форме связи между признаками.
2. Рассчитайте оценки параметров уравнения парной линейной регрессии.
|
|
|
3. Оцените тесноту связи между признаками с помощью выборочного коэффициента корреляции. Проверьте значимость коэффициента корреляции ().
4. Рассчитайте выборочный коэффициент детерминации. Сделайте экономический вывод.
5. Проверьте значимость оценки коэффициента регрессии с помощью критерия Стьюдента при уровне значимости .
6. Постройте доверительный интервал для коэффициента регрессии. Дайте экономическую интерпретацию.
7. Составьте таблицу дисперсионного анализа.
8. Оцените с помощью F- критерия Фишера - Снедекора значимость уравнения линейной регрессии ().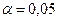
9. Рассчитайте годовой объем продаж, если годовые затраты на рекламу составят 65 дес. тыс. долл. Постройте доверительный интервал для прогнозного значения объясняемой переменной. Сделайте экономический вывод.
10. Рассчитайте средний коэффициент эластичности (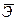). Сделайте экономический вывод.
11. Определить среднюю ошибку аппроксимации.
12. На поле корреляции постройте линию регрессии.
Вариант 5
По 12 предприятиям исследовали зависимость следующих признаков: х (тыс. $) – объем производства и у ($) – себестоимость единицы продукции. Признаки имеют нормальный закон распределения.
| х | ||||||||||||
| у | 42,4 | 35,5 | 36,5 | 25,3 | 29,8 | 22,1 | 19,7 | 18,2 | 16,5 | 13,9 | 12,5 | 11,1 |
Задание:
1. Постройте поле корреляции и сформулируйте гипотезу о форме связи между объемом производства и себестоимостью единицы продукции.
2. Рассчитайте оценки параметров уравнения парной линейной регрессии.
3. Оцените тесноту связи между объемом производства и себестоимостью с помощью выборочного коэффициента корреляции. Проверьте значимость коэффициента корреляции ().
4. Рассчитайте выборочный коэффициент детерминации. Сделайте экономический вывод.
5. Проверьте значимость оценки коэффициента регрессии с помощью критерия Стьюдента при уровне значимости .
6. Постройте доверительный интервал для коэффициента регрессии. Дайте экономическую интерпретацию.
7. Составьте таблицу дисперсионного анализа.
|
|
|
8. Оцените с помощью F- критерия Фишера - Снедекора значимость уравнения линейной регрессии ().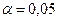
9. Рассчитайте себестоимость единицы продукции, если объем производства составит 13 тыс. $. Постройте доверительный интервал для прогнозного значения объясняемой переменной. Сделайте экономический вывод.
10. Рассчитайте средний коэффициент эластичности (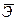). Сделайте экономический вывод.
11. Определить среднюю ошибку аппроксимации.
12. На поле корреляции постройте линию регрессии.
Вариант 6
Исследовали зависимость расходов на аренду жилья (у, тыс. р.) от среднемесячного дохода квартиросъемщика (х, тыс. р.) по 12 семьям. Признаки х и у имеют нормальный закон распределения.
| х | 6,5 | 4,2 | 8,1 | 13,2 | 10,6 | 17,1 | 14,3 | 7,2 | 26,7 | 23,2 | 16,6 | |
| у | 1,2 | 1,6 | 1,9 | 2,8 | 2,0 | 3,0 | 3,4 | 1,6 | 2,3 | 4,9 | 4,5 | 3,2 |
Задание:
1. Постройте поле корреляции и сформулируйте гипотезу о форме связи между среднемесячным доходом и расходами на аренду жилья.
2. Рассчитайте оценки параметров уравнения парной линейной регрессии.
3. Оцените тесноту связи между среднемесячным доходом и расходами на жилье с помощью выборочного коэффициента корреляции. Проверьте значимость коэффициента корреляции ().
4. Рассчитайте выборочный коэффициент детерминации. Сделайте экономический вывод.
5. Проверьте значимость оценки коэффициента регрессии с помощью критерия Стьюдента при уровне значимости .
6. Постройте доверительный интервал для коэффициента регрессии. Дайте экономическую интерпретацию.
7. Составьте таблицу дисперсионного анализа.
8. Оцените с помощью F- критерия Фишера - Снедекора значимость уравнения линейной регрессии ().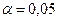
9. Рассчитайте расходы на аренду жилья, если среднемесячный доход составит 15 тыс. руб. Постройте доверительный интервал для прогнозного значения объясняемой переменной. Сделайте экономический вывод.
10. Рассчитайте средний коэффициент эластичности (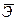). Сделайте экономический вывод.
11. Определить среднюю ошибку аппроксимации.
12. На поле корреляции постройте линию регрессии.
Вариант 7
По 11 объявлениям о продаже квартир получены следующие значения признаков: х (м2) – общая площадь квартиры, у (тыс. $) – цена квартиры. Признаки имеют нормальный закон распределения.
| х | |||||||||||
| у |
Задание:
1. Постройте поле корреляции и сформулируйте гипотезу о форме связи между общей площадью квартиры и ее ценой.
2. Рассчитайте оценки параметров уравнения парной линейной регрессии.
3. Оцените тесноту связи между признаками с помощью выборочного коэффициента корреляции. Проверьте значимость коэффициента корреляции ().
|
|
|
4. Рассчитайте выборочный коэффициент детерминации. Сделайте экономический вывод.
5. Проверьте значимость оценки коэффициента регрессии с помощью критерия Стьюдента при уровне значимости .
6. Постройте доверительный интервал для коэффициента регрессии. Дайте экономическую интерпретацию.
7. Составьте таблицу дисперсионного анализа.
8. Оцените с помощью F- критерия Фишера - Снедекора значимость уравнения линейной регрессии ().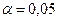
9. Рассчитайте цену квартиры, если площадь будет равна 50 м2. Постройте доверительный интервал для прогнозного значения объясняемой переменной. Сделайте экономический вывод.
10. Рассчитайте средний коэффициент эластичности (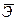). Сделайте экономический вывод.
11. Определить среднюю ошибку аппроксимации.
12. На поле корреляции постройте линию регрессии.
Вариант 8
По 11 семьям получены следующие данные: х (тыс. р.) – среднемесячный доход, у (тыс. р.) – расходы на питание и непродовольственные товары. Признаки имеют нормальный закон распределения.
| х | 9,7 | 10,1 | 13,3 | 17,4 | 4,5 | 7,2 | 5,9 | 7,7 | 6,4 | 10,6 | |
| у | 8,2 | 6,9 | 8,2 | 7,5 | 8,4 | 2,5 | 4,7 | 3,1 | 6,2 | 3,4 | 8,4 |
Задание:
1. Постройте поле корреляции и сформулируйте гипотезу о форме связи между среднемесячным доходом и расходами на питание и непродовольственные товары.
2. Рассчитайте оценки параметров уравнения парной линейной регрессии.
3. Оцените тесноту связи между признаками с помощью выборочного коэффициента корреляции. Проверьте значимость коэффициента корреляции ().
4. Рассчитайте выборочный коэффициент детерминации. Сделайте экономический вывод.
5. Проверьте значимость оценки коэффициента регрессии с помощью критерия Стьюдента при уровне значимости .
6. Постройте доверительный интервал для коэффициента регрессии. Дайте экономическую интерпретацию.
7. Составьте таблицу дисперсионного анализа.
8. Оцените с помощью F- критерия Фишера - Снедекора значимость уравнения линейной регрессии ().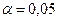
9. Рассчитайте расходы на питание и непродовольственные товары, если среднемесячный доход составит 9 тыс. р. Постройте доверительный интервал для прогнозного значения объясняемой переменной. Сделайте экономический вывод.
10. Рассчитайте средний коэффициент эластичности (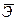). Сделайте экономический вывод.
11. Определить среднюю ошибку аппроксимации.
12. На поле корреляции постройте линию регрессии.
Вариант 9
По 12 предприятиям исследовали зависимость следующих признаков: х (тыс. $) – расходы на рекламу в СМИ и у (млн. $) – прибыль предприятия. Признаки имеют нормальный закон распределения.
| х | 6,5 | 4,2 | 8,8 | 10,6 | 15,9 | 17,1 | 14,3 | 18,5 | 19,6 | 20,4 | 12,7 | |
| у | 9,4 | 10,6 | 14,6 | 16,7 | 19,6 | 22,5 | 25,7 | 26,3 | 13,6 |
Задание:
1. Постройте поле корреляции и сформулируйте гипотезу о форме связи между расходами на рекламу в СМИ и прибылью предприятия.
2. Рассчитайте оценки параметров уравнения парной линейной регрессии.
3. Оцените тесноту связи между признаками с помощью выборочного коэффициента корреляции. Проверьте значимость коэффициента корреляции ().
4. Рассчитайте выборочный коэффициент детерминации. Сделайте экономический вывод.
5. Проверьте значимость оценки коэффициента регрессии с помощью критерия Стьюдента при уровне значимости .
6. Постройте доверительный интервал для коэффициента регрессии. Дайте экономическую интерпретацию.
7. Составьте таблицу дисперсионного анализа.
8. Оцените с помощью F- критерия Фишера - Снедекора значимость уравнения линейной регрессии ().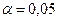
9. Рассчитайте прибыль предприятия, если расходы на рекламу будут равны 15 тыс. $. Постройте доверительный интервал для прогнозного значения объясняемой переменной. Сделайте экономический вывод.
10. Рассчитайте средний коэффициент эластичности (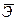). Сделайте экономический вывод.
11. Определить среднюю ошибку аппроксимации.
12. На поле корреляции постройте линию регрессии.
Вариант 10
Получены данные по 13 компаниям холдинга: х (тыс. $) – расходы на маркетинговые исследования, а у (млн. $) – прибыль компании. Признаки имеют нормальный закон распределения.
| х | 4,1 | 7,1 | 8,5 | 10,8 | 11,5 | 13,7 | 12,3 | 14,8 | 13,4 | 15,4 | 16,3 | 14,9 | 16,7 |
| у | 1,5 | 2,4 | 3,8 | 4,3 | 6,3 | 7,9 | 8,4 | 6,6 | 9,4 | 10,5 |
Задание:
1. Постройте поле корреляции и сформулируйте гипотезу о форме связи между расходами на маркетинговые исследования и прибылью компании.
2. Рассчитайте оценки параметров уравнения парной линейной регрессии.
3. Оцените тесноту связи между признаками с помощью выборочного коэффициента корреляции. Проверьте значимость коэффициента корреляции ().
4. Рассчитайте выборочный коэффициент детерминации. Сделайте экономический вывод.
5. Проверьте значимость оценки коэффициента регрессии с помощью критерия Стьюдента при уровне значимости .
6. Постройте доверительный интервал для коэффициента регрессии. Дайте экономическую интерпретацию.
7. Составьте таблицу дисперсионного анализа.
8. Оцените с помощью F- критерия Фишера - Снедекора значимость уравнения линейной регрессии ().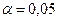
9. Рассчитайте прибыль компании, если расходы на маркетинговые исследования составят 10 тыс. $. Постройте доверительный интервал для прогнозного значения объясняемой переменной. Сделайте экономический вывод.
10. Рассчитайте средний коэффициент эластичности (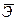). Сделайте экономический вывод.
11. Определить среднюю ошибку аппроксимации.
12. На поле корреляции постройте линию регрессии.
Тема 2. Множественная линейная регрессия
Вариант 1
В процессе изучения зависимости прибыли (тыс. руб.) у от выработки продукции на одного работника (ед.) х1 и индекса цен на продукцию (%) х2 получены данные по 30 предприятиям.
| Признак | Среднее значение | Среднее квадратическое отклонение | Парный коэффициент корреляции |
| у | 
| ||
| х1 | 
| ||
| х2 | 
|
Задание:
1. Построить уравнение множественной линейной регрессии в стандартизованном масштабе и в естественной форме.
2. Рассчитайте частные коэффициенты эластичности.
3. Рассчитать линейные коэффициенты частной корреляции и коэффициент множественной корреляции.
4. Оцените значимость уравнения регрессии в целом с помощью F – критерия Фишера.
Вариант 2
По 30 заводам, выпускающим продукцию А, изучается зависимость потребления электроэнергии (тыс. кВт ч) у от производства продукции (тыс. ед.) х1 и уровня механизации труда (%) х2. Данные приведены в таблице.
| Признак | Среднее значение | Среднее квадратическое отклонение | Парный коэффициент корреляции |
| у | 
| ||
| х1 | 
| ||
| х2 | 41,5 | 
|
Задание:
1. Построить уравнение множественной линейной регрессии в стандартизованном масштабе и в естественной форме.
2. Рассчитайте частные коэффициенты эластичности.
3. Рассчитать линейные коэффициенты частной корреляции и коэффициент множественной корреляции.
4. Оцените значимость уравнения регрессии в целом с помощью F – критерия Фишера.
Вариант 3
При изучении зависимости потребления материалов (т) у от энерговооруженности труда (кВтч на одного рабочего) х1 и объема произведенной продукции (тыс. ед.) х2 по 25 предприятиям получены следующие данные.
| Признак | Среднее значение | Среднее квадратическое отклонение | Парный коэффициент корреляции |
| у | 
| ||
| х1 | 4,3 | 0,5 | 
|
| х2 | 10,0 | 1,8 |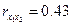 
|
Задание:
1. Построить уравнение множественной линейной регрессии в стандартизованном масштабе и в естественной форме.
2. Рассчитайте частные коэффициенты эластичности.
3. Рассчитать линейные коэффициенты частной корреляции и коэффициент множественной корреляции.
4. Оцените значимость уравнения регрессии в целом с помощью F – критерия Фишера.
Вариант 4
При изучении зависимости потребления материалов (т) у от энерговооруженности труда (кВтч на одного рабочего) х1 и объема произведенной продукции (тыс. ед.) х2 по 25 предприятиям получены следующие данные.
| Признак | Среднее значение | Среднее квадратическое отклонение | Парный коэффициент корреляции |
| у |
| ||
| х1 | 4,8 |
| |
| х2 | 0,8 | 
|
Задание:
1. Построить уравнение множественной линейной регрессии в стандартизованном масштабе и в естественной форме.
2. Рассчитайте частные коэффициенты эластичности.
3. Рассчитать линейные коэффициенты частной корреляции и коэффициент множественной корреляции.
4. Оцените значимость уравнения регрессии в целом с помощью F – критерия Фишера.
Вариант 5
При изучении зависимости потребления материалов (т) у от энерговооруженности труда (кВтч на одного рабочего) х1 и объема произведенной продукции (тыс. ед.) х2 по 25 предприятиям получены следующие данные.
| Признак | Среднее значение | Среднее квадратическое отклонение | Парный коэффициент корреляции |
| у |
| ||
| х1 | 4,3 | 0,5 |
|
| х2 | 10,0 | 1,8 |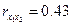
|
Задание:
1. Построить уравнение множественной линейной регрессии в стандартизованном масштабе и в естественной форме.
2. Рассчитайте частные коэффициенты эластичности.
3. Рассчитать линейные коэффициенты частной корреляции и коэффициент множественной корреляции.
4. Оцените значимость уравнения регрессии в целом с помощью F – критерия Фишера.
Вариант 6
В процессе изучения влияния климатических условий на урожайность зерновых (ц/га) у по 25 территориям страны были отобраны две объясняющие переменные:
х1 – количество осадков в период вегетации (мм);
х2 – средняя температура воздуха (0С).
| Признак | Среднее значение | Среднее квадратическое отклонение | Парный коэффициент корреляции |
| у |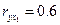 
| ||
| х1 | 
| ||
| х2 |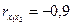 
|
Задание:
1. Построить уравнение множественной линейной регрессии в стандартизованном масштабе и в естественной форме.
2. Рассчитайте частные коэффициенты эластичности.
3. Рассчитать линейные коэффициенты частной корреляции и коэффициент множественной корреляции.
4. Оцените значимость уравнения регрессии в целом с помощью F – критерия Фишера.
Вариант 7
По 25 странам изучается зависимость индекса человеческого развития у от переменных:
х1 – валовое накопление, % к ВВП;
х2 – суточная калорийность питания населения, ккал на душу населения.
| Признак | Среднее значение | Среднее квадратическое отклонение | Парный коэффициент корреляции |
| у | 0,85 | 0,1 | 
|
| х1 | 21,74 | 5,6 | 
|
| х2 | 3179,24 | 321,6 |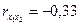 
|
Задание:
1. Построить уравнение множественной линейной регрессии в стандартизованном масштабе и в естественной форме.
2. Рассчитайте частные коэффициенты эластичности.
3. Рассчитать линейные коэффициенты частной корреляции и коэффициент множественной корреляции.
4. Оцените значимость уравнения регрессии в целом с помощью F – критерия Фишера.
Вариант 8
По 25 странам изучается зависимость индекса человеческого развития у от переменных:
х1 - суточная калорийность питания населения, ккал на душу населения;
х2 – ожидаемая продолжительность жизни при рождении 2003 г., число лет.
| Признак | Среднее значение | Среднее квадратическое отклонение | Парный коэффициент корреляции |
| у | 0,85 | 0,1 | 
|
| х1 | 3179,24 | 321,6 | 
|
| х2 | 74,42 | 4,8 | 
|
Задание:
1. Построить уравнение множественной линейной регрессии в стандартизованном масштабе и в естественной форме.
2. Рассчитайте частные коэффициенты эластичности.
3. Рассчитать линейные коэффициенты частной корреляции и коэффициент множественной корреляции.
4. Оцените значимость уравнения регрессии в целом с помощью F – критерия Фишера.
Вариант 9
По 25 странам изучается зависимость индекса человеческого развития у от переменных:
х1 – валовое накопление, % к ВВП;
х2 – ожидаемая продолжительность жизни при рождении 2003 г., число лет.
| Признак | Среднее значение | Среднее квадратическое отклонение | Парный коэффициент корреляции |
| у | 0,85 | 0,1 |
|
| х1 | 21,74 | 5,612 |
|
| х2 | 74,42 | 4,8 |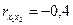 
|
Задание:
1. Построить уравнение множественной линейной регрессии в стандартизованном масштабе и в естественной форме.
2. Рассчитайте частные коэффициенты эластичности.
3. Рассчитать линейные коэффициенты частной корреляции и коэффициент множественной корреляции.
4. Оцените значимость уравнения регрессии в целом с помощью F – критерия Фишера.
Вариант 10
По 25 странам изучается зависимость индекса человеческого развития у от переменных:
х1 – валовое накопление, % к ВВП;
х2 – расходы домашних хозяйств, % к ВВП.
| Признак | Среднее значение | Среднее квадратическое отклонение | Парный коэффициент корреляции |
| у | 0,85 | 0,1 |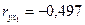 
|
| х1 | 21,74 | 5,61 |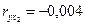 
|
| х2 | 58,74 | 6,07 | 
|
Задание:
1. Построить уравнение множественной линейной регрессии в стандартизованном масштабе и в естественной форме.
2. Рассчитайте частные коэффициенты эластичности.
3. Рассчитать линейные коэффициенты частной корреляции и коэффициент множественной корреляции.
4. Оцените значимость уравнения регрессии в целом с помощью F – критерия Фишера.
Приложение 1
|
|
|
