 |
Тема 1. Парная линейная регрессия
|
|
|
|
1. Рассчитайте оценки параметров парной линейной регрессии, где у – расходы на покупку продовольственных товаров, % к общему объему расходов, а х – среднемесячная заработная плата 1 работника, тыс. руб.
Параметры а и b линейной регрессии 
рассчитываются в результате решения системы нормальных уравнений относительно а и b:
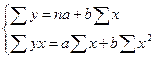
По исходным данным рассчитаем 
.
Система нормальных уравнений составит:
Решаем ее методом определителей: определитель системы ∆ равен:
,
,
, 
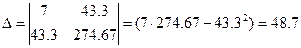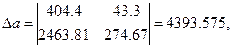
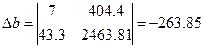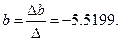
Получаем уравнение регрессии: 
.
Этот же результат можно получить, используя следующие формулы для нахождения параметров:
, 
,
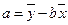где 
- дисперсия по факторному признаку.
Таблица 1. – Расчетные данные
| Номер региона | х | у | ху | 
| 
| 
| у-
|
| 4,5 | 68,8 | 309,6 | 20,25 | 4733,44 | 67,1 | 1,7 | |
| 5,9 | 58,3 | 343,97 | 34,81 | 3398,89 | 59,3 | -1,0 | |
| 5,7 | 62,6 | 356,82 | 32,49 | 3918,76 | 60,4 | 2,2 | |
| 7,2 | 52,1 | 375,12 | 51,84 | 2714,41 | 52,2 | -0,1 | |
| 6,2 | 54,5 | 337,9 | 38,44 | 2970,25 | 57,7 | -3,2 | |
| 57,1 | 342,6 | 3260,41 | 58,8 | -1,7 | |||
| 7,8 | 397,8 | 60,84 | 2601,00 | 48,9 | 2,1 | ||
| Сумма | 43,3 | 404,4 | 2463,81 | 274,67 | 23597,16 | 404,4 | |
| Среднее значение | 6,186 | 57,77 | 351,97 | 39,24 | 3371,02 | - | - |
Продолжение таблицы 1
| Номер региона | у-
| 
| 
| 
| 
| 
|
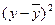
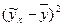
| 1,7 | 2,97 | 121,629 | 86,583 | 2,84 | 2,47 | |
| -1,0 | 1,10 | 0,279 | 2,487 | 0,08 | 1,72 | |
| 2,2 | 4,61 | 23,315 | 7,189 | 0,24 | 0,51 | |
| -0,1 | 0,01 | 32,165 | 31,346 | 1,03 | 0,19 | |
| -3,2 | 10,19 | 10,702 | 0,006 | 0,00 | 5,87 | |
| -1,7 | 2,88 | 0,451 | 1,051 | 0,03 | 2,98 | |
| 2,1 | 4,58 | 45,852 | 79,399 | 2,61 | 4,12 | |
| Сумма | 26,33 | 234,39 | 208,06 | 6,83 | 20,86 | |
| Среднее значение | - | - | - | - | - | - |
Однако, оперируя средними величинами, мы можем столкнуться с ошибками округления. Действительно,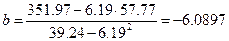 
. Соответственно не совпадает и величина параметра 
, т.е. 
При решении с помощью компьютера уравнение регрессии составило: 
.
Величина коэффициента регрессии 
означает, что с ростом заработной платы на 1 тыс. руб. доля расходов на покупку продовольственных товаров снижается в среднем на 5.5 % - х пункта.
|
|
|
2. Оцените тесноту связи между признаками.
Линейное уравнение регрессии дополняется расчетом линейного коэффициента корреляции:
или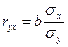 
.
Так как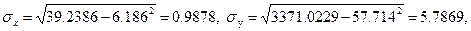 
то 
, что означает тесную обратную связь рассматриваемых признаков.
3. Рассчитайте коэффициент детерминации.
Коэффициент детерминации составит: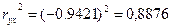 
, т.е. вариация у на 88,8 % объясняется вариацией х. На долю прочих факторов, не учитываемых в регрессии, приходится 11,2 %.
4. Проверьте значимость оценки коэффициента регрессии с помощью критерия Стьюдента при уровне значимости α=0,05.
Оценку статистической значимости коэффициента регрессии проведем с помощью t - критерия Стьюдента.
Выдвигаем две гипотезы:
Н0 – коэффициент регрессии является статистически незначимым, т.е. b=0;
Н1 – коэффициент регрессии статистически значим, т.е. b≠0.
Определим стандартную ошибку для коэффициента регрессии mb:
.
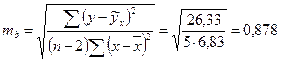Далее вычисляем значения t – критерия Стьюдента:
.
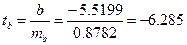Фактическое значение t – критерии превосходит табличное значение на 5 %-м уровне значимости при числе степеней свободы 
=5: tтабл = 2,57. Поэтому гипотеза Н0 отклоняется, т.е. b отличается от нуля не случайно и коэффициент регрессии является статистически значимым.
5. Постройте доверительный интервал для коэффициента регрессии.
Рассчитаем доверительный интервал для коэффициента регрессии, для чего определим предельную ошибку для параметра b.
.
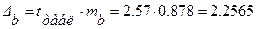Доверительные интервалы: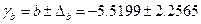 
, т.е.
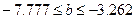
Анализ верхней и нижней границ доверительного интервала приводит к выводу о том, что с вероятностью 95% коэффициент регрессии, находясь в указанных границах, не принимает нулевых значение, т.е. не является статистически незначимым и существенно отличен от нуля.
6. Составить таблицу дисперсионного анализа.
Результаты дисперсионного анализа приведены в таблице 2.
|
|
|
Таблица 2. – Таблица дисперсионного анализа
| Вариация результата | Число степеней свободы | Сумма квадратов отклонений | Дисперсия на одну степень свободы | F - критерий | |
| факт. | табл. | ||||
| Общая | 234,39 | ||||
| Факторная | 208,06 | 208,06 | 39,5 | 6,61 | |
| Остаточная | 26,33 | 5,27 |
7. Оцените с помощью F – критерия Фишера-Снедекора значимость уравнения линейной регрессии.
В силу того, что Fфакт=39,5> Fтабл=6,61, гипотеза о случайности различий факторной и остаточной дисперсий отклоняется. Эти различия существенны, статистически значимы, уравнение значимо, показатель тесноты связи надежен и отражает устойчивую зависимость расходов на покупку продовольственных товаров от среднемесячной заработной платы.
8. Рассчитайте, каковы будут расходы на покупку продовольственных товаров, если среднемесячная заработная плата составит 8 тыс. руб.
Полученные оценки уравнения регрессии позволяют использовать его для прогноза. Если примем прогнозное значение среднемесячной заработной платы х=8, то точечный прогноз расходов составит: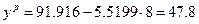 
% - х пункта.
Чтобы получить интервальный прогноз, найдем стандартную ошибку предсказываемого значения расходов 
.
;
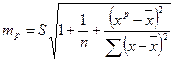где 
- стандартная ошибка регрессии.
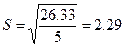
Предельная ошибка прогнозируемого расхода составит:
.
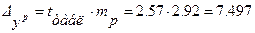Доверительный интервал прогнозируемого расхода составит:
,
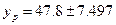т.е. при среднемесячной заработной плате, равной 8 тыс. руб., расходы на покупку продовольственных товаров составят не меньше чем
% - х пункта
и не больше чем
% - х пункта.
9. Рассчитайте средний коэффициент эластичности.
Средний коэффициент эластичности для линейной регрессии рассчитывается по формуле:
.
Таким образом, получаем, что с ростом среднемесячной заработной платы на 1 % расходы на покупку продовольственных товаров снижаются на 4,14 %.
10. Определить среднюю ошибку аппроксимации.
Средняя ошибка аппроксимации находится как средняя арифметическая простая из индивидуальных ошибок:
,
(см. последнюю графу расчетной таблицы 1).
Ошибка аппроксимации показывает хорошее соответствие расчетных и фактических данных: среднее отклонение составляет 2,98 %.
|
|
|
