 |
Бинарным отношением между Х и У называется любое подмножество прямого произведения
|
|
|
|
Прямое произведение
Прямым произведением множеств Х и У называется множества пар вида (х,у) таких, что х принадл Х, у принадл У.
Бинарным отношением между Х и У называется любое подмножество прямого произведения
Пусть f – отображение множества X в множество Y, g – отображение множества Y в множество Z. Композицией отображений f и g называется отображение
h = g o f, (1)
которое сопоставляет любому элементу a множества A элемент
h (a) = g (f (a)) (2)
множества C по правилу gof(x) = g(f(x)). Обратим внимание, что в обозначении операции композиции (1) первое выполняемое отображение пишется справа, второе – слева, что связано с записью (2).
Тождественное отображение
Это такое отображение множества Х самое в себя, такое что f(х) = х для любого х из Х
Обратное отображением
Пусть f – отображение из Х в У, а g – отображение из Y в X. Если fog явл. Тождественным отображением из Y в Y, то g называется правым обратным отображением
Пусть f – отображение из Х в У, а g – отображение из Y в X. Если gof явл. Тождественным отображением из X в X, то g называется левым братным отображением
если f является одновременно правым и левых обратным, то f называется обратным отображением
Отображение f имеет обратное тогда и только тогда, когда оно — биективно
Бинарное отношением ~ на Х называется отношением эквивалентности, если для люблых х, х' и x''
из Х Выполняются
1.х~x рефлективность
2.x~x'->x'~x симметричность
3.x~x', x'~x''->x~x'' транзитивность
Классом эквивалентности 
элемента 
называется подмножество элементов, эквивалентных . Из вышеприведённого определения немедленно следует, что, если 
, то 
.
Множество всех классов эквивалентности обозначается 
.
|
|
|
·Для класса эквивалентности элемента используются следующие обозначения: 
, 
, 
.
·Множество классов эквивалентности по отношению 
является разбиением множества.
Самое наглядное и всем знакомое отношение эквивалентности - разделение контингента учащихся конкретной школы на классы.
·Равенство («
»), тривиальное отношение эквивалентности на любом множестве, в частности, вещественных чисел.
·Сравнение по модулю, («а ≡ b (mod n)»).
Пусть на множестве 
задано отношение эквивалентности . Тогда множество всех классов эквивалентности называется фактор-множеством и обозначается 
. Разбиение множества на классы эквивалентных элементов называется его факторизацией.
Определение. Пусть А - произвольное множество, 
- его декартов квадрат. Внутренней бинарной алгебраической операцией намножестве А называют отображение 
.
Пусть А - произвольное множество. Для того, чтобы задать на множествеА алгебраическую операцию * необходимо выполнить два условия:
1) нужно определить правило, по которому любым двум элементам х и у множества А ставился бы в соответствие единственный для этой пары элементов (именно в этом порядке: х, у) элемент 
;
2) этот элемент должен принадлежать множеству А. В этом случае говорят, что множество А замкнуто относительно данной операции *.
Определение. Алгебраическая операция *, определенная на множестве А называется ассоциативной, если она подчиняется закону ассоциативности, т.е. для любых трех элементов х, у, z множества А выполняется равенство: 
.
Определение. Алгебраическая операция *, определенная на множестве А называется коммутативной, если она подчиняется закону коммутативности, т.е. для любых двух элементов х и у множества А выполняется равенство: х*у = у*х.
Тетрадь!!! 4 и 5 вопрос
Множество Х, с заданной на нем бинарной операцией называется группой, если выполняются след. Условия
|
|
|
1.бинарная операция ассоциативна
2.существует нейтральный(единичный элемент)
3.для каждого элемента х из Х существует обратный(x в -1)
Группа, обладающая коммутативностью называется абелевой.
Непустое множество 
с заданной на нём бинарной операцией 
называется группой , если выполнены следующие аксиомы:
1.ассоциативность: 
;
2. наличие нейтрального элемента: 
;
3. наличие обратного элемента: 
Целые числа с операцией сложения. группа с нейтральным элементом 0. Она является абелевой.
· Положительные рациональные числа с операцией умножения. Произведение рациональных чисел — снова рациональное число, обратный элемент к рациональному числу представляется обратной дробью, имеется ассоциативность и единица.
Симметрическая группа. Множество всех биекций конечного множества в себя с операцией композиции является конечной группой, которая называется симметрической группой, или группой перестановок. Любая конечная группа является подгруппой некоторой симметрической группы (теорема Кэли).
Симметрической группой множества X называется группа всех перестановок X (то есть биекций X → X) относительно операции композиции.
Симметрическая группа множества X обычно обозначается S (X). Если X = {1, 2,…, n }, то S (X) также обозначается через Sn.
Нейтральным элементом в симметрической группе является тождественная перестановка 
, определяемая кактождественное отображение:
для всех x из X.
В теории групп под перестановкой произвольного множества подразумевается биекция этого множества на себя. Как синоним слову "перестановка" в этом смысле некоторые авторы используют слово подстановка. (Другие авторы подстановкой называют наглядный способ записи перестановки.)
Число всех перестановок порядка 
равно числу размещений из n по n, то есть факториалу
Перестановку также можно записать в виде произведения непересекающихся циклов, причём единственным образом с точностью до порядка следования циклов в произведении. Например:
Определение А. 16. Циклом или n-цикломназывается перестановка ƒ, действующая по правилу:
и ƒ(x) = х, если х
Например, перестановка
|
|
|
является циклом, который можно записать по-разному: (1,2,3) = = (2,3,1) = (3,1,2).
Лемма А, 17, Любую перестановку можно представить в виде произведения независимых циклов. Доказательство, ПустьОбозначим черезцикл
в котором мы применяем а до тех пор, пока не получим снова 1. Затем берем такое число х{1,..., n}, что (х) = x, и определяем второй цикл
После этого возьмем число, которое остается неподвижным как при действии, так и, и определяем цикл. Будем продолжать процесс до тех пор, пока не исчерпаем все натуральные числа от 1 до n. Полученные в результате циклы,...,, очевидно, независимы, а их произведение равно исходной перестановке.
Очень приятно, что приведенное доказательство конструктивно, в том смысле, что дает алгоритм разложения произвольной перестановки в произведение независимых циклов. Разберем пример, взяв в качествеперестановку
Тогда (1) = 2, (2) = 3, (3) = 7 и (7) = 1. Получили первый цикл:
= (1,2,3,7).
Следующий элемент, который мы должны рассмотреть — это 4, поскольку это минимальный элемент множества {1,..., 9}, который неподвижен при действии (4) = 6,(6) = 4. Поэтому = (4, 6).
Продолжая процесс, получаем = (5,8) и = (9), Следовательно,
= (1,2,3,7)(4,6)(5,8)(9) = (1,2,3,7)(4,б)(5,8).
Кольцо — это множество R, на котором заданы две бинарные операции: + и × (называемые сложение и умножение), со следующими свойствами:
1. 
— коммутативность сложения;
2. 
— ассоциативность сложения;
3. 
— существование нейтрального элемента относительно сложения;
4. — существование противоположного элемента относительно сложения;
5. 
— ассоциативность умножения (некоторые авторы не требуют выполнения этой аксиомы[1])
6. 
— дистрибутивность.
Ассоциативные кольца могут обладать следующими дополнительными свойствами:
·наличие единицы: (кольцо с единицей);
·коммутативность умножения: 
(коммутативное кольцо);
·отсутствие делителей нуля: 
(целостное кольцо или область целостности).
Пусть 
— кольцо, тогда выполнены следующие свойства:
· 
, то есть 0 — поглощающий элемент по умножению.
· 
, где 
— элемент, обратный к 
по сложению.
|
|
|
·
· 
— целые числа (с обычным сложением и умножением). Это важнейший пример кольца, так как любое кольцо можно рассматривать как алгебру над 
.
· 
— кольцо вычетов по модулю натурального числа n. Это классические примеры колец из теории чисел. Они являются полями тогда и только тогда, когда число 
простое. Соответствующие поля являются отправной точкой для построения теории конечных полей. Кольца вычетов также важны при исследовании структуры конечнопорождённых абелевых групп, Их также можно использовать для построения p-адических чисел.
· 
— кольцо рациональных чисел, являющееся полем. Это простейшее поле характеристики 0. Оно является основным объектом исследования в теории чисел. Пополнение его по всем неэквивалентным нормам даёт поля вещественных чисел 
и p-адических чисел 
, где 
— произвольное простое число.
По́лем называется множество F с двумя бинарными операциями 
(аддитивная операция, или сложение) и 
(мультипликативная операция, или умножение), если оно (вместе с этими операциями) образует коммутативное ассоциативное кольцо c единицей 
, все ненулевые элементы которого обратимы.
Иными словами, множество F с двумя бинарными операциями (сложение) и (умножение) называется полем, если оно образует коммутативную группу по сложению 
, все его ненулевые элементы образуют коммутативную группу по умножению 
, и выполняется свойство дистрибутивности.
— рациональные числа,
· 
— вещественные числа,
· 
— комплексные числа,
· 
— поле вычетов по модулю , где — простое число.
Элемент С из поля К называется корнем или нулем многочлена, если f(c) = 0
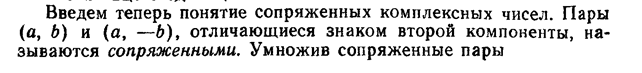
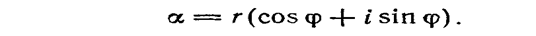
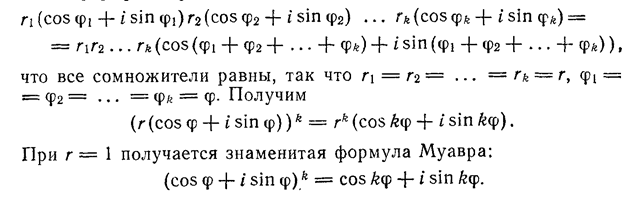
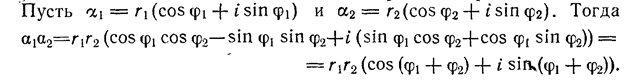
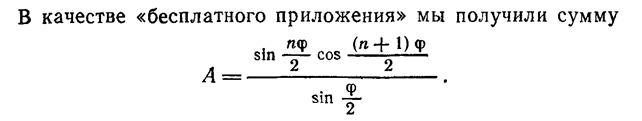
В абстрактной алгебре ненулевой элемент a кольца называется левым делителем нуля, если существует ненулевое b такое, что ab = 0.
Аналогично, ненулевой элемент a кольца является правым делителем нуля, если существует ненулевое b такое, что ba = 0.
Элемент, который одновременно является и правым, и левым делителем нуля, называется делителем нуля. Если умножение в кольце коммутативно, то понятия правого и левого делителя совпадают. Ненулевой элемент кольца, который не являются ни правым, ни левым делителем нуля, называется обычным элементом.
Пример: в кольце 
элементы 2, 3, 4 — делители нуля.
Ассоциативное коммутативное кольцо без делителей нуля называется областью целостности.
|
|
|
Обратимым элементом, а также единицей кольца или делителем единицы, называется всякий элемент 
кольца, для которого существует обратный элемент относительно умножения, то есть такой элемент , что 
, где e — единичный элемент кольца.
Множество всех обратимых элементов кольца образует мультипликативную группу, называемую группой единиц или группой обратимых элементов.
Если — делитель единицы, то элементы 
и называются ассоциированными с 
.
Обычно понятия делителя единицы и ассоциированного элемента употребляются для областей целостности.
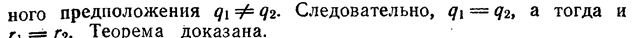
Область целостности (или целостное кольцо, или область цельности или просто область) — понятие абстрактной алгебры: ассоциативное коммутативное кольцо без делителя нуля (произведение ненулевых элементов не равно 0).
Евклидово кольцо — это область целостности R, для которой определена евклидова функция (евклидова норма) 
, причём , и возможно деление с остатком, по норме меньшим делителя, то есть для любых 
имеется представление 
, для которого 
.
Кольцо целых чисел . Пример евклидовой функции — абсолютная величина 
.
·Кольцо целых гауссовых чисел 
(где i — мнимая единица, 
) с нормой 
— евклидово.
·Произвольное поле 
является евклидовым кольцом с нормой, равной 1 для всех элементов, кроме 0.
·Кольцо многочленов в одной переменной 
над полем . Пример евклидовой функции — степень deg.
В евклидовом кольце осуществим алгоритм Евклида нахождения наибольшего общего делителя двух чисел (элементов). Пусть изначально даны два элемента a0 и a1, причём 
и 
. Деление с остатком даёт элемент 
с 
. Если он не равен нулю, можно опять применить деление с остатком, и получить элемент 
, и т. д. Таким образом генерируется цепочка значений 
с 
. Однако эта цепочка прерывается, поскольку всякое число из 
может строго превосходить лишь конечное количество других таких чисел. Это означает, что при некотором n остаток an+1 равен нулю, а an не равен, он и есть НОД элементов a0 и a1. Следовательно, в евклидовом кольце гарантировано завершение алгоритма Евклида. Строго говоря, именно в евклидовых кольцах и возможна реализация алгоритма Евклида.
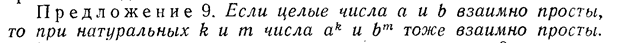
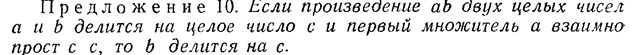
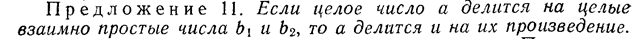
Изоморфизм
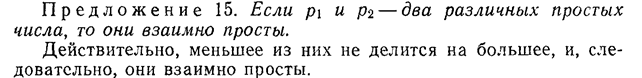
Теоре́ма Э́йлера в теории чисел гласит:
Если и  взаимно просты, то  , где  — функция Эйлера.
|
Функция Эйлера φ(n) — мультипликативная арифметическая функция, равная количеству натуральных чисел, меньших n и взаимно простых с ним. При этом полагают, что число 1 взаимно просто со всеми натуральными числами, и φ(1) = 1.[1]
Общий вид линейного диофантова уравнения:
В частности, линейное диофантово уравнение с двумя неизвестными имеет вид:
Если 
(то есть 
не делится нацело на наибольший общий делитель 
), то уравнение (1) не разрешимо в целых числах. В самом деле, если , то число, стоящее слева в (1), делится на , а стоящее справа — нет. Справедливо и обратное: если в уравнении выполняется 
, то оно разрешимо в целых числах.
Пусть 
— частное решение уравнения . Тогда все его решения находятся по формулам:
Доказательство. То, что правые части указанных в формулировке теоремы равенств действительно являются решениями, проверяется их непосредственной подстановкой в исходное уравнение. Покажем, что любое решение уравнения ax + by = c имеет именно такой вид, какой указан в формулировке теоремы. Пусть { x *, y *} - какое-нибудь решение уравнения ax + by = c. Тогда ax * + by * = c, но ведь и ax 0 + by 0 = c. Следуя многолетней традиции доказательства подобных теорем, вычтем из первого равенства второе и получим:
a (x *- x 0) + b (y *- y 0) = 0
- однородное уравнение. Далее, глядя на случай 1, рассмотрение которого завершилось несколькими строками выше, пишем сразу общее решение: x *- x 0 = - bt, y *- y 0 = at, откуда моментально, используя навыки третьего класса средней школы, получаем:
| ì í î | x * = x 0- bt, y * = y 0 + at. |
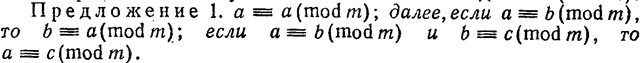
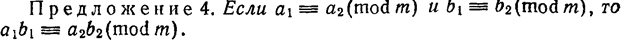
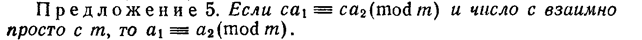
Если натуральные числа 
попарно взаимно просты, то для любых целых 
таких, что 
при всех 
, найдётся число 
, которое при делении на 
даёт остаток 
при всех . Более того, если найдутся два таких числа 
и 
, то .
|
|
|
