 |
Метод математической индукции по n
|
|
|
|
Воспользуемся методом математической индукции. При 
утверждение теоремы очевидно. Пусть теорема справедлива при 
, т. е. существует число 
, дающее остаток 
при делении на 
при 
. Обозначим
и рассмотрим числа 
. Покажем, что хотя бы одно из этих чисел даёт остаток 
при делении на 
. Допустим это не так. Поскольку количество чисел равно , а возможных остатков при делении этих чисел на может быть не более чем (ведь ни одно число не даёт остаток 
), то среди них найдутся два числа, имеющих равные остатки (принцип ящиков Дирихле). Пусть это числа 
и 
при 
, 
и . Тогда их разность делится на , что невозможно, т. к. 
и 
взаимно просто с , ибо числа 
попарно взаимно просты (по условию). Противоречие.
Таким образом, среди рассматриваемых чисел найдётся число 
, которое при делении на даёт остаток . В то же время при делении на 
число даёт остатки 
соответственно.
Докажем теперь, что 
. В самом деле 
, то есть 
. Так как все взаимно просты, то 
делится на их произведение. ■
Неприводимый многочлен над полем 
― многочлен 
от 
переменных над полем является простым элементом кольца 
, то есть, непредставим в виде произведения 
, где 
и 
― многочлены с коэффициентами из , отличные от констант.
Многочлен называется абсолютно неприводимым, если он неприводим над алгебраическим замыканием поля коэффициентов. Абсолютно неприводимые многочлены одной переменной ― это многочлены 1-й степени и только они. В случае нескольких переменных существуют абсолютно неприводимые многочлены сколь угодно высокой степени — например, любой многочлен вида
абсолютно неприводим.
Корни неприводимого многочлена называются сопряженными.
|
|
|
Для произвольного не равного тождественно постоянной многочлена 
с комплексными коэффициентами множество нулей его производной 
принадлежитвыпуклой оболочке нулей многочлена .
!!!!!!!!!!!!!!!!!!!!!!
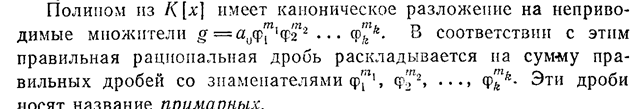
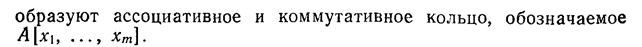
Симметри́ческий многочле́н — многочлен от n переменных 
, не изменяющийся при всех перестановках входящих в него переменных.
Билет 43.
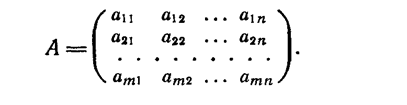
Билет 44
Билет 45
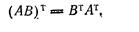
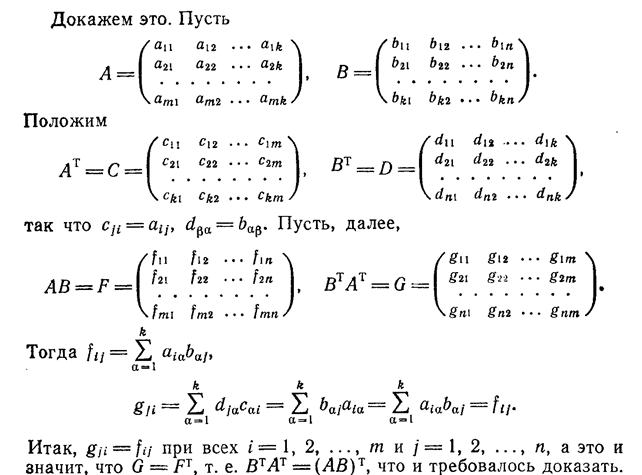
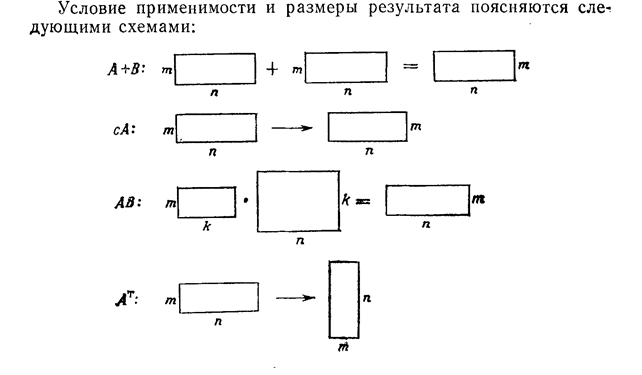
Билет 46
Билет 47
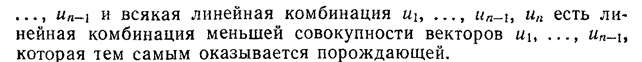
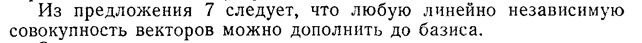
число векторов, сост. Базис, называется размерностью пространства.
Читать страница 306
Элементарными преобразованиями строк называют:
·перестановка местами любых двух строк матрицы;
·умножение любой строки матрицы на константу , 
;
·прибавление к любой строке матрицы другой строки.
Единичная — на диагонали все 1.
матрицы
http://mathhelpplanet.com/static.php?p=elementarnye-pryeobrazovaniya-kak-umnozheniya-matrits
Ступенчатая матрица — матрица, имеющая m строк, у которой первые r диагональных элементов ненулевые, r ≤ m, а элементы, лежащие ниже диагонали и элементы последних m − r строк равны нулю:
1: Если в совместной системе все переменные главные, то такая система является определённой.
2: Если количество переменных в системе превосходит число уравнений, то такая система является либо неопределённой, либо несовместной.
54
PDQ
Пусть 
— прямоугольная матрица.
Тогда по определению рангом матрицы 
является:
·нуль, если — нулевая матрица;
·число 
, где 
— минор матрицы порядка , а 
— окаймляющий к нему минор порядка 
, если они существуют.
|
|
|
Теорема (о корректности определения рангов). Пусть все миноры матрицы порядка равны нулю ( ). Тогда  , если они существуют.
|
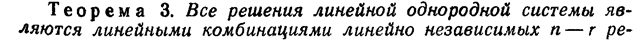
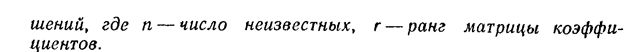
Теорема Кронекера-Капелли
Для того чтобы линейная система являлась совместной, необходимо и достаточно, что бы ранг расширенной матрицы этой системы был равен рангу ее основной матрицы.
Необходимость
Пусть система совместна. Тогда существуют числа 
такие, что 
. Следовательно, столбец 
является линейной комбинацией столбцов 
матрицы . Из того, что ранг матрицы не изменится, если из системы его строк (столбцов) вычеркнуть или приписать строку (столбец), которая является линейной комбинацией других строк (столбцов) следует, что .
[править]Достаточность
Пусть 
. Возьмем в матрице какой-нибудь базисный минор. Так как 
, то он же и будет базисным минором и матрицы 
. Тогда согласно теореме о базисном миноре последний столбец матрицы будет линейной комбинацией базисных столбцов, то есть столбцов матрицы . Следовательно, столбец свободных членов системы является линейной комбинацией столбцов матрицы .
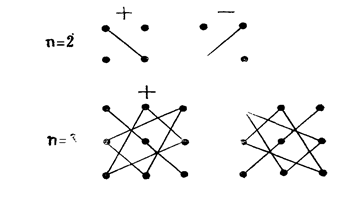
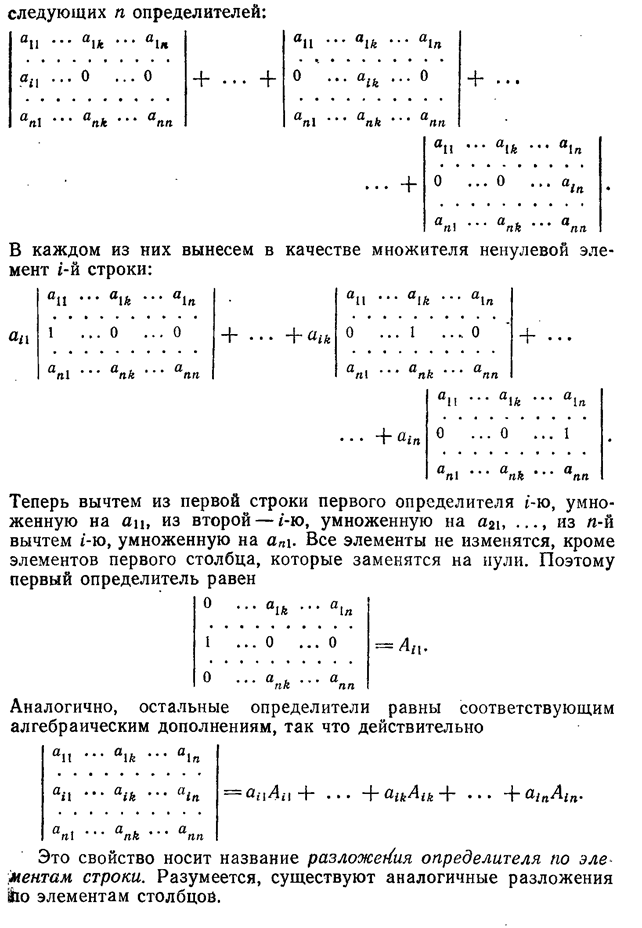
| A⋅B |=| A |⋅| B |.
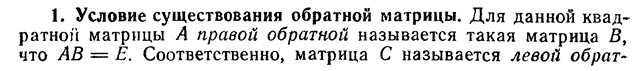
Билет 46
Свойства нуля и обратного элемента
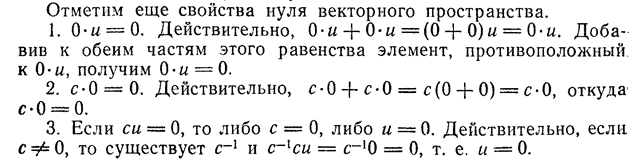
Линейная оболочка
Пусть u1,u2 … un – элементы линейного пространства
а с1,с2... сn принадлежат К.
Тогда с1 * u1+c2 * u2...cn * un называется линейной комбинацией.
Совокупность всех линейных комбинаций называется линейной оболочкой этих элементов и обозначается <u1, u2... un>
Очевидно, что линейная оболочка является подпространством основного линейного пространства.
Векторные поля и линейные операторы. Жорданова форма. Последние вопросы
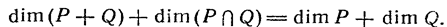
критерий прямой суммы — в тетради!!
|
|
|
