Главная | Обратная связь | Поможем написать вашу работу!

Краткие теоретические сведения.

Теплоемкость тела характеризуется количеством теплоты, необходимым для нагревание этого тела на один градус (Дж/град). Если для увеличения температуры тела на Т градусов необходимо сообщить ему ΔQ джоулей, то средняя теплоемкость тела в интервале ΔТ определяется как:

(1)

Теплоемкость тела пропорциональна массе и зависит от вещества тела. Удельная теплоемкость С_уд данного вещества (дерева, железа, воздуха и т. д.) характеризуется количеством тепла на один градус, и измеряется в Дж/кг град. Удельная теплоемкость.

Для газов удобно пользоваться молярной теплоемкостью (С_мол или просто С), характеризующейся количеством теплоты, нужным для нагревания одного киломоля данного вещества на один градус.

Очевидно, что

С_уд/Дж/кг_*град/_*μ/кг/кмоль/ = С /Дж/кмоль_*град/.

Поскольку в 1 киломоле любого газа содержится одинаковое количество молекул, а средняя кинетическая энергия молекул не зависит от их массы, то можно ожидать, что молярные теплоемкости всех достаточно разреженных газов должны быть одинаковыми.

Теплоемкость тела существенно зависит от того, как меняются состояния тела в процессе нагревания. Рассмотрим для простоты идеальный одноатомный газ. Если мы будем нагревать газ, заключенный в замкнутом объеме, V = const (рис. 1, а), то все подводимое тепло ΔQ будет идти только на увеличение внутренней энергии газа. Тогда первое начало термодинамики при ΔA = 0 будет иметь вид: ΔQ = ΔU.

При этом температура газа будет возрастать в соответствии с увеличением его внутренней энергии, откуда следует, что температура идеального газа пропорциональна его внутренней энергии. Давление газа Р. также будет возрастать пропорционально температуре. Обозначим теплоемкость газа при постоянном объеме через С.

Если хотим, чтобы в процессе нагревания сохранилось давление, газу следует предоставить возможность расширяться. Для этого поместим газ в цилиндр с поршнем, на который действует постоянное давление Р. = const (рис. 1, б). Так как внутренняя энергия U идеального газа не зависит от его объема, то количество теплоты, необходимое для ее увеличения, останется тем же. Но при нагревании газа до той же температуры часть подводимого тепла расходуется теперь на работу против внешних сил при расширении газа. Следовательно, для нагревания газа до той же температуры, как и в предыдущем случае (V = const), придется затратить большее количество теплоты. Таким образом, теплоемкость ΔQ/ΔТ газа при постоянном давлении, которую мы обозначим через С_р., будет больше, чем С_V.

Рассмотренный пример очень важен. Он показывает, что количество теплоты ΔQ, необходимое для нагревания газа на ΔТ градусов, существенно зависит от дополнительных условий – характера измерений других микроскопических параметров, определяющих состояние газа, т. е. Р. и V. Кроме рассмотренных процессов, характеризуемых простейшими дополнительными условиями V = const и Р. = const, можно рассмотреть и множество других, отвечающих различным изменениям V и Р. при нагревании. Каждому процессу будет отвечать своя теплоемкость С.

Величины С_р. и С_v для идеального газа оказывается связанными простым соотношением:

С_р. – С_v= R (2)

Это соотношение носит название закона Роберта Майера, полученного им в 1842 году.

Для идеального газа молярная теплоемкость при постоянном давлении превышают молярную теплоемкость при постоянном объеме на величину R т. е. на 8,31 кДж/кмоль град.

Универсальная газовая постоянная R численно равна работе расширения киломоля идеального газа при нагревании его на один градус при постоянном давлении.

Опыт показывает, что во всех случаях превращение механической энергии в тепловую и обратно совершается всегда в строго эквивалентных количествах. Поскольку тепловое движение есть в конечном счете, тоже механическое движение отдельных молекул (только не направленное, а хаотическое), то при всех этих превращениях должен соблюдаться закон сохранения энергии с учетом энергии не только внешних, но и внутренних движений. Такая общая формулировка этого закона носит название первого начала термодинамики и записывается в виде:

ΔQ = ΔU + ΔA, т. е.

Количество теплоты, сообщенное телу (ΔQ), идет на увеличение внутренней энергии (ΔU) и на совершение теплом работы (ΔА).

Однако, если сосуд с расширяющим газом теплоизолировать от окружающей среды, то теплообмен будет отсутствовать, т. е. ΔQ = 0. Процесс, происходящий при таком условии, называется адиабатическим. Уравнение первого начала термодинамики для адиабатического процесса тогда примет вид:

ΔQ = 0 0 = ΔU + ΔA или ΔА = - ΔU. (3)

Следовательно, при адиабатическом процессе работа совершается только за счет внутренней энергии газа. При адиабатическом расширении газ совершает работу, а его внутренняя энергия и, следовательно, температура падают. При адиабатическом сжатии работа газа отрицательная (внешняя среда производит работу над газом), внутренняя энергия и температура газа возрастают.

Теплоемкость при адиабатическом процессе будет равна 0, т. е.

Уравнение, описывающее адиабатический процесс имеет вид:

PV^γ = const; где γ = С_Р/С_V. (4)

Рис.2

Так как С_Р>С_V, то γ>1 и кривая, изображаемая уравнением (4), идет круче изотермы (рис. 2). Величина работы адиабатического процесса может быть особенно просто вычислена с помощью уравнения (3):

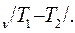
Для одноатомного газа С =12,5кДж/к моль град, С_р.=С_v+ =20,8 кДж/к моль град и показатель степени адиабаты γ=С_Р/С_v=1,67.

Для двухатомных газов при обычных температурах

g=29,1/20,8=1,4.

Для многоатомных газов γ еще ближе к единице.

В быстроходных двигателях внутреннего сгорания и при истечении газов через сопла реактивных двигателей процесс расширения газа протекает настолько быстро, что его можно считать практически адиабатическим и

рассчитывать по уравнению /4/.

Опыт также показывает, что для звуковых колебаний с минимальными частотами за время одного колебания /~0,1с/температура между сжатыми/ и тем самым разогретыми/ и разряженными /и тем самым охлажденными/ областями волны не успевает выравниваться. Практически процесс распространения звука можно считать адиабатическим, так что скорость распространения звука в идеальном газе определяется выражением:

где

Отсюда легко найти :

(5)

Таким образом, определение γ сводится к измерению скорости звука и абсолютной температуры воздуха. В данной работе скорость звука определяется методом стоячих волн - методом Кундта.

II. ОПИСАНИЕ ЭКСПЕРИМЕНТАЛЬНОЙ УСТАНОВКИ.

Схема экспериментальной установки изображена на рисунке 3. Телефон т, получая электрический сигнал от генератора1, излучает звуковые волны в трубу 2. Достигнув микрофона М, звуковая волна преобразуется в напряжение, которое поступает на вертикально отклоняющие пластины У электронного осциллографа 3.Напряжение на горизонтально отклоняющие пластины X подается непосредственно с выходных клемм звукового генератора. Телефон жестко закреплен на левом конце трубы, а микрофон может свободно перемещаться внутри нее.

Рис.3

Фазовый сдвиг сигнала, поступающего на пластины У, относительно сигнала, подведенного к пластинам X зависит от времени, которое тратит звук на прохождение расстояния между микрофоном и телефоном, может быть использована для определения длины волны λ. При включении установки на экране осциллографа должен быть виден эллис. Изменяя расстояние между микрофоном и телефоном, можно добиться превращения эллипса в прямую линию. Если теперь сместить микрофон на λ/2, то на экране вновь возникнет прямая линия, проходящая на этот раз через другие квадранты. При дальнейшем смещении прямая вновь переменит свое направление и т.д. Таким образом, при помощи фигур, получивших название фигур Лиссажу, можно непосредственно измерить длину звуковой волны в воздухе и по формуле определить скорость звука, где - частота генератора в Гц.

III.ПОРЯДОК ПРОВЕДЕНИЯ ИЗМЕРЕНИЙ.

1. Включите осциллограф и дайте ему прогреться в течение 10 минут.

2. Включите и настройте звуковой генератор на частоту /частота задается преподавателем/.Установите напряжение на выходе генератора 1,5 В.

3. Установите указатель штока микрофона 5 в крайнее правое положение шкалы 4 /рис/, при этом на экране осциллографа появится фигура Лиссажу /эллипс или прямая линия/.

4. Перемещая шток с микрофоном в лево, зафиксируйте положение штока микрофона / /, при которых эллипс превращается в четкую прямую линию, что соответствует узлам стоячей волны /отсчет производить в см по шкале 4/.

5. Вычислите разность между узловыми точками, которая является половиной длины волны .

6. Вычислите длину волны и скорость звуковой волны по формуле .

7. Определите термометром температуру окружающей среды.

8. Вычислите по формуле /5/.

9. Оцените погрешность измерений по формуле:

;

10. Результаты измерений занесите в таблицу:

Таблица 1

Результаты эксперимента


1.
2.
3.
Ср.

11.Сделайте выводы.

IV. КОНТРОЛЬНЫЕ ВОПРОСЫ.

Смотри работу №10.

ЛАБОРАТОРНАЯ РАБОТА № 11

ОПРЕДЕЛЕНИЕ СРЕДНЕЙ ДЛИНЫ СВОБОДНОГО ПРОБЕГА МОЛЕКУЛ ВОЗДУХА

ЦЕЛЬ РАБОТЫ: изучение основ молекулярно-кинетической теории газов и определение средней длины свободного пробега молекул воздуха.

ПРИБОРЫ И ПРИНАДЛЕЖНОСТИ: делительная воронка, мерный стакан, секундомер, термометр, барометр.

I.КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ.

Молекулярно- кинетическая теория строения вещества основана на трех положениях:

1. Все вещества состоят из отдельных частиц-молекул.

2. Между молекулами одновременно действуют силы взаимного притяжения и отталкивания.

3. Молекулы находятся в состоянии непрерывного беспорядочного движения.

В газах молекулы находятся на значительно большем расстоянии друг от друга, чем в жидкостях и твердых телах, и сила взаимного притяжения очень мала. Совершая хаотические движения, молекулы газа сталкиваются друг с другом, при этом изменяется их скорость движения, как по направлению, так и по величине.

Следует отметить, что молекулы сталкиваются друг с другом не соприкасаясь, т.к. уже при сближении в 10^-10м действуют значительные силы взаимного отталкивания.

То минимальное расстояние (между центрами молекул), на котором происходит столкновение, называется эффективным диаметром молекул. Путь, пройденный молекулой между двумя последовательными столкновениями, называется длиной свободного пробега молекул. Длина этого пути не одинакова, но благодаря большому числу молекул и беспорядочности их движения, можно говорить о средней длине свободного пробега молекул λ:

где -средняя скорость молекул,

u- число столкновений.

Средняя длина свободного пробега зависит от плотности, давления и температуры газа. С увеличением плотности и давления газа средняя длина свободного пробега уменьшится, а с повышением температуры она возрастет. Длина свободного пробега является важной характеристикой состояния газа.

В данной работе длина свободного пробега определяется из формулы, связывающей длину свободного пробега λ с коэффициентом внутреннего трения η:

где η -коэффициент внутреннего трения.

-плотность газа,

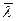-длина свободного пробега молекул,

-средняя арифметическая скорость молекул.

Из формулы (1) найдем:

Плотность газа можно найти из уравнения Менделеева-Клапейрона

откуда

где p-давление газа,

-молярная масса,

R -универсальная газовая постоянная,

T -температура.

Средняя арифметическая скорость, согласно молекулярно-кинетической теории, равна:

(4)

Коэффициент внутреннего трения найдем из формулы Пуазейля:

(5)

где r – радиус трубки, по которой течет газ,

l – длина трубки,

V – объем протекшего газа,

t - время течения данного объема газа по трубке,

р – разность давлений на концах трубки.

Подставляя (3,4,5) в формулу (2) получим:

(6)

После преобразований формула (6) примет вид:

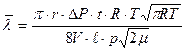(7)

Эта формула (7) и является расчетной для определения средней длины свободного пробега молекул газа.

II. ОПИСАНИЕ ЭКСПЕРИМЕНТА УСТАНОВКИ

Рис.1

Лабораторная установка представляет собой делительную воронку А (рис.1), укрепленную на штативе. На воронку нанесена миллиметровая шкала В, на которой отмечается уровень воды в воронке. В воронку заливается дистиллированная вода на ¾ сосуда и закрывается пробкой, в которую вставлен капилляр L. Если открыть кран делительной воронки К, то вода будет выдавливаться под действием силы тяжести. Давление воздуха в сосуде станет меньше атмосферного и вода начнет вытекать не непрерывной струей, а отдельными порциями. Скорость вытекания воды сильно зависит от радиуса r. На концах капилляра создается разность давления р., численно равная гидростатическому давлению столба жидкости в воронке:

где 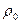- плотность воды, g – ускорение силы тяжести, h_ср – средний уровень воды в воронке.

Разность давления будет заставлять воздух втекать в сосуд через капилляр. Через некоторый промежуток времени установится равномерное течение воздуха в капилляре, при котором объем воздуха, вошедшего через капилляр в воронку, будет равен объему вытекшей из воронки воды.

III. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

1. Залейте в делительную воронку, дистиллированную воду и плотно закройте пробкой с капилляром.

2. Подставьте под кран воронки химический стакан. Откройте кран и, когда вода начнет вытекать отдельными порциями, подставьте мерный стакан. Отметьте уровень воды в воронке h ₁ и включите секундомер.

3. Наберите в мерный стакан определенное количество воды (объем воды задается преподавателем), остановите секундомер и запишите время t, в течении которого вытекала вода, а, следовательно, и втекал воздух.

4. Отметьте уровень воды в воронке h₂.

5. Вычислите разность давлений по формуле:

принимая ₀ = 1000 г/м³, а g = 981 м/с².

( - есть средний уровень воды в воронке).

6. Снимите показания барометра и термометра, учитывая, что Т = t + 273 и

1 мм рт.ст. = 1333 дин/см².

7. Выпишите табличные данные для R = 8,31*10⁷ эрг/К моль

= 3,14; m = 0,029 г/моль

8.Вычислите длину свободного пробега молекул воздуха по формуле (7)

9. Данные измерения занесите в таблицу 1 и 2.

Таблица 1

Постоянные величины

	m, г/моль	R,	r, см	l, см	V, см³	g, см/с²

Таблица 2

Результаты эксперимента

№:	h, cм	h₂, см	р., дин/см²	t, с	Т,К	Р., дин/см²	, см
1. 2. 3.
Ср.

10. Сделайте выводы.

IV. КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Что такое скорость поступательного движения молекул газа?

2. Что принимается под средней длиной свободного пробега молекул? От каких характеристик состояния газа она зависит?

3. Объясните механизм взаимодействия молекул при столкновениях. Что называется эффективным диаметром молекул газа?

ЛАБОРАТОРНАЯ РАБОТА № 12

ОПРЕДЕЛЕНИЕ ПРИРАЩЕНИЯ ЭНТРОПИИ ПРИ ПЛАВЛЕНИИ ТВЕРДОГО ТЕЛА

ЦЕЛЬ РАБОТЫ: изучение второго начала термодинамики и определение изменения энтропии при плавлении нафталина.

ПРИБОРЫ И ПРИНАДЛЕЖНОСТИ: пробирка с нафталином, термометр, электроплитка, стакан с водой, штатив с держателем.

1. КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ.

Закон сохранения энергии устанавливает взаимопревращаемость различных видов энергии, но не указывает направленность этих процессов. Все виды энергии можно перевести в теплоту, однако теплота может быть превращена в другие виды энергии только с помощью специальных машин. При этом часть теплоты обязательно теряется, т.е. невозможен механизм, который все получаемое от нагревателя количество теплоты целиком переводил бы работе, часть этого количества теплоты должна быть отдана холодильнику. Это одна из формулировок второго начала термодинамики.

Коэффициент полезного действия (кпд) тепловой машины определяется выражением:

= где

Т₁ – температура нагревателя;

Т₂– температура холодильника

Отсюда видно, что коэффициент полезного действия тепловой машины тем больше, чем больше разность температур нагревателя и холодильника. Практически невозможно превратить в работу огромное количество тепла, содержащееся в воде морей и океанов, так как разность температуры окружающих тел и воды незначительна.

Для оценки «качества» теплоты в этом отношении, а также для количественного учета обесценивания и рассеивания теплоты в термодинамике пользуются величиной, которая называется приведенной теплотой:

Q_пр= ,

Т.е. это количество теплоты, приходящееся на один градус Кельвина.

Важной характеристикой является изменение приведенной теплоты при различных процессах. Если приведенная теплота возрастает, это значит, что возможности полезного использования теплоты уменьшилось и наоборот.

Однако в термодинамике чаше пользуются величиной, получившей название энтропии S, которая выражается через приведенные теплоты:

т.е. разбивают весь процесс на достаточно малые участки и суммируют, считая, что температура в пределах каждого из этих участков постоянная. Тогда S ₁ и S ₂ – энтропия в начальном и конечном состояниях системы, а - теплоты, сообщаемое или отнимаемое от системы на элементарном участке.

Другая формулировка второго начала термодинамики следующая: энтропия термодинамических систем однозначная функция состояния этих систем.

Функцией состояния называется такая физическая характеристика системы, изменение которой при переходе системы из одного состояния в другое не зависит от вида соответствующего этому переходу термодинамического процесса, а целиком определяется значениями параметров начального и конечного состояний.

Важнейшими функциями состояния системы являются внутренняя энергия U, энтропия S и свободная энергия F = U – T* S, где T* S – это часть внутренней энергии, которая не может быть превращена в теплоту и называется связанной энергией.

Изменение энтропии можно подсчитать по следующей формуле:

(1)

По закону изменения энтропии системы в обратном процессе можно судить о направлении теплообмена (при нагревании тела возрастает, при охлаждении – убывает). При равновесных адиабатических процессах dQ = 0 и S не изменяется. При других процессах – изохорическом, изобарическом и изотермическом энтропии изменяется.

Так для изотермического процесса (Т = const):

В неизолированных системах S всегда возрастает, и уравнение будет иметь вид:

Знак равенства относится к обратимым процессам (т.е. процессам, которые можно провести в обратном направлении через те же самые состояния), а знак неравенства – к необратимым. Все реальные процессы – необратимы.

Между энтропией и вероятностью состояния существует связь. Больцман установил ее в виде соотношения:

S = k*ln*

где k – постоянная Больцмана,

- число различных способов, которыми может быть реализовано определенное состояние, называемое термодинамической вероятностью.

В соответствии с формулой Больцмана второе начало термодинамики можно сформулировать следующим образом: «Во всякой изолированной системе происходит такие изменения, которые приводят систему к наиболее вероятному состоянию».

II. ОПИСАНИЕ ЭКСПЕРИМЕНТАЛЬНОЙ УСТАНОВКИ.

В данной работе рассматривается изменение энтропии при нагревании и плавлении нафталина. Так как нафталин является кристаллическим веществом, то он плавится при определенной температуре.

Количество теплоты, которое надо затратить, чтобы нагреть нафталин от комнатной температуры Т_к до температуры плавления Т_попределяется по формуле:

С*m*d*T,

где С – удельная теплоемкость нафталина (1222 Дж/кг*К)

m - масса нафталина.

Количество теплоты, необходимое для плавления нафталина при температуре плавления (Т_п=const), равно:

Q₂ = *m, где

- удельная теплота плавления нафталина (2*10⁵ Дж/кг).

Тогда приращение энтропии при плавлении нафталина можно подсчитать по формуле (1), подставив вместо Q его значение Q₁ + Q₂. Тогда получим:

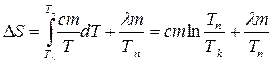(2)

Рис.1

Экспериментальная установка для определения (рис.1) состоит из пробирки нафталином 1, в которую помещен термометр 2. Пробирка опускается в стакан с водой 3, который ставится на электрическую плитку 4.

III. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ.

1. Соберите установку по схеме (рис. 1)

2. Включите плитку в сеть и следите за изменением температуры в пробирке.

3. Как только температура нафталина станет выше комнатной, снимите показания термометра через каждые 15 секунд до температуры нафталина 95-100⁰С.

4. Выключите плитку из сети и освободите пробирку нафталином от сосуда с водой.

5. Снимите показания термометра через каждые 15 секунд в обратном порядке (при охлаждении нафталина).

6. Результаты измерений занесите в таблицу 1:

Таблица 1

№ п/п	Время нагревания, с	Температура
t, ⁰С	Т, К

7. Постройте график зависимости температуры нафталина от времени его нагрева и охлаждения и сделайте выводы.

8. Вычислите по формуле (2) приращение энтропии при нагревании и плавлении нафталина.

9. Сделайте выводы.

IV. КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Какие процессы называются обратимыми и необратимыми? Приведите примеры.

2. Сформулируйте второе начало термодинамики.

3. Поясните работу тепловой машины, работающей по циклу Карно. Каков кпд тепловой машины?

4. Дайте понятие энтропии.

ЛАБОРАТОРНАЯ РАБОТА № 13

ОПРЕДЕЛЕНИЕ СОПРОТИВЛЕНИЯ ПРОВОДНИКОВ МОСТИКОМ УИТСТОНА

ЦЕЛЬ РАБОТЫ:изучить методы расчета электрических цепей, и определить сопротивление проводников мостиком Уитстона.

ПРИБОРЫ И ПРИНАДЛЕЖНОСТИ: реохорд, набор сопротивлений, магазин сопротивлений, гальванометр, ключ, источник постоянного тока.

I. Краткие теоретические сведения.

По своим электрическим свойствам все тела делятся на три класса: проводники, полупроводники и диэлектрики.

Те тела, в которых электрический заряд может свободно перемещаться по всему телу, называется проводниками электричества. Тела, в которых заряды не могут перемещаться из одной части в другую, называются изоляторами или диэлектриками.

Проводниками являются все металлы, а также электролиты и ионизированные газы. Такие вещества, как слюда, стекло, эбонит, фарфор, чистая вода являются диэлектриками.

Промежуточное положение занимают полупроводники, в которых перемещение зарядов в сильной степени зависит от внешних условий (особенно от температуры и от наличия в них примесей). К полупроводникам относятся сурьма, германий, кремний и др.

Проводники бывают двух родов. К проводникам первого рода относятся все металлы. Перемещающимися в них зарядами являются свободные электроны. При перемещении в них электронов в металле не происходит химических изменений.

К проводникам второго рода относятся растворы солей, кислот, щелочей. В них под действием электрического поля происходит перемещение положительных и отрицательных ионов. При этом в растворе и на электродах происходят химические превращения.

Упорядоченное движение зарядов называется электрическим током. За направление электрического тока условно принято направление движения положительного заряда. Количественной характеристикой электрического тока является скалярная величина, численно равна количеству электричества, проходящему через сечение проводника в единицу времени. Эта величина называется силой тока I. Единицей измерения силы тока в системе СИ является ампер (А).

Электрический ток, сила и направление которого не меняется с течением времени, называется постоянным. Если же сила и направление тока меняется – ток называется переменным. Для того, чтобы по проводнику аб (рис. 1) протекал постоянный электрический ток, необходимо создать на его концах постоянную разность потенциалов

Эта разность потенциалов называется напряжением и обозначается буквой U:

Единицей измерения напряжения в системе СИ служит вольт. Немецкий физик Ом установил, что сила тока в проводнике прямо пропорциональна напряжению на концах этого проводника:

где к – коэффициент пропорциональности, называемый проводимостью.

Величина, обратная проводимости, называется сопротивлением.

В системе СИ сопротивление измеряется в Омах.

Учитывая /2/, формула /1/ имеет вид:

Это соотношение выражает закон Ома для участка цепи: сила тока в проводнике прямо пропорциональна напряжению и обратно пропорциональна сопротивлению.

Сопротивление металлического проводника зависит от его размеров и свойств металла, из которого изготовлен проводник:

, где

ℓ -длина проводника,

S -площадь его сопротивления,

ρ -удельное сопротивление, т.е. сопротивление проводника длиной 1 м и площадью поперечного сечения 1 м² /система СИ/.

Удельное сопротивление является важной характеристикой металла. В системе СИ оно измеряется в Ом м.

С повышением температуры металла усиливается интенсивность хаотического движения электронов и колебательного движения ионов металлической решетки, что приводит к увеличению сопротивления проводника. Зависимость сопротивления проводника от температуры выражается формулой:

, где

R₀ -сопротивление проводника при 0⁰С,

ά -температурный коэффициент сопротивления.

Для поддержания постоянного тока в цепи необходимо поддерживать постоянное напряжение на ее концах. Для этого служит источник тока, внутри

которого происходит разделение положительных и отрицательных зарядов и перенос их на полюса источника тока. Силы, разделяющие заряды, имеют неэлектрическую природу и называются сторонними электроразделительными силами.

Работа, совершаемая сторонними силами по перемещению единичного положительного заряда внутри источника между его полюсами, называется электродвижущей силой (эдс).

В системе СИ эдс измеряется в Вольтах.

Если внешняя цепь разомкнута, то эдс равна разности потенциалов, возникающей на полюсах источника тока.

Всякая замкнутая цепь состоит из источника тока и нагрузки. Для замкнутой цепи закон Ома имеет вид:

, (6)

где R – внешнее сопротивление (т.е. сопротивление нагрузки, включая и сопротивление соединительных проводов).

r – внутреннее сопротивление (т.е. сопротивление самого источника тока).

Любая реальная электрическая цепь содержит несколько сопротивлений, соединенных между собой различными способами. Наиболее простые виды соединений это последовательное (рис.2) и параллельное (рис.3):

Рис.2

Полное сопротивление цепи, состоящей из нескольких последовательно соединенных проводников, равно сумме сопротивлений этих проводников:

(7)

Полная проводимость параллельно соединенных проводников равна сумме проводимостей этих проводников:

(8)

Для расчета разветвленной цепи, в которой произвольно размещены сопротивления и источники тока, не достаточно применения закона Ома и формул (7) и (8). В этом случае можно применить два правила Кирхгофа.

Первое правило Кирхгофа: алгебраическая сумма сил тока в узле разветвления равна нулю:

Под узлом разветвления понимают такие точки цепи, в которых сходится не менее трех проводников. Токи, входящие в узел, условно считают положительным, а токи, выходящие из узла, - отрицательными.

Под узлом разветвления понимают такие точки цепи, в которых сходится не менее трех проводников. Токи, входящие в узел, условно считают положительными, а токи, выходящие из узла, - отрицательными.

Второе правило Кирхгофа: в замкнутом контуре разветвленной цепи алгебраическая сумма электродвижущих сил источников тока равна алгебраической сумме произведений сил тока на сопротивления соответствующих участков этого контура:

При этом также следует строго придерживаться правила знаков: токи, идущие вдоль выбранного направления обхода (в данном случае по часовой стрелке), считается положительными, а идущие против направления обхода – отрицательными. Электродвижущая сила считается положительной, если она создает ток в положительном направлении обхода контура, в противном случае эдс имеет отрицательный знак.

II. Описание экспериментальной установки.

Одним из наиболее точных способов измерения сопротивлений является метод моста Уитстона. Мост (рис.4) состоит из реохорда АС, гальванометра G, магазина сопротивлений R₀, исследуемого сопротивления R _х, ключа замыкания К и источника Б.

Рис.4

Реохорд АС выполнен из однородной проволоки, сечение которой неизменно по всей ее длине. Скользящий контакт Д. дает возможность изменять длину плеч реохорда l ₁ и l ₂ и тем самым изменять сопротивление участков АД и ДС.

Запишем первое правило Кирхгофа для узлов В и Д. и второе правило для контуров АВДА и ВСДВ:

для узла В –

для узла Д. – (11)

для контура АВДА –

для контура ВСДВ – (12)

Пусть ток в гальванометре отсутствует, т. е. J_g = 0

Тогда формулы (11) и (12) примет вид: