 |
Краткие теоретические сведения.
|
|
|
|
Жидкости, как газы и твердые тела, состоят из мельчайших частиц – молекул, между которыми действуют силы взаимного притяжения и отталкивания. Силы молекулярного взаимодействия быстро убывают с увеличением расстояния от молекулы и уже на расстоянии R, равном 10-7см, практически не проявляются (радиус самих молекул r = 0,5*10-7см).
Расстояние R, называется радиусом молекулярного действия, а сферу радиусом R – сферой молекулярного действия.
Молекула, находящаяся внутри жидкости, испытывает одинаковое взаимодействие со стороны молекул, окружающих ее со всех сторон. Равнодействующая молекулярных сил, действующих на нее, будет равна нулю. Если же молекула расположена на поверхности жидкости, то равновесие нарушается: притяжение со стороны молекул, лежащих внутри жидкости больше и равнодействующая молекулярных сил направлена внутрь жидкости F1,2 . (рис 1).

Рис.1
Молекулярные силы, действующие на все частицы, лежащие в тонком поверхностном слое, толщина которого равна радиусу сферы действия молекулы, складываясь между собой, оказывают на поверхность жидкости некоторое давление, которое называют молекулярным давлением. Все молекулы, находящиеся в поверхностном слое жидкости, подвержены действию этих сил, стремящихся втянуть их внутрь жидкости.
Таким образом, под действием молекулярных сил, направленных внутрь жидкости, поверхностный слой жидкости находится в особом, напряженном состоянии, напоминая собой напряжение растянутой пленки, стремящейся сократиться.
Чтобы переместить молекулу из глубины на поверхность жидкости, надо совершить работу против результирующей силы молекул в поверхностном слое. В результате молекулы на поверхности жидкости обладают определенной потенциальной энергией, называемой свободной поверхностной энергией. Если на жидкость не действуют внешние силы, то значение свободной поверхностной энергии оказывается минимальным; при этом минимальна и площадь и самой поверхности. Капли жидкости в невесомости имеют форму шариков (минимальная площадь поверхности). В земных условиях действует сила тяжести, которая пытается сдавить каплю, в результате чего она принимает форму эллипса.
|
|
|
Работа, которую нужно совершить для увеличения свободной поверхности жидкости будет равна:

где α – коэффициент поверхностного натяжения.
По своему физическому смыслу α является работой, которую надо затратить, чтобы увеличить поверхность жидкости на единицу при сохранении ее объема неизменным. Коэффициент поверхностного натяжения α измеряется в системе СИ в Дж/м2.
Для того, чтобы поверхностную пленку удержать в равновесии, нужна определенная сила F, приложенная касательно к поверхности жидкости. Она будет тем больше, чем больше длина ℓ, ограничивающей поверхности пленки:
F = α *ℓ (1)
где α – коэффициент поверхностного натяжения.
Из формулы (1) следует, что
α =  ,
,
т. е. коэффициент поверхностного натяжения жидкости численно равен силе поверхностного натяжения, действующей на единицу длины контура, ограничивающего поверхность жидкости. Из (2) видно, что α измеряется в Н/м. Коэффициент поверхностного натяжения жидкости имеет порядок 10-2- 10-1Н/м; для воды он равен 0,073 Н/м, а для ртути 0,54 Н/м. С повышением температуры коэффициент поверхностного натяжения уменьшается в связи с увеличением среднего расстояния между молекулами жидкости.
Когда жидкость налита в сосуд, то между молекулами стенок сосуда и молекулами поверхности жидкости действуют силы притяжения Fα (адгезии, т. е. силы прилипания молекул двух различных тел, вызванные взаимным притяжением), Fк они приводят к возникновению краевого угла θ между стенками сосуда и поверхностью жидкости. Равнодействующая сил когезии и адгезии Fα и Fк всегда перпендикулярна поверхности жидкости (рис. 2).
|
|
|

Рис.2
Из рис. 2 видно, что равнодействующая этих сил F может иметь различное направление, в результате чего поверхность жидкости может быть вогнутой, выпуклой или горизонтальной. Если жидкость смачивает стенки, то силы когезии Fк меньше, чем силы адгезии Fα; результирующая сила направлена из жидкости. В этом случае поверхность имеет вогнутую форму.
В не смачивающей жидкости, по аналогичным соображениям поверхность жидкости примет выпуклую форму.
Если Fα = Fк, то поверхность жидкости горизонтальна.
Под искривленной поверхностью жидкости, помимо внутреннего давления Р., создается еще дополнительное давление ΔР, обусловленное кривизной поверхности (рис. 3). Это добавочное давление всегда направлено к центру кривизны поверхности. Если жидкость имеет выпуклую поверхность, то добавочное давление направлено вовнутрь жидкости и общее давление в жидкости в этом случае будет больше, чем под горизонтальной поверхностью.

Рис.3
Если поверхность жидкости имеет вогнутую форму, то добавочное давление направлено к центру кривизны, находящемуся вне жидкости, и общее давление здесь меньше, чем под горизонтальной поверхностью.
Добавочное давление для сферической поверхности определяется по формуле Лапласа:
ΔР = 
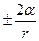 ,
,
где ΔР – добавочное давление,
α – коэффициент поверхностного натяжение,
r – радиус кривизны поверхности жидкости.
2. Описание экспериментальной установки
В данной работе определения коэффициента поверхностного натяжения жидкости используется метод отрыва капель.
Испытуемая жидкость медленно по каплям вытекает из узкого отверстия тонкой стеклянной трубки (бюретки), установленной вертикально на штативе. Поверхностная пленка, образующаяся в отверстии, оказывает сопротивление вытеканию жидкости. Под давлением вышележащих слоев жидкости пленка растягивается, и жидкость собирается в каплю на конце трубки (рис.4).
На каплю действует сила тяжести P=mg, направленная вертикально вниз, и сила поверхностного натяжения F, действующая вверх. Пока капля удерживается на конце отверстия, сила Fбольше по величине, чем сила тяжести P. Так как жидкость вытекает из трубки, то капля будет увеличиваться в размере, и сила тяжести будет возрастать. Наступит такой момент, когда сила будет находиться в покле. Но как только Р. незначительно превысит силу поверхностного натяжения F, капля оторвется и упадет.
|
|
|
Пир вычислении считаем, что момент отрыва Р. = F, а силу поверхностного натяжения F можем определить по формуле (1):
F= α ℓ
где ℓ - длина контура, по которому разрывается поверхностный слой жидкости,
а он равен длине окружности в месте перетяжки (рис. 4).

Рис.4
Если радиус перетяжки обозначить через r, то ℓ=2πr и тогда запишем:
mg = α2πr
Тогда
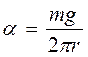 ,
,
Эта формула является расчетной для α.
3. Порядок выполнения работы.
1. Взвесьте на технических весах чистый сухой стаканчик и определите его массу m1.
2. Налейте в бюретку исследуемую жидкость.
3. Подставьте под бюретку второй стакан и отрегулируйте кран так, чтобы жидкость вытекала каплями (примерно 30 капель в минуту). 
4. Подставьте под бюретку взвешенный стаканчик: наберите в него n капель исследуемой жидкости (число капель задается преподавателем).
5. Определите массу стаканчика с каплями m2.
6. Вычислите массу одной капли по формуле:


7. Опыт повторите 3 раза и найдите среднее значение массы одной капли m.
8. Вычислите коэффициент поверхностного натяжения по формуле (3) (радиус перетяжки написан на бюретке).
9. Рассчитайте ошибки измерений по формулам:


10.Данные измерений и вычислений занесите в таблицу I:
Таблица 1
Результаты эксперимента
| 1. | |||||||||
| 2. | |||||||||
| 3. | |||||||||
| Ср. |
11. Запишите ответ в виде:

12.Сделайте выводы.
КОНТРОЛЬНЫЕ ВОПРОСЫ.
1. Чем обусловлено возникновение дополнительного давления? Запишите формулу Лапласа.
|
|
|
2. Объясните молекулярно-кинетический механизм поверхностного натяжения.
3. От каких факторов зависит коэффициент поверхностного натяжения?
4. Что такое внутреннее давление жидкости?
5. Что такое поверхностно-активные вещества и где они применяются?
6. Объясните капиллярные явления. От чего зависит высота поднятия (опускания) столба жидкости в капилляре?
7. Выведите формулу Жюрена.
8. Объясните явления смачивания и несмачивания.
ЛАБОРАТОРНАЯ РАБОТА № 9
ОПРЕДЕЛЕНИЕ ОТНОШЕНИЯ ТЕПЛОЕМКОСТЕЙ ВОЗДУХА (Ср/Су) МЕТОДОМ КЛЕМАНА И ДЕЗОРМА
ЦЕЛЬ РАБОТЫ:изучение законов идеального газа, первого начала термодинамики, ознакомление с понятием газового цикла и определение отношения теплоемкостей воздух g = Ср/Сv
ПРИБОРЫ И ПРИНАДЛЕЖНОСТИ:установка для определения отношения теплоемкостей.
|
|
|


