 |
Построение и использование компьютерных моделей на занятиях по информатике
|
|
|
|
Самое главное и сложное в компьютерном моделировании - это построение или выбор той или иной модели.
При построении компьютерной модели используют системный подход, который заключается в следующем. Рассмотрим объект - солнечную систему. Систему можно разбить на элементы - Солнце и планеты. Введем отношения между элементами, например, удаленность планет от Солнца. Теперь можно рассматривать независимо отношения между Солнцем и каждой из планет, затем обобщить эти отношения и составить общую картину солнечной системы (принципы декомпозиции и синтеза).
Некоторые характеристики моделей являются неизменными, не меняют своих значений, а некоторые изменяются по определенным законам. Если состояние системы меняется со временем, то модели называют динамическими, в противном случае - статическими.
Построение компьютерной модели. Моделирование
При построении моделей используют два принципа: дедуктивный (от общего к частному) и индуктивный (от частного к общему).
При первом подходе рассматривается частный случай общеизвестной фундаментальной модели. Здесь при заданных предположениях известная модель приспосабливается к условиям моделируемого объекта. Например, можно построить модель свободно падающего тела на основе известного закона Ньютона ma = mg-Fсопр и в качестве допустимого приближения принять модель равноускоренного движения для малого промежутка времени.
Второй способ предполагает выдвижение гипотез, декомпозицию сложного объекта, анализ, затем синтез. Здесь широко используется подобие, аналогичное моделирование, умозаключение с целью формирования каких-либо закономерностей в виде предположений о поведении системы. Например, подобным способом происходит моделирование строения атома. Вспомним модели Томсона, Резерфорда, Бора.
|
|
|
Технология построения модели при дедуктивном способе:
Теоретический этап:
а) оценки;
б) аналогии;
в) подобие.
Знания, информация об объекте (исходные данные об объекте).
Постановка задачи для целей моделирования.
Выбор модели (математические формулировки, компьютерный дизайн).
Технология построения модели при индуктивном способе:
Эмпирический этап:
а) умозаключение;
б) интуиция;
в) предположения;
г) гипотеза.
Постановка задачи для моделирования.
Оценки. Количественное и качественное описание
Построение модели.
Этапы решения задачи с помощью компьютера (построение модели - формализация модели - построение компьютерной модели - проведение компьютерного эксперимента - интерпретация результата).
Основные этапы разработки и исследования моделей на компьютере
· описательная информационная модель
· формализованная модель
· компьютерная модель
· компьютерный эксперимент
Анализ полученных результатов и корректировка исследуемой модели
этап - описательная информационная модель: такая модель выделяет существенные (с точки зрения целей проводимого исследования) параметры объекта, а несущественными параметрами пренебрегает
этап - Описательная информационная модель записывается с помощью какого-либо формального языка. В такой модели с помощью формул, уравнений, неравенств и пр. фиксируются формальные соотношения между начальными и конечными значениями свойств объектов, а также накладываются ограничения на допустимые значения этих свойств.
этап - компьютерная модель
Описательная информационная модель записывается с помощью какого-либо формального языка.
В такой модели с помощью формул, уравнений, неравенств и пр. фиксируются формальные соотношения между начальными и конечными значениями свойств объектов, а также накладываются ограничения на допустимые значения этих свойств.
|
|
|
Пути построения компьютерной модели
Построение алгоритма решения задачи и его кодирование на одном из языков программирования;
Построение компьютерной модели с использованием одного из приложений (электронных таблиц, СУБД и пр.)
этап - компьютерный эксперимент
Если компьютерная модель существует в виде программы на одном из языков программирования, её нужно запустить на выполнение и получить результаты.
Если компьютерная модель исследуется в приложении, например в электронных таблицах, можно провести сортировку или поиск данных, построить диаграмму или график.
этап - анализ полученных результатов и корректировка исследуемой модели
В случае различия результатов, полученных при исследовании информационной модели, с измеряемыми параметрами реальных объектов можно сделать вывод, что на предыдущих этапах построения модели были допущены ошибки или неточности.
Провести корректировку модели.
Метод имитационного моделирования (метод Монте-Карло)
Теоретическая основа метода была известна давно. Однако до появления ЭВМ этот метод не мог найти сколько-нибудь широкого применения, ибо моделировать случайные величины вручную - очень трудоемкая работа.
Само название «Монте-Карло» происходит от города Монте-Карло в княжестве Монако, знаменитого своим игорным домом. Дело в том, что одним из механических приборов для получения случайных величин является рулетка. Для вычисления площади круга единичного радиуса проведем эксперимент.
Рассмотрим практическую задачу.
В качестве примера построения компьютерной модели рассмотрим тему «Определение параметров светофорного регулирования при пропуске транспорта через узкий участок дороги с использованием светофора».
На рис. 1 представлена расчетная схема
Исходные данные
Интенсивность встречных потоков - N1=420 ед/ч, N2=570 ед/ч;
Длина узкого участка - Lk=300 м;
Расчетные скорости - V1=9,72 м/с, V2=13,88 м/с;
Расчетная длина автомобиля - La=2,5 м;
Коэффициент сцепления ц = 0,6;
Время реакции водителей и срабатывания тормозного привода - tp=0,6с;
|
|
|
Интервал безопасности между автомобилями - l0=2 м;
Ускорение свободного падения - g = 9,8 м/с2.
Изменяющийся параметр
Интенсивность потока, N1
| Конечное значение | Шаг изменения | |
| 425 | 575 | 25 |
Расчетные формулы
1. 
, м, остановочный путь для потоков N1, N2
. 
, м, динамический габарит в i-том направлении
. 
, с, временной интервал между автомобилями по i-тому направлению
. 
, с, суммарное время горения сигнала за 1 час, необходимое для пропуска заданной интенсивности Ni
. 
, с, длительность переходного интервала в i-й фазе
. 
, с, суммарное время переходных интервалов в соответствующей фазе за 1 час
. 
, число циклов за 1 час; (выделена целая часть числа)
Расчетная таблица
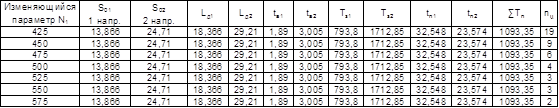
Диаграмма зависимости числа светофорных циклов от изменяющегося параметра
Максимальное расчетное часовое значение числа светофорных циклов достигается при интенсивности потока Т1=425 ед/ч
Заключение
В данной курсовой работе проведено изучение вопроса об обучении построению и использованию компьютерных моделей в базовом курсе информатики.
В ходе выполнения курсовой работы раскрыты следующие вопросы:
− проведен анализ понятий, связанных с математическим моделированием;
− рассмотрены различные классификации математических моделей;
− раскрыт вопрос о компьютерном математическом моделировании;
− рассмотрен вопрос о моделировании в курсе «Информатика и ИКТ»;
− изучен вопрос о построении и использовании компьютерных моделей на занятиях по информатике.
Таким образом, подводя итог всему вышесказанному можно ответить на вопрос: для чего нужны модели? Модели нужны для того, чтобы:
− понять, как устроен объект (его структура, свойства, законы развития, взаимодействия с окружающим миром).
− научиться управлять объектом (процессом) и определять наилучшие стратегии
− прогнозировать последствия воздействия на объект.
Модель позволяет получить новые знания об объекте, но, в подавляющем большинстве случаев, в той или иной степени она не полна.
|
|
|
Модель, сформулированная на языке математики с использованием математических методов называется математической моделью.
Исходным пунктом ее построения обычно является некоторая задача, например экономическая. Широко распространены, как дескриптивные, так и оптимизационные математические, характеризующие различные экономические процессы и явления, например:
− распределение ресурсов
− рациональный раскрой
− транспортные перевозки
− укрупнение предприятий
− сетевое планирование.
На основании проведенного исследования можно сделать следующие основные выводы:
− имитационное моделирование не заменяет методы оптимизации, а удобно дополняет их;
− компьютерная модель исполняет роль вспомогательного средства для решения задач;
− компьютерная модель исполняет роль средства конструирования компьютерных обучающих и моделирующих сред;
− исполняет роль средства моделирования для получения новых знаний.
Практическая значимость работы состоит в том, что она позволила мне глубже изучить и усвоить вопрос об обучении построению и использованию компьютерных моделей в базовом курсе информатики.
Полученные знания можно использовать в педагогической практике и, таким образом, давать более глубокие и полные знания ученикам.
В качестве рекомендации относительно возможностей практического применения материалов работы считаю перспективным разработать программный продукт и использовать его для обучения учеников построению и использованию компьютерных моделей в базовом курсе информатики в школе.
Список использованной литературы
1. Анищенко, В.С. Динамические системы / В.С. Анищенко // Соросовский образовательный журнал. - 2007. - №11. - М. - С. 77-84
2. Васильков, Ю.В. Компьютерные технологии моделирования: учеб. пособие / Ю.В. Васильков - М.: Финансы и статистика, 2010. - 256 с.
. Введение в математическое моделирование: учебное пособие / под ред. П.В. Трусова; рецензенты: А.Р. Абдулаев, В.П. Матвиенко; Министерство образования РФ. - М.: Логос, 2004. - 440 с.
. Данилов, Ю.А. Лекции по нелинейной динамике. Элементарное введение: учеб. пособие / Ю.А. Данилов.; - 2-е изд. - М.: КомКнига, 2011. - 208 с.
. Новик, И.Б. О философских вопросах кибернетического моделирования / И.Б. Новик - М.: Знание, 1964.
. Самарский, А.А. Математическое моделирование: Идеи. Методы. Примеры / А.А. Самарский, А.П. Михайлов - М.: Физматлит, 2009. - 320 с.
. Севостьянов, А.Г. Моделирование технологических процессов: учебник / А.Г. Севостьянов, П.А. Севостьянов. - М.: Легкая и пищевая промышленность, 1984. - 344 с.
|
|
|
. Советов, Б.Я. Моделирование систем: учебник для ВУЗов / Б.Я. Советов, С.А. Яковлев - 3-е изд., перераб. и доп. - М.: Высшая школа, 2011. - 343 с.
. Экштайн, В. Компьютерное моделирование взаимодействия частиц с поверхностью твердого тела / В. Экштайн; пер. с англ. М.Г. Степановой; под ред. Е.С. Машковой. - М.: Мир, 2009. - 319 с.
|
|
|
