 |
Построение графика суммарной работы и определение момента сил сопротивления.
|
|
|
|
На корпусе двигателя установлен ряд вспомогательных систем и устройств таких как системы смазки, охлаждения и.т.д. дополнительные потери возникают из за трения в подшипниках, на стенках цилиндра, взбалтывания масла. Из за постоянного характера этих потерь приведенный момент сил сопротивления предполагается постоянным. Работа движущего момента за цикл  = 165.8 Дж (найдено при помощи численного интегрирования функции изменения приведенного момента движущих сил методом трапеций).
= 165.8 Дж (найдено при помощи численного интегрирования функции изменения приведенного момента движущих сил методом трапеций).
Суммарная работа движущих сил и сил сопротивления за цикл равна нулю (режим установившийся). В соответствии с законом сохранения энергии:
|
Следовательно, Mc=12 Н*м.
Момент сопротивления показан на графике приведенных моментов.
Строим график работы движущего момента за цикл, а также график работы сил сопротивления. Масштаб графика определяем по формуле
mА=mМ *mf/К=0,48 мм/Дж,
где К=40 мм-отрезок интегрирования.
Выполнение перехода от графика суммарного приведенного момента инерции второй группы звеньев к приближенному графику кинетической энергии той же группы звеньев.
Определяли кинетическую энергию  через приведенные моменты инерции этой же группы звеньев. Закон изменения
через приведенные моменты инерции этой же группы звеньев. Закон изменения  на данном этапе неизвестен, поэтому для определения
на данном этапе неизвестен, поэтому для определения  воспользовались приближенным равенством
воспользовались приближенным равенством  , поскольку коэффициент неравномерности
, поскольку коэффициент неравномерности  - величина малая.
- величина малая.
Тогда: 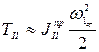
Так как 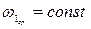 , то
, то  можно считать пропорциональной
можно считать пропорциональной  , а построенную кривую
, а построенную кривую 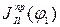 принять за приближенную кривую
принять за приближенную кривую  .
.
Масштаб  находим по формуле m
находим по формуле m  =2*mJ /w1cp2 *mJS =20 мм/Дж.
=2*mJ /w1cp2 *mJS =20 мм/Дж.
Построение приближенного графика кинетической энергии звеньев первой группы.
Согласно уравнению  имеем
имеем 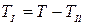
|
|
|
Следовательно, для механизма двигателя при построении кривой  из ординат кривой
из ординат кривой  в каждом положении механизма вычитали отрезки, изображающие величины
в каждом положении механизма вычитали отрезки, изображающие величины  ; взятые из графика
; взятые из графика  ; вычитаемые отрезка представляли в том же масштабе
; вычитаемые отрезка представляли в том же масштабе  , в каком построена кривая
, в каком построена кривая  . Полученная кривая
. Полученная кривая  - приближенная, так как построена вычитанием из точной кривой
- приближенная, так как построена вычитанием из точной кривой  приближенных значений
приближенных значений  .
.
Определение необходимого момента инерции маховых масс.
На кривой  нашли точки, соответствующие значениям
нашли точки, соответствующие значениям  и
и  , и согласно этим значениям максимальное изменение кинетической энергии I группы звеньев за период цикла:
, и согласно этим значениям максимальное изменение кинетической энергии I группы звеньев за период цикла:  ,
,
где  - отрезок в мм, изображавший
- отрезок в мм, изображавший  в масштабе
в масштабе 
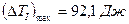 .
.
Необходимый момент инерции  подсчитали по формуле
подсчитали по формуле
 =
=  /(w1cp2*d)=
/(w1cp2*d)= 
Построение графика угловой скорости.
При определении закона движения воспользовались тем, что при малых значениях коэффициента неравномерности  верхняя часть графика
верхняя часть графика  , изображающая изменение кинетической энергии
, изображающая изменение кинетической энергии  , приближенно изображает также изменение угловой скорости
, приближенно изображает также изменение угловой скорости  .
.
В точках P и Q кривой  имеет соответственно значения
имеет соответственно значения 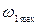 и
и  . Масштаб графика угловой скорости определяется по формуле:
. Масштаб графика угловой скорости определяется по формуле: 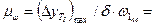 41/(141.3*1/15)=4.3, где ω1ср=2*π*nхх=141.3 рад/с.
41/(141.3*1/15)=4.3, где ω1ср=2*π*nхх=141.3 рад/с.
Чтобы перейти от изменений угловой скорости к ее полному значению, определили положение оси абсцисс графика  . Для этого через середину отрезка PQ, изображающего разность
. Для этого через середину отрезка PQ, изображающего разность  , провели горизонтальную штриховую линию, которая является линией средней угловой скорости
, провели горизонтальную штриховую линию, которая является линией средней угловой скорости  . Расстояние от линии
. Расстояние от линии  до оси абсцисс определялось следующим образом:
до оси абсцисс определялось следующим образом:
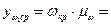

Получив положение оси абсцисс графика  , можно определить
, можно определить  ,а по ней и
,а по ней и 
 Дж.
Дж.
Силовой расчет механизма.
Силовой расчет производиться при холостом режиме.
Силовой расчёт производим методом планов сил, который представлен на листе 2. Для этого сначала строим планы скоростей и ускорений для левой и правой частей двигателя.
Решение методом планов производиться при угловой координате кривошипа  .Также известно Fд5=4000 Н, Fд3=0.
.Также известно Fд5=4000 Н, Fд3=0.
|
|
|
3.1. Построение планов скоростей.
По графику  для
для 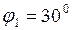 нашли
нашли  .
.
Построили план скоростей для положения 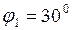 в масштабе
в масштабе  , и определили величины и направления скоростей точек
, и определили величины и направления скоростей точек  :
:
 , где
, где 
 ,
,
 , где
, где  ;
;
Аналогично:
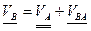 , где;
, где; 
 ,
,
 , где
, где  ;
;
3.2. Построение планов ускорений.
Построили планы ускорений по векторным уравнениям в выбранном масштабе ускорений 
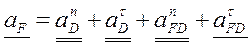 ;
;
 ,
,

 ;
;
Аналогично для точки В:
 ;
;
 ;
;
|
|
|



