Основыне законы и постулаты алгебры логики.

46.Определение булевой функции. Булевы функции двух переменных.

Булевой функцией от n аргументов называется функция f из n -ой степени множества { 0, 1 } в множество { 0, 1 }.

Иначе говоря, булева функция – это функция, и аргументы и значение которой принадлежит множеству { 0, 1 }

Элементы булева множества {1, 0} обычно интерпретируют как логические значения «истинно» и «ложно».

Булевы функции называются также функциями алгебры логики, двоичными функциями и переключательными функциями.

 

Булевы функции находят применение в конструировании и упрощении логических схем. Такие схемы встречаются в электронных устройствах, используе­мых в компьютерах, калькуляторах, телефонных системах и ряде других устройств.

Обозначим множество {0;1} через 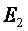, т. е. .

Функция f из множества называется булевой функцией n переменных. Напомним, что

Переменные булевых функций могут принимать только значения 0 или 1 и называются булевыми переменными.

Множества всех булевых функции n переменных обозначается , т.е.

.

Количество всех булевых функции n переменных находится по формуле

.

Например, булевые функции 2 переменных

,

Булевы функции часто задаются таблично. Эти таблицы напоминают таблицы истинности логических операций, поэтому сами булевы функции часто называют булевыми операциями, а соответствующие им таблицы - таблицами истинности.

Булевы функции двух переменных

		Значения переменных	x1
x2
	Название функции	Обозначение функции	Значения функции
f 1	Тождественный нуль
f 2	Конъюнкция	&, , ·
f 3	Отрицание импликации
f 4	Тождественная первой переменной
f 5	Отрицание импликации
f 6	Тождественная второй переменной
f 7	Сумма по модулю два, строгая дизъюнкция	,
f 8	Дизъюнкция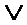
f 9	Стрелка Пирса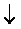
f 10	Эквиваленция	, , ~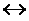
f 11	Инверсия второй переменной
f 12	Импликация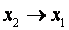
f 13	Инверсия первой переменной
f 14	Импликация
f 15	Штрих Шеффера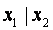
f 16	Тождественная единица

 

Переключательная схема. Элементы переключательной схемы.

Переключательная схема – схематическое изображение некоторого устройства, состоящего из переключателей и соединяющих их проводников, а также входов и выходов, на которые подаётся и с которых снимается электрический сигнал.

 

Каждый переключатель имеет только два состояние: замкнутое и разомкнутое. Всей переключательной схеме также можно поставить в соответствии логическую переменную «х», равную единице, если схема проводит ток, и равную нолю – если не проводит. Эта переменная является функцией от переменных, соответствующих всем переключателям схемы, и называется функцией проводимости.

Виды схем:

a) Схема не содержит переключателей и, следовательно, проводит ток всегда (F = 1);

b) Схема содержит один постоянно разомкнутый контакт (F = 0);

c) Схема проводит ток, когда переключатель «х» замкнут, и не проводит, когда «х» разомкнут (F(x) = x);

d) Схема проводит ток, когда переключатель «х» разомкнут, и не проводит, когда «х» замкнут (F(x) = не х)

e) Схема проводит ток, когда оба переключателя замкнуты (F(x) = x*y);

f) Схема проводит ток, когда хотя бы один из переключателей замкнут (F(x) = x v y) (здесь «+», но надо будет записать так);

g) Схема состоит из двух параллельных ветвей (F (x, y, z) = (x * не y) v z v (не х * у) * не z).

 

Как выглядят схемы посмотрите в учебнике Акулина на страницах 126-127.

Синтез переключательной схемы по заданным условиям ее работы.

Синтез переключательной схемы по заданным условиям её работы сводится к следующим трём этапам:

1. Составление функции проводимости по заданным условиям;

2. Упрощение этой функции;

3. Построение соответствующей функции.

 

Дальше банально идут задачи и их решение. В этом вопросе вообще больше нечего писать.

Таблица истинности.

Таблица истинности — это таблица, которая описывает логическую функцию. Логическая

функция здесь — это функция, у которой значения переменных и значение самой функции

выражают истинность. Например, они принимают значения «истина» либо «ложь»

Для каждого составного высказывания (логического выражения) можно построить таблицу

истинности, которая определяет его истинность или ложность при всех возможных комбинациях

исходных значений простых высказываний (логических переменных).

Таблицы истинности применяются для определения значения какого-либо высказывания для

всех возможных случаев значений истинности высказываний, которые его составляют.

Количество всех существующих комбинаций в таблице находится по формуле N=2*n; где N -

общее количество возможных комбинаций, n - число входных переменных.

Таблицы истинности нередко используются в цифровой технике и булевой алгебре, чтобы

описать работу логических схем.

Таблицы истинности для основных функций:

1.Схема И- КонъюнкцияЕдиница на выходе Схемы И будет тогда и только тогда, когда на всех входах будут единицы.

Когда хотя бы на одном входе будет ноль, на выходе также будет ноль.

Операция конъюнкции на структурных схемах обозначается знаком & (читается как амперсэнд),

являющимся сокращенной записью английского слова end.

2. Схема ИЛИ-Д изъюнкция

Схема ИЛИ. Эта схема реализует дизъюнкцию двух или более логических значений. Когда хотя

бы на одном входе Схемы ИЛИ будет единица, на ее выходе также будет единица.

Знак 1 на схеме соответствует обозначению, т. е. значение дизъюнкции равно единице, если

сумма значений операндов больше или равна 1.

3. СхемаНЕ-Схема НЕ (инвертор) реализует операцию ОТРИЦАНИЯ.

Если на входе схемы 0, то на выходе 1. Когда на входе 1, на выходе 0.

6. Схема ЕСЛИ …ТО – Импликация

Импликация записывается как посылка → следствие

истинна в трех случаях:

1) ее основание a и ее следствие b истинны;

2) основание a ложно, а следствие b истинно;

3) и основание a и следствиеb ложны.

Только в одном случае, когда основание a истинно, а следствие b ложно, вся импликация ложна

Последовательность построения (составления) таблицы истинности:

1.Определить количество N используемых переменных в логическом выражении. Количество

строк в таблице истинности равно количеству возможных комбинаций значений логических

переменных, входящих в логическое выражение.

2. Вычислить количество всевозможных наборов значений переменных M = 2N, равное

количеству строк в таблице.

3. Подсчитать количество логических операций в логическом выражении и определить

количество столбцов в таблице, которое равно количеству переменных плюс количество

логических операций.

4. Озаглавить столбцы таблицы названиями переменных и названиями логических операций.

5. Заполнить столбцы логических переменных наборами значений, например, от 0000 до 1111 с

шагом 0001 в случае для четырех переменных.

6.Заполнить таблицу истинности по столбцам со значениями промежуточных операций слева

направо.

7. Заполнить окончательный столбец значений для функции F. Таким образом, можно составить

(построить) таблицу истинности самостоятельно.

 

⇐ Предыдущая1234567Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: