Алгебраический и векторный момент силы относительно точки. Равенство векторного момента пары сил и векторного момента силы относительно точки

Алгебраическим моментом силы относительно точки называют произведение модуля силы на плечо силы относительно этой точки, взятое со знаком плюс или минус M0(F)=F*h

Векторным моментом силы относительно точки называют вектор приложенный в этой точке и равный по модулю, произведению силы на плечо силы относительно этой точки. Векторный момент направлен перпендикулярно плоскости, в которой лежат сила и точка, таким образом, что с его конца можно видеть "стремление" силы вращать тело против движения часовой стрелки.

Mz(F)=Mo(F)*cosα Момент силы, относительно оси равен прекции вектора момента сил, относительно точки оси на эту ось.

Параллельный перенос силы. Пример(доказательство)

Теорема - силу, приложенную к абсолютно твердому телу, можно, не изменяя оказываемого ею действия, переносить из данной точки в любую другую точку тела, прибавляя при этом пару с моментом, равным моменту переносимой силы относительно точки, куда сила переносится.

Пусть на твердое тело действует сила F, приложенная в точке А. Действие этой силы не изменяется, если в любой точке B тела приложить две уравновешенные силы F`и F`` такие, что F`=F, F``=-F. Полученная система трех сил и представляет собой силу F, равную F, но приложенную в точке В, и пару F, F с моментом

Пример. На барабан 1 радиуса r намотаны в противоположных направлениях две нити, к концам которых прикладывают силы F и F`=-F; на барабан 2 того же радиуса намотана одна нить, к которой прикладывают силу, равную 2F. Рассмотрим, чем будут отличаться действия этих сил. На барабан 1 действует только пара сил F, F` с моментом, численно равным 2Fr вращающая барабан. Силу, действующую на барабан 2, можно заменить силой 2F`=2F приложенной к оси барабана, и парой 2F,2F`` В результате находим, что на этот барабан действуют: 1) пара с численно таким же, как и в первом случае, моментом 2Fr вращающая барабан, и 2) сила 2F` оказывающая давление на ось барабана.

Итак, оба барабана будут вращаться одинаково. Но при этом ось второго барабана испытывает давление, равное 2F, а ось первого барабана никакого давления не испытывает.

Основная теорема статики (о приведении произвольной системы сил (ПСС) к данному центру). Условия равновесия ПСС в векторной форме. Частные случаи равновесия

Теорема о приведении системы сил: любая система сил, действующих на абсолютное твердое тело, при приведении к произвольному выбранному центру О, заменяется одной силой R, равной главному вектору системы сил и приложенной в центре приведения О, и одной парой с моментом М,равным главному моменту системы сил относительно О

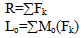,где R- главный вектор системы сил

Lо- главный моментом системы сил(вместо Lo- писать Mo, а вместо Мо-mо)

Условия равновесия можно сформулировать так: для равновесия произвольной системы сил, приложенных к твердому телу, необходимо и достаточно, чтобы суммы проекций всех сил на оси декартовой системы координат равнялись нулю и суммы моментов всех сил относительно этих осей также равнялись нулю. Т.е. чтобы выполнялось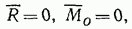

Частные случаи. Условия равновесия пространственной системы параллельных сил.

Если силы, действующие на твердое тело, параллельны между собой, то можно выбрать такую систему координат, когда одна из ее осей, например Oz, параллельна направлению действия сил. Тогда из шести аналитических условий равновесия три выполняются тождественно, и система параллельных сил будет иметь только три условия равновесия:

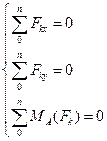1-ая форма 2-ая форма 3-ья форма