 |
Обработка результатов прямых измерений
|
|
|
|
Лабораторная работа №1
«Оценка погрешностей прямых и косвенных измерений при изучении колебаний математического маятника»
Цель: Вычисление средних значений измеряемых величин и доверительного интервала прямых и косвенных измерений при заданной доверительной вероятности.
Приборы и принадлежности:
- Математический маятник на штативе;
- Линейка деревянная 0-500мм, цена деления 1мм, класс точности не установлен;
- Секундомер телефона IPhone 3, цена деления 0,1с.
Теоретические сведения
Измерение величин – это установление численного соотношения между измеряемой величиной и единицей измерения, которое показывает, сколько эталонных единиц измерения содержится в измеряемой величине.
Измерения делятся по способу получения – прямые и косвенные.
Прямые измерения – это те, при которых искомое значение величины получают исходя из прямых опытных данных, с помощью измерительных приборов.
Косвенные измерения – те, которые получают на основании прямых измерений, путем вычисления по определенной функциональной зависимости. Косвенные измерения применяются там, где провести прямые не представляется возможным, либо точность прямых измерений слишком низка. Пример: вычисление объемов геометрических фигур исходя из их размеров.
Ошибки измерений. При проведении любых измерений невозможно избежать разного рода ошибок и погрешностей. Ошибки принято делить на следующие:
Систематические – являются следствием неправильной калибровки прибора. Проявляются при каждом измерении и вызывают отклонения в одну и ту же сторону на одну и ту же величину. Измерить их величину можно сравнивая результаты измерений с результатами, полученными исправным прибором.
|
|
|
Случайные – являются следствием изменчивости условий измерения, несовершенством органов чувств.
Промахи – случайные ошибки, вызванные невнимательностью измеряющего.
Приборные погрешности – каждый прибор имеет свой ограниченный класс точности, устанавливающий границы разброса получаемых данных и допускающий получение погрешностей в этих рамках.
Любое проводимое измерение является ошибочным, истинная величина всегда остается неизвестной. Вычисление абсолютной ошибки:
Δxi = xист - xi,
где Δxi – абсолютная ошибка, xист – истинное значение, которое всегда остается неизвестным, xi – результат измерения.
Относительная ошибка – отношение абсолютной ошибки к истинному значению измеряемой величины:
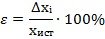
Наличие погрешностей ограничивает достоверность измерений. Для установления границ погрешностей необходима обработка результатов, которая основывается на законах математической статистики.
Обработка результатов прямых измерений
При проведении измерений в одинаковых условиях и с одинаковой точностью, для оценки xист используется среднее арифметическое результатов всех измерений:
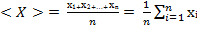. (1)
Среднее арифметическое <x> – результат измерений.
Поскольку результаты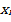 
– величины случайные, то <x>, и абсолютная погрешность 
– тоже случайная величина. Наличие случайных чисел требует введения законов математической статистики. При большом числе измерений отклонения измеряемой величины от истинного значения с противоположными знаками равновероятны, а малые погрешности обладают большей вероятностью появления, чем большие. Распределение ошибок по интервалам отклонений от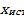 
задается плотностью вероятности 
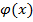, которая определяется распределением Гаусса:
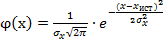(2)
где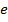 
– основание натуральных логарифмов, 
– дисперсия случайной величины,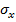 
– ее среднеквадратичное отклонение. Вероятность обнаружения результата измерений в интервале от x до x + dx выражается как dp = 
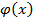dx.
|
|
|
Дисперсия случайной величины характеризует разброс ее значений.
В статистике доказывается, что лучшей оценкой среднего значения дисперсии среднего значения <x> является дисперсия результатов измерений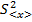 
, которая при ограниченном числе измерений определяется соотношением
. (3)
- среднеквадратичное отклонение среднего значения от истинного значения, или стандартная среднеквадратичная ошибка. Может использоваться для записи конечного результата измерений в виде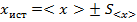 
.
Для небольшого количества измерений в лабораторном практикуме применяется распределение Стьюдента. При количестве измерений n < 10 для повышения надежности вводится добавочный коэффициент Стьюдента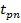 
:
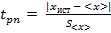. (4)
Его значение зависит от количества измерений n, заданного значения доверительной вероятности p и находится по таблицам. После его нахождения доверительный интервал записывается как 
, это означает, что истинное значение не выходит за границы интервала от 
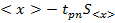до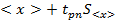 
при предварительно заданно доверительной вероятности. При повышении доверительной вероятности возрастает соответствующий доверительный интервал.
При наличии в результатах измерений, кроме случайных, других видов ошибок, их необходимо также учитывать. В этом случае дисперсию измерений находят по формуле:
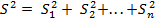, где S1, S2 и т.д. – дисперсия разных видов ошибок. Если одна из дисперсий отличается от других в 2 и более раз, то дисперсию измерений можно принять равной большей из них.
|
|
|
