 |
Обработка результатов косвенных измерений
|
|
|
|
Для измерений, вычисляющихся из прямых можно применять такую же методику, как и для прямых измерений. Вычисляя 
находят среднее значение < 
> и дисперсию средних значений косвенных измерений 
, затем записывают доверительный интервал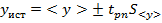 
. Однако, для большого количества измерений этот способ затруднителен, поэтому среднее значение < > получают путем подстановки в функцию среднего значения 
для прямых измерений.
Ход выполнения работы
Измерение длины математического маятника
(прямое измерение)
1. Измерить 10 раз длину нити математического маятника от точки подвеса до центра шарика и занести данные в таблицу:
Результаты измерения длины маятника 1
| N | Σ | ||||||||||
| li, м | 0,338 | 0,343 | 0,340 | 0,340 | 0,342 | 0,338 | 0,340 | 0,340 | 0,340 | 0,342 | 3,403 |
| (li - <l>) 2, м | 0,00000529 | 0,000007 | 0,00000009 | 0,00000009 | 0,00000289 | 0,00000529 | 0,00000009 | 0,00000009 | 0,00000009 | 0,00000289 | 0,00002336 |
2. Найти среднее значение измерений длины по формуле:
(5)
3. Найти среднеквадратичное отклонение длины маятника, обусловленное случайными ошибками по формуле:
(6)
где 
– реальное значение коэффициента Стьюдента для количества измерений n = 10 при надежности 95%.
4. Вычислить среднеквадратичное отклонение, вызванное ошибкой прибора по формуле:
(7)
где f – цена деления измерительного прибора, и 
– значение коэффициента Стьюдента для бесконечного числа измерений при надежности 95%.
5. При сравнимых значениях величин 
и 
среднеквадратичное отклонение 
значения абсолютной ошибки (
) вычисляется по формуле:
(8)
Если одна из ошибок отличается от другой более, чем в 2 раза, то в качестве можно принять большую из них.
|
|
|
Результаты измерений записывают в виде 
.
Определение периода колебаний математического маятника
(прямое измерение)
1. Отклонить маятник от положения равновесия на 5-8̊, измерить время двадцати колебаний 
и подсчитать период колебаний по формуле 
. Провести 10 таких измерений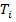 
и результат занести в таблицу:
Результаты измерения периода колебаний 1
| N | Σ | ||||||||||
| Ti, c | 1,12 | 1,13 | 1,18 | 1,135 | 1,14 | 1,16 | 1,16 | 1,17 | 1,165 | 1,115 | 11,475 |
| (Ti-<T>)2,c | 0,00075625 | 0,00030625 | 0,00105625 | 0,00015625 | 0,00005625 | 0,00015625 | 0,00015625 | 0,00050625 | 0,00030625 | 0,00105625 |
2. Повторить все вычисления из определения длины маятника и записать значение периода в виде 
.
3. На измерение периода также значительно влияет скорость реакции измеряющего, поэтому необходимо ее также измерить и занести в таблицу для последующих вычислений. Производится при помощи обычной линейки, которую необходимо держать одной рукой, а вторую поместить на уровне 0; затем линейка отпускается и тут же ловится второй рукой. Отметка, на которой линейка была поймана, отражает пройденный путь. Формула зависимости пройденного пути свободно падающего тела от времени: 
, соответственновремя, за которое линейка проходит путь и будет временем реакции измеряющего: 
.
3.1 Вычисляем ускорение свободного падения для широты и высоты над уровнем моря для г. Ижевска по формуле:
,
где φ – географическая широта = 56̊ 52’ 2” = 56,87 ̊, h – высота над уровнем моря = 160м.
;
;
;
.
=
= 
= 9,8161542061391122846 = 9,816154 м/с2.
Проводим измерения 10 раз и заносим данные в таблицу, обозначив время реакции за B,
B = 
.
| N | Σ | ||||||||||
| Bi,c | 0,225691 | 0,206849 | 0,214109 | 0,201864 | 0,238848 | 0,186109 | 0,199324 | 0,206849 | 0,183352 | 0,201864 | 2,064858 |
| (Bi-<B>)2,c | 0,00036883970704 | 0,000000131 | 0,000058110 | 0,000021363 | 0,001047341 | 0,000415208 | 0,000051285 | 0,000000131 | 0,000535182 | 0,000021363 |
| Результаты измерения времени реакции 1 |
Определение ускорения свободного падения
|
|
|
(косвенное измерение)
1. Использовать полученные данные прямых измерений длины и периода колебаний маятника и вычислить среднее значение ускорения свободного падения по формуле:
(9)
2. Вычислить дисперсию ускорения свободного падения по формуле:
(10)
3. Найти среднеквадратичное отклонение среднего значения ускорения свободного падения по формуле:
(11)
4. Результат измерения ускорения записать в виде 
,
p = 0,95
Вычисления
Единица измерения длины – метр, времени – секунда. Точность вычислений – 6 знаков после запятой.
|
|
|
