 |
Обзор систем компьютерной математики.
|
|
|
|
(1) Универсальная СКМ:1)Maxima-это свободное ПО существует под лицензией GNU GPL, является потомком системы Macsyma, разработанная в начале 60-ых годов 20 века в Массо Чукетском институте (MIT). 2) Axiom-свободная СКМ, разрабатываемая с 1971 года группой исследователей IBM. В 90-ых годах система была продана другой компании-NAG и стала коммерческим продуктом. 3) Reduce-свободная система для научных алгебраических вычислении. 4) Maple- плотная система, продукт компании Watcrloo. Maple предназначена для символьных вычислений и для численного решения, обладает разными графическими системами. 5)Mathematica-платная СКМ компании WolframResearch. Для символьных преобразований и численных расчетов. Поддерживает работу и с графиком и со звуком. 6)MuPAD-СКМ разработанная в германии. Разработанная в 1990 годах. Система имеет собственное ядросимвольной математики. Имеет язык системы, имеет синтаксис схожий с синтаксисом языка Pascal, имеет как свободные распространенные версии, так и коммерческие.
(2)Алгебраические СКМ. 1) GAP-это свободно распространенная СКМ для решения задач вычислительной теории групп. (3)Теория вероятности и мат. статистики. 1)PATISTICA-платный пакет для статистического анализа разработанная компанией statsoft. 2)R-язык программирования для статистической обработки данных и работы с графикой, а также свободная программная среда вычислений с открытыми исходными кодами в рамках проекта GNU.(4) Для численных расчетов. 1)Численные методы. Octave-свободнаясистема для математических вычислений, исполняют совместно с MatLat системы высокого уровня.2) Scthat-свободный пакет прикладных математических программ для инженерии и научных расчетов. С 1994 года распространена вместе с исходным кодом через интернет. 3) Mathhat-платный пакет программирования для решения задач технических вычислений. Имеет свободные коды программирования.
|
|
|
20.Операции с матрицами
Эффект от различных операций с матрицами и векторами будет проще понять, используя символы. Будем использовать две матрицы и два вектора:

Транспонирование
Оператор транспонирования находится на вкладке Математика –> Операторы –> Векторы и матрицы:
Поэлементные операции
Часто операции в векторами приходится совершать поэлементно. Для этого служит оператор векторизации. Операции в Excel зачастую являются поэлементными, они также важны и в Mathcad. Чтобы перемножить два вектора поэлементно, сначала введите простое умножение:
Затем выберите все выражение и примените векторизацию:
Сложение и вычитание
Сложение и вычитание выполняется поэлементно:
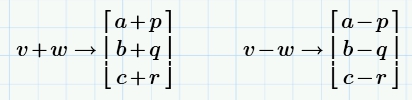
Скалярное произведение
Умножение на константу работает так:

При скалярном умножении матриц происходит умножение строк на столбцы. При этом используется тот же символ, что и при обычном умножении. Эта операция допустима только для тех матриц, в которых число строк в первой матрице равно числе столбцов во второй. Для наших матриц 2х2:

Заметьте, что последовательность множителей играет роль:

Скалярное произведение не коммутативно, за исключением особых случаев:

Векторное произведение
Этот оператор применим только для двух вектор-столбцов, состоящих из трех элементов:
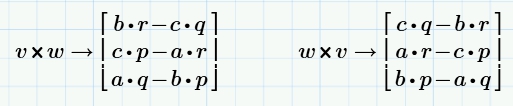
Обратная матрица
Обратная матрица определяется только для квадратных матриц. Произведение матрицы и ее обратной матрицы является единичной матрицей: Произведение матрицы и единичной матрицы дает изначальную матрицу:
Определитель
Определитель можно найти только для квадратной матрицы. Его значение может быть равно нулю, даже если все элементы матрицы не равны нулю. Обратная матрица содержит дроби, в знаменателе которых находится определитель:
|
|
|
Для вектора команда Определитель вычисляет длину вектора:
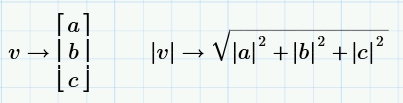
22.
Первоначально рассмотрим СЛАУ в Mathcad. Для их решения может использоваться блок given …find() или специальная функция lsolve(). Применение блока given …find() предопределяет необходимость задания начальных значений искомых переменных. Далее после ключевого слова given описывается СЛАУ и с помощью find() находится решение. Следует указать, что в том случае, когда СЛАУ в Mathcad имеет бесконечное множество решений блок given …find() дает конкретный результат, что несомненно следует отнести к недостаткам. В случае отсутствия решения будет выдано сообщение “ Matrix is singular. Cannot compute its inversу – Матрица сингулярная. Нельзя вычислить эту инверсию ”.
Применение функции lsolve() позволяет избежать этого недостатка. Функция lsolve(M,b) имеет два аргумента. M – матрица коэффициентов при неизвестных, b – вектор свободных членов. На листинге приведен пример решения СЛАУ.
Пример решения СЛАУ:

24.
Для решения системы нелинейных уравнений используются два блока: given…find() и given…minerr (). Так как система нелинейных уравнений может иметь несколько решений, то полученные результаты зависят от начальных значений искомых переменных. В обоих случаях получаются приближенные решения, для которых рекомендуется делать проверку. Обычно в Mathcad требуется, чтобы количество уравнений было равно количеству искомых переменных, но в некоторых случаях, когда с точки зрения классической математики может быть получено точное решение и при меньшем количестве уравнений, данное условие может быть нарушено. На листинге представлены примеры использования блоков given…find() и given…minerr () для решения систем нелинейных уравнений.

|
|
|


