 |
Терморезистивные преобразователи
|
|
|
|
- Цель и содержание работы
Работа предназначена для ознакомления студентов с проволочными и полупроводниковыми терморезисторами, используемыми в качестве термометров сопротивления.
Содержанием работы является градуировка двух типов термометров сопротивления в диапазоне температур 0 ÷ 100ºС и расчет их основных характеристик.
- Принцип действия и устройство терморезисторов
Измерение температуры термометрами основано на свойстве электрических проводников менять сопротивление в зависимости от температуры. Зная зависимость R = f(t) можно по величине сопротивления R определить температуру t, до которой нагревает термометр сопротивления.
Основным материалом для чувствительных элементов терморезисторов являются чистые металлы и ряд полупроводников. Большинство химически чистых металлов обладает положительным температурным коэффициентом сопротивления, колеблющимся (в интервале 0 ÷ 100ºС) от 0,35 до 0,68% на 1ºС. Наибольшее распространение для изготовления чувствительных элементов имеют медь, платина и никель.
Зависимость сопротивления металлов от температуры, как правило, не является линейной. Для платины зависимость сопротивления R от температуры t в пределах от 0 до +660ºС выражается уравнением:
 , (1)
, (1)
где 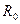 - сопротивление при 0ºС.
- сопротивление при 0ºС.
Для чистой платины:  ,
,  .
.
В интервале от 0 до -190 ºС зависимость сопротивления платины от температуры выражается уравнением:
 , (2)
, (2)
где  .
.
Для меди в интервале -50 ÷ (-200) ºС при сопротивлении, соответствующей температуре t, пользуются обычно формулой:
 , (3)
, (3)
где 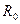 - сопротивление при температуре t0;
- сопротивление при температуре t0;
 - температурный коэффициент для интервала температур, начинающегося от t0.
- температурный коэффициент для интервала температур, начинающегося от t0.
|
|
|
Формула (3) выражает линейную зависимость сопротивления от температуры.
Следует отметить, что сопротивление 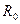 в формуле (3) должно соответствовать начальной температуре того интервала температур, для которого задано значение
в формуле (3) должно соответствовать начальной температуре того интервала температур, для которого задано значение  .
.
Действительно, пусть  задано для интервала температур от t0 до tк (рис.1).
задано для интервала температур от t0 до tк (рис.1).
Тогда R = f(t) представляет собой участок прямой АВ между абсциссами 1 и 2.
Для температуры t внутри рассматриваемого участка справедливо:
 . (4)
. (4)

Рис.1. Вид градуировочной характеристики проволочного термометра сопротивления.

Рис.2. Вид градуировочной характеристики полупроводникового термометра сопротивления.
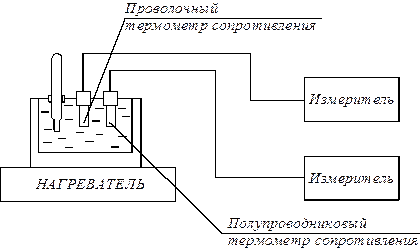
Рис.3. Блок-схема экспериментальной установки.
При сравнении формул (4) и (3) видно, что:
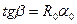 и
и  . (5)
. (5)
Величина  имеет физический смысл, характеризуя чувствительность термометра сопротивления. В самом деле, чувствительность терморезистора представляет собой отношение изменения сопротивления к соответствующему изменению температуры. Если обозначить чувствительность термометра сопротивления через
имеет физический смысл, характеризуя чувствительность термометра сопротивления. В самом деле, чувствительность терморезистора представляет собой отношение изменения сопротивления к соответствующему изменению температуры. Если обозначить чувствительность термометра сопротивления через 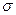 , то
, то
 ,
,
В простейшем случае линейной зависимости R = f(t) легко видеть, что
 .
.
Таким образом, чувствительность термометра сопротивления определяется величиной 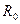 , а также чувствительностью термометрического материала
, а также чувствительностью термометрического материала  , из которого выполнен его чувствительный элемент.
, из которого выполнен его чувствительный элемент.
В качестве чувствительных элементов терморезисторов, благодаря высоким температурным коэффициентам и малым размерам при значительном сопротивлении, все большее применение находят полупроводниковые термосопротивления.
Основной характеристикой термосопротивления считается температурная зависимость, определяемая в рабочем диапазоне температур выражением:
 , (6)
, (6)
где 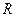 - величина термосопротивления, соответствующая температуре
- величина термосопротивления, соответствующая температуре 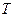 ;
;
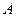 и
и  - постоянные коэффициенты, характеризующие свойства материала и геометрию термосопротивления.
- постоянные коэффициенты, характеризующие свойства материала и геометрию термосопротивления.
|
|
|
Выражение (6) можно представить в виде:
 , (7)
, (7)
где 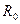 соответствует
соответствует  .
.
Согласно определению и выражениям (6) и (7) температурный коэффициент определяется как
 . (8)
. (8)
Следовательно, температурный коэффициент зависит от температуры и характеризует термосопротивление лишь в определенной точке.
Тогда на основании уравнений (7) и (8) можно записать:
 , (9)
, (9)
где  и
и 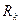 соответствует
соответствует  .
.
Температурный коэффициент термосопротивления можно определить на основании его температурной характеристики.
Для температур  и
и 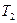 имеем:
имеем:
 и
и 
 . (10)
. (10)
Откуда  . (11)
. (11)
Температурный коэффициент сопротивления определится по формуле:
 . (12)
. (12)
Задача может быть решена и графически. Предположим, что необходимо определить  при температуре
при температуре 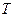 , что соответствует точке А на кривой R = f(t) (рис.2), тогда
, что соответствует точке А на кривой R = f(t) (рис.2), тогда
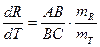 ,
,
Искомая величина температурного коэффициента будет равна:
 , (13)
, (13)
где  - масштаб оси ординат, Ом/мм;
- масштаб оси ординат, Ом/мм;
 - масштаб оси абсцисс, К/мм.
- масштаб оси абсцисс, К/мм.
Чувствительность полупроводникового термометра сопротивления при температуре 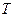 определяется как величина
определяется как величина
 (14)
(14)
или
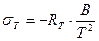 . (15)
. (15)
- Методика выполнения работы и описание экспериментальной установки.
Работа выполняется с одним проволочным и одним полупроводниковым термометрами сопротивления. Нагрев этих двух терморезисторов производится в специальном сосуде. Измерение их сопротивления проводится с помощью универсальных цифровых приборов. Схема экспериментальной установки приведена на рис.3.
При градуировке термометров сопротивления их температура меняется от 0 до +100ºС. Сопротивление проволочного термометра измеряется через каждые 10º, а полупроводникового – через 5º в диапазоне температур 0…-30ºС и через 10º в диапазоне +30… +100ºС.
- Порядок выполнения работы
- Поместить исследуемые термометры сопротивления в сосуд с тающим льдом, выдержать их до установления температурного равновесия между чувствительными элементами и окружающей средой и измерить сопротивление
 .
. - Включить нагреватели и произвести градуировку термометров сопротивления в диапазоне 0 ÷ (+100)ºС. Измерение сопротивления выполнять согласно указания раздела 3. Результаты эксперимента занести в таблицу.
- Построить градуировочную характеристику R = f(t) для проволочного термометра сопротивления.
- Определить чувствительность проволочного терморезистора
 . Значение
. Значение  находится по градуировочной кривой (см. рис.1).
находится по градуировочной кривой (см. рис.1). - Определить величину коэффициента
 для диапазона температур 0 ÷ 100ºС по формуле (5).
для диапазона температур 0 ÷ 100ºС по формуле (5). - Построить градуировочные характеристики R = f(t) для полупроводникового термометра сопротивления.
- Рассчитать величину коэффициентов В по формуле (11) для полупроводникового терморезистора. Значения температур Т1 и Т2 указывается преподавателем.
- Определить температурный коэффициент полупроводникового терморезистора по формуле (13) для среднего значения температуры в интервале Т1 ÷ Т2.
- Для этой же температуры найти чувствительность полупроводникового терморезистора графическим путем по градуировочным характеристикам и формуле (14) и расчетным путем по формуле (15).
|
|
|
- Содержание отчета
В отчет должны быть включены:
- Таблицы с результатами эксперимента.
- Графики градуировочных характеристик.
- Расчеты значений температурных коэффициентов и чувствительности.
ЛАБОРАТОРНАЯ РАБОТА № 23
|
|
|


