Количественные теории информации. Мера Шеннона

Содержание

Введение............................................................................................................................................................................. 2

Кобщему определению понятия информации............................................................................... 3

Количественные теории информации. Мера Шеннона................................................................................ 3

Качественный аспект информации....................................................................................................................... 4

Информация как функция разнообразия.............................................................................................................. 6

Отражение и информация........................................................................................................................................... 7

Информация и сложные системы.............................................................................................................. 9

К определению понятия системы........................................................................................................................... 9

Информация в кибернетических системах...................................................................................................... 11

Информация в теоретико-игровых моделях.................................................................................................... 13

Связь информации с законами и категориями диалектики............................................. 14

Законы диалектики и информация...................................................................................................................... 14

Информация и развитие............................................................................................................................................. 15

Информация, законы природы и причинность................................................................................................ 16

Пространство-время и информация..................................................................................................................... 18

Информация и общество................................................................................................................................... 19

Особенности социальной информации............................................................................................................. 19

Научно-техническая информация и познание.............................................................................................. 21

Общество и информатизация.................................................................................................................................. 22

Заключение................................................................................................................................................................... 25

Литература..................................................................................................................................................................... 25

Введение

Теория информации — одна из наиболее бурно развивающихся отраслей современного научного знания. За полвека с момента возникновения она насчитывает почти столько же работ, сколько и теория относительности — один из фундаментальных разделов современной физики. В настоящее время формула количества информации К. Шеннона, наверное, известна не менее, чем формула взаимосвязи массы и энергии А. Эйнштейна. К тому же если теория относительности применяется только физиками, то теория информации проникает во многие науки о живой и неживой природе, обществе и познании, ее используют и физики, и биологи, и экономисты, и ученые многих других специальностей.

Теория информации нужна не только науке, но и производству. Современное производство стало очень сложным; в связи с этим на первый план в нем выдвигаются вопросы организации и управления, основанные на процессах передачи и преобразования информации. Без изучения и широкого использования информации было бы чрезвычайно затруднено дальнейшее преобразование вещества и энергии в процессе производства. Кроме того, совсем недавно появился и в настоящее время бурно развивается принципиально новый сектор производства — производство не вещественно-энергетических, а чисто информационных товаров.

Естественно, что интенсивное развитие теории информации и ее приложений ставит ряд вопросов философского характера. И прежде всего возникает проблема выявления содержания самого понятия «информация». При анализе этого понятия мы вынуждены вовлекать в рассмотрение материальный субстрат, на котором развертываются процессы движения информации — информационные системы. Поэтому в обзор философской теории информации входит как неотъемлемая часть изложение основных положений философской теории систем.

Структура изложения такова. Сначала описан ряд частных теорий информации, обладающих весьма ограниченной областью применения, но дающих хорошие результаты для определенных классов явлений. Каждая из этих теорий сама по себе связана с теми или иными философскими обобщениями и потому их рассмотрение имеет непосредственное отношение к теме реферата. Далее раскрывается связь понятия информации с философскими категориями различия и отражения. Определение информации, получаемое на этом пути, принимается в качестве наиболее общего и используется всюду в оставшейся части.

Второй раздел посвящен системам и информационным процессам в них. Дано общее определение системы и уточнены отдельные аспекты этого понятия. Отдельно рассмотрен класс систем, имеющий особую важность, — сложные самоуправляемые (кибернетические) системы.

В третьем разделе описана связь понятия информации с законами и категориями диалектики. Особое внимание уделено категориям причинности, пространства, времени и развития.

Наиболее сложным из известных систем являются человеческое общество. Чрезвычайно сложны и информационные процессы, протекающие в нем. В последнем разделе рассматривается социальная информация вообще и такой особый вид ее, как научная информация. Наконец, сказано о некоторых проблемах, специфических для современного общества и связанных с бурным развитием устройств обработки информации.

Кобщему определению понятия информации

Количественные теории информации. Мера Шеннона

До эпохи интенсивного развития систем связи и до возникновения кибернетики понятие информации считалось интуитивно понятным и не нуждающимся в точных определениях, а тем более в философском анализе. История учений об информации начиналась с разработки ее количественного аспекта, что диктовалось потребностями радио- и телефонной связи. При этом любая количественная теория неизбежно была связана с попыткой дать то или иное общее определение. Каждой формуле количества информации соответствовал свой взгляд на ее сущность.

Наиболее разработанной является статистическая теория информации [А11], [Б11], возникшая на базе теоретико-вероятностных подходов и связанная с определением информации как снятой неопределенности.

В задачах теории связи рассматривается система, состоящая из источника информации, приемника и расположенного между ними канала связи. Существенно, что для получателя единственным способом получения информации является считывание сообщения из канала связи. Иными словами, приемная сторона не может достоверно предугадать следующее сообщение. Так в рассмотрение вводится понятие неопределенности, играющее в теории фундаментальную роль. До приема сообщения у приемника существует неопределенность (незнание) относительно того, какое сообщение придет следующим. Акт приема сообщения снимает данную неопределенность. Если известно, что в канале всязи отсутствуют помехи, то неопределенность снимается полностью. В противном случае неопределенность устраняется лишь частично, так как у приемной стороны остается еще неопределенность (сомнение) относительно того, не является ли принятое сообщение результатом искажения.

Таким образом, неопределенность, снимаемая в результате приема сообщения, отождествляется с информацией. Такое определение весьма близко к житейскому пониманию: информацией мы, как правило, склонны считать то, что для нас еще не известно, ново, то, что уменьшает наше незнание. Например, пусть нас интересует вопрос, прибыл ли поезд. При этом у нас нет никаких оснований для предположения, что он действительно прибыл, так же как и для противоположного предположения. Равновероятность этих двух возможностей означает максимальную неопределенность выбора. Позвонив на вокзал по телефону, и получив ответ на интересующий нас вопрос, мы тем самым устраним неопределенность до нуля. Заметим, что как положительный, так и отрицательный ответ (ввиду их равновероятности) устраняют неопределенность в равной мере. Устранение неопределенности выбора из двух равновероятных возможностей соответствует одному биту информации.

Рассмотрим теперь другую ситуацию, аналогичную первой во всем, кроме того, что мы заранее на 90% уверены в том, что поезд еще не пришел, и лишь 10% оставляем на долю сомнения. Получив по телефону ответ «поезд не пришел», мы не узнаем почти ничего нового: мы и так были заранее подготовлены к такому исходу. Поэтому есть основание считать, что получено мене 1 бита информации. Напротив, получив неожиданный ответ, то есть ответ с большей неопределенностью, мы получаем более 1 бита информации.

Количественным выражением неформального понятия «неопределенность» служит известная и с успехом применяемая мера Шеннона. Пусть всего возможны 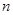 типов сообщений, причем для каждого типа сообщения  априори известна его вероятность . Неопределенность отдельного типа сообщения выражается формулой . Эта формула полностью удовлетворяет рассмотренному выше требованию, так как для более вероятных событий, , она дает малую неопределенность  и, наоборот, для маловероятных событий (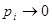) получаем возрастающую неопределенность 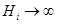. В частности, событие, которое с полной достоверностью может быть предсказано заранее () не несет никакой информации ().

Теперь для определения средней неопределенности одного акта приема сообщения нужно лишь усреднить индивидуальные неопределенности  по множеству типов сообщений:

Формула Шеннона совпадает по виду с формулой Больцмана для статистического определения энтропии, взятой с обратным знаком [А2]. В термодинамике энтропия служит мерой хаотичности, беспорядка в системе. Таким образом, информация, будучи отрицательной энтропией (негэнтропией) может рассматриваться как вклад в упорядочение системы.

Развитие статистической теории информации привело к следующим результатам. Во-первых, стало возможным строгое количественное исследование информационных процессов. Во-вторых, был расширен объем понятия информации, так как статистическая теория полностью отвлекается от двух высших семиотических аспектов информации: семантичиского (смыслового) и прагматического (ценностного). С позиций этой теории информацию несет не только человеческая речь, но и любые объекты и процессы, которые подчиняются статистическим закономерностям.

Далее, статистический подход позволил выявить фундаментальную связь информационных процессов и термодинамики. Знак «минус» в формуле Шеннона однозначно указывает на то, что информационные процессы в известном смысле противоположны естественным термодинамическим процессам, ведущим, как известно, к деградации. Статистическая теория прямо связывает информацию с процессом превращения возможности в действительность, случайности в необходимость, что уже дает основание для философского анализа. Наконец, в рамках статистического подхода было получено первое определение информации, удовлетворительное с философской точки зрения: информация есть устраненная неопределеность.

Вместе с тем, статистическая теория обладает и существенными недостатками, которые являются продолжением ее достоинств. Во-первых, информация связывается лишь со случайными процессами, подчиняющимися вероятностным законам. Статистическая теория утверждает, что информационные процессы не происходят в однозначно детерминиованных системах. В частности, компьютер, выполняющий определенную программу и функционирующий по законам необходимости, оказывается, согласно статистической теории, неинформационной системой, а игральная кость — информационной. Во-вторых, отвлечение от осмысленности и полезности информации, вполне уместное при анализе систем связи, уже не может нас удовлетворить, если речь идет о живых системах, о человеке и обществе. Эти и другие неадекватности заставляют искать иные, более общие определения информации. Это, конечно, означает не отказ от статистической теории, а лишь четкое определение области ее применимости.

Характерной особенностью статистической теории является то, что в качестве математического средства формализации понятия неопределенности была выбрана вероятность. Однако понятие неопределенности в общем случае оказывается шире понятия вероятности, а статистическая теория не может правильно описывать те процессы снятия неопределенности, которые к вероятности не сводятся. Действительно, пусть имеется множество элементов, из которых осуществляется выбор. Выбор может происходить и по заранее заданному закону (детерминированному алгоритму), неизвестному познающему субъекту. В этом случае у субъекта существует неопределенность относительно данного закона, однако эта неопределенность имеет невероятностную природу. Даже если к такому случаю удастся применить статистическую теорию, это будет искусственный прием, искажающий внутреннюю логику и сущность познаваемого процесса. Это есть ни что иное, как втискивание реальной ситуации в прокрустово ложе готовой теории вместо того, чтобы разработать теорию, адекватную своему предмету.

Невероятностные теории, относящиеся к качественному аспекту информации, будут рассмотрены ниже. Здесь же упомянем одну из наиболее известных невероятностных количественных теорий — алгоритмический подход А. Н. Колмогорова. В основе подхода лежит тот факт, что количество информации, заключенной в объекте  нас чаще всего интересует не само по себе (абсолютное количество информации), а относительно определенного объекта 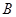, то есть взаимное, относительное количество информации. Количество информации по А. Н. Колмогорову — это сложность объекта  относительно объекта 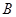, данного в качестве строительного материала. А именно, количество информации измеряется как наименьшая длина алгоритма, строящего объект  из объекта 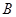. Алгоритмический подход связан с конструктивным направлением в математике.

Предыдущая1234567891011Следующая

Поделиться:

Воспользуйтесь поиском по сайту: