Принятие решений в условиях неопределенности.

 

При принятии решений в условиях неопределенности, ког­да вероятности возможных вариантов обстановки неизвестны, могут быть использованы ряд критериев, выбор каждого из ко­торых, наряду с характером решаемой задачи, поставленных целевых установок и ограничений, зависит также от склонности к риску лиц, принимающих решения.

К числу классических критериев, которые используются при принятии решений в условиях неопределенности, можно отнести:

Критерий обобщенного максимина (пессимизма — оптимизма) Гурвица используется, если требуется остановиться между линией поведения в расчете на худшее и линией поведения в рас­чете на лучшее.

В этом случае предпочтение отдается варианту решений, для которого окажется максимальным показатель С, определяемый из выражения:

                                                      j                         j

где k  — коэффициент, рассматриваемый как показатель оп­тимизма ,

при к = 0 — линия поведения в расчете на лучшее, при к = 1 — в расчете на худшее;

 — выигрыш, соответствующий і-му решению при j-м ва­рианте обстановки.

Нетрудно убедиться, что при к = 1 критерий Гурвица совпа­дает с критерием Вальда, т.е. ориентация на осторожное пове­дение. При к = 0 — ориентация на предельный риск, т.к. боль­шой выигрыш, как правило, сопряжен с большим риском. Зна­чения k между 0 и 1 являются промежуточными между риском и осторожностью и выбираются в зависимости от конкретной об­становки и склонности к риску лица, принимающего решение.

В таблице 5.6 приведены значения показателя G для различ­ных вариантов решений в зависимости от величины коэффици­ента k.

Таблица

Значение показателя G для различных k

Решение	Значение коэффициента k
	0,00	0,25	0,50	0,75	1,00
P1	0,400	0,362	0,325	0,287	0,250
P2	0,750	0,612	0,475	0,337	0,200
P3	0,820	0,640	0,460	0,280	0,100
P4	0,800	0,650	0,500	0,350	0,200
Оптимальное решение	P1	P2	P3	P4	P1

 

Как видим, с изменением коэффициента k изменяется вари­ант решения, которому следует отдать предпочтение.

Нами рассмотрены наиболее общие (классические) методы, которые позволяют обосновывать и принимать решение при нео­пределенности экономических данных и ситуаций, недостатке фактической информации об окружающей среде и перспектив­ных ее изменений.

Следует отметить, что разработанные экономической тео­рией и практикой, способы и приемы решения задач в условиях риска и неопределенности не ограничиваются перечисленными методами. В зависимости от конкретной ситуации в процессе анализа используются и другие методы, способствующие реше­нию задач, связанных с минимизацией риска.

Практическая часть

 

Вариант 1

 

 

4.2.1 На основании выборочных данных о длительности телефонных разговоров, количестве разговоров, а также средней стоимости одной минуты разговора, принимая, что длительность разговора подчиняется нормальному закону распределения, определить:

- ожидаемые доходы по городским разговорам;

- размер доходов, который может быть получен с вероятностью 68% и 99,7%

 

 

Исходные данные:

 

Длительность телефонных разговоров

 

Длительность разговоров (минут)	1	2	3	4	5	6	7
Частота появления	32	72	152	232	212	122	42

 

Количество разговоров – 2200 тыс.ед.

Средняя стоимость одной минуты разговора – 0,4 грн.

 

Для ограниченного числа возможных значений случайной величины ее среднее значение определяется по формуле:

 

 

-объем выработки (число наблюдений)

- значение случайной величины

- вероятность появления случайной величины

 

Необходимо рассчитать объем выборки:

 

 

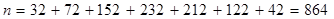
Рассчитываем вероятность появления случайной величины по формуле:

 

 

И заносим в таблицу:

 

Длительность разговоров (минут)	1	2	3	4	5	6	7
Частота появления  ()	32	72	152	232	212	122	42
Вероятность появления ()	0,037	0,083	0,176	0,269	0,245	0,141	0,049

 

Средняя величина, представляющая собой обобщенную характеристику ожидаемого результата, т.е. средняя длительность разговора составит:

 

мин.

 

 

Ожидаемые доходы составят:

 

4,221 х 2200000 х 0,4 = 3714480 грн.

 

Рассчитываем дисперсию (средневзвешенное отклонение) по формуле:

 

 

Среднеквадратическое отклонение:

 

Рассчитываем коэф-т вариации, который показывает степень отклонения полученных значений:

 

Размер доходов с вероятностью 68%

 

(4,221 + 1,429) х 2200000 х 0,4 = 4972000

(4,221 - 1,429) х 2200000 х 0,4 = 2456960

 

С вероятностью 68% доходы могут быть получены в пределах от 2456960 грн. до 4972000 грн.

 

Размер доходов с вероятностью 99,7%

(4,221 + 3 х 1,429) х 2200000 х 0,4 = 7487040

(4,221 - 3 х 1,429) х 2200000 х 0,4 = -58080

 

С вероятностью 99,7% доходы могут быть получены в пределах от -58080 грн. до 7487040 грн.

4.2.2 По исходным данным об эффективности проектов А и В о доходах и соответствующих им значениям вероятности, оценить меру риска и выбрать проект, который обеспечивает наименьшую величину риска.

 

Исходные данные:

 

Оценка возможного результата	Проект А		Проект В
	Доходы	Вероятность	Доходы	Вероятность
Пессимистическая	305	0,2	240	0,25
Наиболее вероятная	1005	0,6	900	0,5
Оптимистическая	1505	0,2	1800	0,25

 

Выполним задачу с использованием двух критериев:

- средневзвешенная оценка риска использующая выражение

- методом , использующие для оценки риска среднее значение отдачи и ее среднеквадратическое отклонение.

 

Величина потерь по вариантам:

 

Пессимистическая оценка:

Проект А - 305-305=0

Проект В - 305-240=65

 

Вероятная оценка:

Проект А – 1005-1005=0

Проект В – 1005 -900=105

 

Оптимистичная оценка:

Проект А – 1800-1505=295

Проект В – 1800-1800=0

 

Проект	Ситуация
	Пессимистическая	Вероятная	Оптимистичная
Проект А	0	0	295
Проект В	65	105	0

 

Тогда средневзвешенный показатель риска по вариантам составит:

 

Вариант В – менее рискованный, а следовательно эффективней.

 

Среднее значение отдачи:

 

Дисперсия:

 

Среднеквадратическое отклонение:

 

По проекту А отдача больше Ии он  явл. менее рискрванным, т.к

 

Коэффициент вариации:

 

 

По данному показателю, предпочтение следует отдать проекту, у которого коэффициент вариации меньше, а это проект А. Он явл. менее рискованным. Но следует учитывать что использование данного коэффициента в значительном количестве случаев может привести к выбору заведомо худшего варианта.  

Вывод: Следовательно, предпочтение нужно отдать проекту А, как более осторожному. Но проект В может дать большую прибыль.

4.2.3 Известна матрица эффективности решений в зависимости от возможных условий их реализации. Необходимо выбрать наилучший вариант по критериям:

 

- максимин (критерий Вальда);

- минимакс (критерий Севиджа);

- обобщенный максимин(Критерий Гурвица). При коэффициенте оптимизма 

К=0,6.

 

Исходные данные:

 

⇐ Предыдущая1234Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: