ТЕМА 5. Непараметрические методы оценки достоверности результатов статистического исследования. Критерий соответствия (хи-квадрат)

ЦЕЛЬ ЗАНЯТИЯ: Освоить методику вычисления и использования критерия соответствия для определения достоверности расхождения между несколькими сравниваемыми группами изучаемых явлений.

Методика проведения занятия: Студенты самостоятельно готовятся к практическому занятию по рекомендованной литературе и выполняют индивидуальное домашнее задание. Преподаватель в течение 10 минут проверяет правильность выполнения домашнего задания и указывает на допущенные ошибки, проверяет степень подготовки с использованием тестирования и устного опроса. Затем студенты самостоятельно вычисляют критерий соответствия для определения достоверности расхождения между несколькими сравниваемыми группами изучаемых явлений, оценивают полученные данные и формулируют заключение. В конце занятия преподаватель проверяет самостоятельную работу студентов.

КОНТРОЛЬНЫЕ ВОПРОСЫ:

1. Когда применяется показатель соответствия «хи-квадрат»?
2. На чем основан расчет показателя χ²?
3. Что такое «нулевая гипотеза»?
4. Из каких этапов складывается исчисление критерия соответствия «хи-квадрат»?
5. Как определяется число степеней свободы при расчете критерия соответствия?
6. Как оценивается полученный результат показателя соответствия?
7. Когда различия между несколькими сравниваемыми группами оцениваются как существенные?

КРАТКОЕ СОДЕРЖАНИЕ ТЕМЫ:

Непараметрическими являются количественные методы статистической обработки данных, применение которых не требует знания закона распределения изучаемых признаков в совокупности и вычисления их основных параметров.

Описанные выше статистические критерии достоверности (критерий Стьюдента t, критерий Фишера F и др.) относятся к параметрическим, т. к. используют стандартные параметры распределений (М, Р, m, n). Они связаны с законом нормального распределения и применяются для оценки расхождения между генеральными параметрами по выборочным показателям сравниваемых совокупностей. Существенным достоинством параметрических критериев служит их большая статистическая мощность, т. е. широкие разрешающие возможности, а недостатком – трудоемкость расчетов, неприменимость к распределениям, сильно отклоняющимся от нормального, а также при исследовании качественных признаков.

Наряду с параметрическими критериями для ориентировочной оценки расхождений между выборками (особенно небольшими) применяются так называемые непараметрические критерии, что позволяет сравнивать выборки как по количественным, так и по качественным признакам, значения которых не имеют числового представления, но которые можно ранжировать. Конструкции непараметрических критериев отличаются простотой.

В медицине для доказательства некоторого утверждения часто применяют метод, известный в математике как «доказательство от противного». Для этого в качестве рабочего инструмента используют так называемую «нулевую гипотезу». Гипотеза, в соответствии с которой отсутствуют различия между различными совокупностями, называется нулевой гипотезой.

Например, если надо показать, что заболеваемость в целом ниже у лиц, занимающихся физкультурой и спортом, чем у ведущих малоподвижный образ жизни, то выдвинем гипотезу об отсутствии различий в их состоянии здоровья. Затем попробуем отвергнуть эту гипотезу.

«Нулевая гипотеза» широко используется при оценке достоверности различия сравниваемых групп по критерию соответствия (хи-квадрат).

Критерий соответствия χ² применяется для статистической оценки закона распределения эмпирических вариационных рядов и для доказательства достоверности различий между двумя или несколькими выборочными совокупностями. Критерий соответствия применяется, когда результаты исследования представлены абсолютными величинами, и результат исхода имеет много градаций (выздоровел, состояние улучшилось, ухудшилось, умер), а также, если в подлежащем имеется несколько признаков (несколько возрастных групп, несколько методов лечения, кормления и т.д.). Критерий основан на предположении (нулевой гипотезе) об отсутствии разницы между величинами, полученными в результате выборочного наблюдения и теоретически вычисленными. Чем больше фактические величины отличаются от ожидаемых, тем больше уверенность, что изучаемый фактор оказывает существенное влияние.

Вычисляется критерий соответствия по формуле χ² =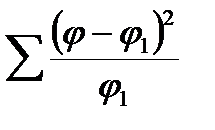

Первым этапом в вычислении критерия соответствия являются формулировка нулевой гипотезы и исчисление ожидаемых величин. При определении ожидаемых чисел рекомендуется для большей точности расчета χ² вычислять их до десятых. На следующем этапе определяется разность между фактическими и ожидаемыми числами по всем группам (φ – φ₁). Затем определяют квадрат разностей (φ – φ₁)² и делят его на ожидаемое число в каждой группе 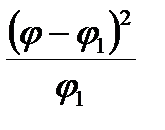. Критерий соответствия определяется путем суммирования всех предыдущих результатов по всем группам. Полученную величину χ² оцениваем по таблице критических значений (приложение 3), для чего определяют число степеней свободы n = (S – 1)(R – 1), где S – число строк, R – число рядов. Нулевая гипотеза подтверждается, если χ² меньше критического (табличного значения), и опровергается, если полученная величина χ² равна или больше табличного значения (приложение, табл. 4).

Пример расчета критерия соответствия (табл. 4).

1 этап – формулируем нулевую гипотезу – введение противогриппозной вакцины не повлияло на заболеваемость гриппом. В этом случае распределение на заболевших и не заболевших в двух группах наблюдения должно быть одинаковым и соответствовать итоговому распределению. Из 94 человек не заболел 61, а из 73 вакцинированных сколько могло быть не заболевших, если бы вакцинация не влияла на заболеваемость?

=47,4

Ожидаемое число заболевших среди вакцинированных будет определяться по пропорции:

= =25,6

Так же вычисляются ожидаемые величины для заболевших и не заболевших гриппом из числа не вакцинированных.

= = 13,6 = = 7,4

Таблица 4