 |
Оценка эффекта факторизации .
|
|
|
|
Этот эффект характеризуется разностью цен схемы до и после факторизации.
Можно показать, что для однократной факторизации ее эффект определяется выражением:
DSQ= SQдо - SQпосле=m(k-1)+q-D,
где m - количество букв, выносимых за скобки;
k - количество термов, из которых происходит вынесение. q - количество термов, в которых после вынесения осталась одна буква (q£k);
D=1, если вынесение осуществляется из всех термов;
D=2, если не из всех.
Для эффективного решения задачи факторизации необходимо учитывать следующий момент:
1) При наличии у булевой функции нескольких минимальных форм целесообразно выбрать из них такие, для которых применение факторизации даст выигрыш в цене схемы.
2) При минимизации не полностью определенной булевой функции может оказаться, что максимальный эффект за счет факторизации дает нормальная форма, не являющаяся минимальной.
Пример:
|10x1 _ _
cmin(f)=|xx10 МДНФ y=x3x4vx1x2x4 SQ=7
|10x1 _ _ _
cmin(f)=|101x ДНФ y= x1x2x4 vx1x2 x3= x1x2(x3v x4) SQ=5
В некоторых случаях максимального эффекта за счет факторизации можно достичь путем расширения термов МНФ с применением законов товтологии
МДНФ y=x1x2x3vx1x2x4vx1x3x5x6vx2x4x5x6= SQ=18
= x1x2(x3v x4)v x5x6(x1x3v x2x4)= SQ=16
= x1x2(x1x3v x2 x4)v x5x6(x1x3v x2x4)= SQ=20
=(x1x3v x2 x4)(x1x2v x5x6) SQ=14
Построение одновыходных схем.
Декомпозиция булевых функций.
Задача декомпозиции булевой функции в общем случае состоит в таком разделении множества ее аргументов на ряд подмножеств, при котором можно выразить исходную функцию f(x) через вспомогательную промежуточную функцию j(z), где zÌx.
В частном случае имеет место так называемая простая разделительная декомпозиция, при которой множество аргументов x разделяется на два непересекающихся подмножества (z,w®(zÇw=j;zÈw=x)) и приведение исходной функции к виду f(x)=f(j(z,w)).
|
|
|
Пример: f3(x)=V(1,2,4,7)
(f=1)
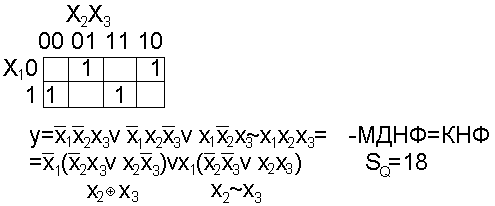
z=(x2x3) W={x1}
_ _
j(z)=x2x3vx2x3
_ _
f(x)=x1j(z)vx1j(z) SQ=13
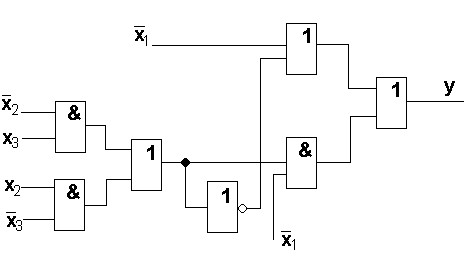
SQ=13 T=5t
Схема базиса Жигалкина.
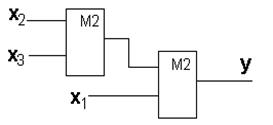
SQ=4 T=2t
Применение декомпозиции там, где он уместно, во многих случаях позволяет уменьшить цену синтезируемой схемы.
_ _ _ _ _ _ _ _ _ _
МДНФ y=x1x2x3x4vx2x5vx3x5vx4x5=x1x2x3x4vx5(x2vx3vx4)
SQ=14
_
j(z)=x2vx3vx4
___ _
f(x)=x1*y(z)vx5*j(z) SQ=10
Синтез многовыходных комбинационных схем.
МКС представляется в виде обобщенного «черного ящика»
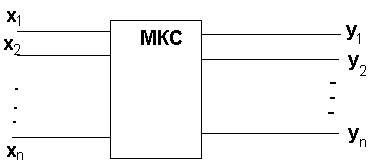
Закон функционирования МКС представляется в виде системы булевых функций
|y1=f1(x1...xn)
|y2=f2
|.
|.
|.
|yn=fn
Естественным образом, при решении задачи синтеза МКС применяются методы факторизации и возможной декомпозиции, применительно не к одной функции, а к системе.
Минимизация системы Булевых функций
Задача минимизации применительно к системе Булевых функций решается аналогично как для одной функции и сводится к получению минимального покрытия. Для решения этой задачи система приводится к одной функции путем дополнения множества агументов подмножеством вспомогательных переменных, с помощью которых выделяются отдельные функции системы. Количество вспомогательных переменных k³log2m, m - количество функций.
Пример:
Раздельная минимизация:
y1 Cmin (y1)= 
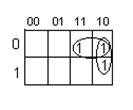
y2 Cmin (y2)= 
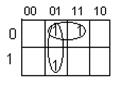
МДНФ: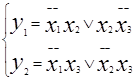 
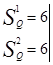
При построении схемы по этому выражению, она разлагается на две независимые подсхемы, отдельные для реализаций каждой функции.
Совместная минимизация
Пусть V=0 для у1; V=1 для y2
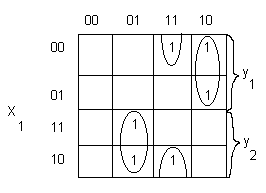Cmin(y1,y2)= 
;
|
|
|
Z=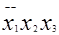 
(общий терм)
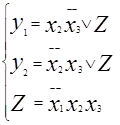
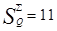
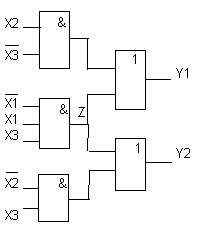
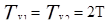
Пример:
V1V2=00 y1
V1V2=01 y2
V1V2=10 y3
V1V2=11 y4
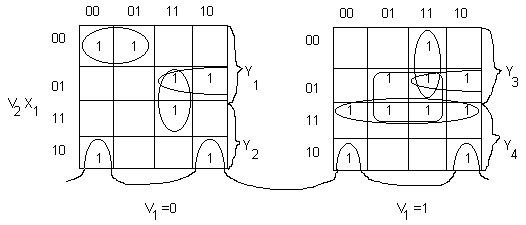
Cmin(S)=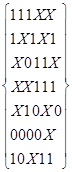 
Общие термы:
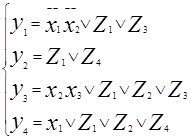
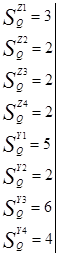
При совместной минимизации Булевых функций система в минимальной форме может оказаться, что некоторые термы поглощаются другими, т.е. после получения минимальной формы необходимо исключить поглощаемые термы.
После получения минимального покрытия при записи минимальных форм с начала выделяются термы, общие для нескольких функций и обозначаются вспомогательными функциями (Z1-Z4).
В целях удобства рядом с каждым общим термом рекоммендуется проставить его принадлежность.
Далее выписываются минимальные формы для отдельных функций с учетом их собственных термов и общих термов, принадлежащих данной функции. При наличии незадействованных комбинаций вспомогательных переменных все наборы аргументов для них являются безразличными.
Пример: 
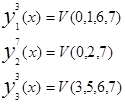
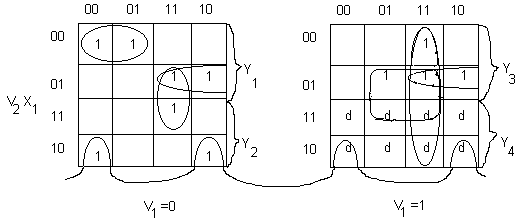
Сmin(S)=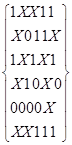 
Для большого числа функций и их аргументов применение карт Карно для совместной минимизации выглядит затруднительным. В этом случае можно использовать следующие подходы:
1. Применение машинных методов
2. Раздельная минимизация и использование карт Карно.
3. Выделение подмножеств из функций системы для их совместной минимизации.
|
|
|
