 |
Переходные процессы в релейных САУ
|
|
|
|
Расчет переходного процесса в релейных системах осуществляют методом припасовывания. Метод припасовывания используют только для кусочно-линейных систем, смысл его состоит в разбиении нелинейности на ряд линейных участков. Дифференциальное уравнение разбивается на линейные дифференциальные уравнения для различных участков динамического процесса, которые решаются в общем виде для каждого линейного участка, затем находится решение в конце начального участка, которое принимается за начальное значение для следующего участка.
Представим, что F (х) принимает следующие значения:
Тогда дифференциальное уравнение системы при х ≤ - b примет вид:
(3.14.)
т.е. решением этого линейного дифференциального уравнения будет описан переходной процесс в системе, до тех пор, пока х < - b.
При значении b > х > - b уравнение примет следующий вид:
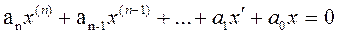(3.15.)
При этом начальными условиями для уравнения (3.15.) будут результаты решения уравнения (3.14.), т.е. значения х, х', х",..., хn, до тех пор, пока х ≤ - b.
Подобным образом при х ≥ + b от уравнения (3.15.) переходят к уравнению (3.16.), и получают следующее дифференциальное уравнение:
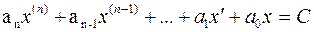(3.16.)
Основным недостатком метода припасовывания является сложность увязывания
переходов от одного линейного участка к другому, поэтому используют метод точечного преобразования – усовершенствованный метод припасовывания с использованием фазового пространства. С использованием метода точечного преобразования легче осуществляется переход от одного линейного участка к другому.
Контрольные тесты к разделу 3:
«НЕЛИНЕЙНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ»
|
|
|
Системы, не поддающиеся линеаризации с помощью метода малых отклонений, называются системами
а) с существенными статическими нелинейностями
б) с существенными динамическими нелинейностями
в) с статической ошибкой
г) с динамической ошибкой
Фазовым пространством называется
а) совокупность фазовых траекторий, полученных при различных начальных условиях
б) плоскость, в которой движется изображающая точка, при наличии в уравнении любого количества переменных
в) пространство, синфазное колебаниям изображающей точки
г) пространство, в котором движется изображающая точка
Фазовым портретом называется
а) совокупность фазовых траекторий, полученных при различных начальных условиях
б) совокупность фазовых траекторий, полученных при нулевых начальных условиях
в) плоскость, в которой движется изображающая точка, при наличии в уравнении любого количества переменных
г) пространство, в котором движется изображающая точка
Фазовой траекторией называется
а) плоскость, в которой движется изображающая точка, при наличии в уравнении любого количества переменных
б) пространство, в котором движется изображающая точка
в) траектория изображающей точки
г) траектория изображающей точки при начальных условиях
Фазовой плоскостью называется
а) плоскость, в которой движется изображающая точка, при наличии в уравнении всего двух переменных
б) совокупность фазовых траекторий, полученных при различных начальных условиях
в) плоскость, в которой движется изображающая точка, при наличии в уравнении любого количества переменных
г) пространство, в котором движется изображающая точка
При затухающем колебательном или апериодическом процессе направление фазовой траектории стремится к
а) - ∞
б) + ∞
в) различным значениям
г) нулю
|
|
|
|
|
|
