Потери напора при течении вязкой жидкости

Оглавление

Введение 3

Ключевые слова 4

1 Жидкость как жидкое тело 4

2 Потери напора при течении вязкой жидкости 4

2.1 Истечения через малые отверстия в тонкой стенке при постоянном напоре 9

3 Расход жидкости при истечении через отверстия 10

4 Гидравлический удар в трубопроводах 13

4.1 Причина гидроудара 13

4.2 Защита от гидроудара 14

Заключение 15

Список используемых источников 16

Приложение А 17

Приложение Б 22

 

 

 

Изм.

Лист

№ докум.

Подпись

Дата

Лист

РЕФЕРАТ ПО ВОДОСНАБЖЕНИЮ И ВОДООТВЕДЕНИЮ

Разраб.

Гриценко А.В.

Провер.

Нагрузова Л.П.

Т. Контр.

Ф.И.О.

Н. Контр.

Ф.И.О.

Утверд.

Ф.И.О.

Механика жидкости

Лит.

Листов

ХТИ филиал СФУ

Реценз.

Ф.И.О.

Масса

Масштаб

1: 1

ВВЕДЕНИЕ

В первую очередь стоит сказать что жидкости, это то с чем мы постоянно сталкиваемся в процессе нашей повседневной жизни (даже первое восприятие окружающего мира для детей сводится к тому, что все вокруг состоит из твердых тел и жидкостей). Мы встречаемся с одними видами жидкостей наблюдаем другие, но при этом каждого из нас иногда посещает мысль о том какими свойствами обладает та или иная жидкость, а зависит ли это от ее структуры или же происходит какое либо изменение в жидкостях под воздействием окружающей среды, а поменяется ли структура жидкости когда она будет находится под каким-то воздействием с которым она не встречалась при нормальных условиях. Да и вообще какие бывают разновидности жидкостей и какова их структура. На эти вопросы ищут ответы ученные в области физики при помощи изучения жидкостей разных видов путем проведения различных опытов, с целью выявления их физических и химических свойств

 

 

Ключевые слова

Жидкость, напор, сопротивление, истечение, расчет отверстие, расход жидкости, гидроудар, трубопровод.

 

1 Жидкость как жидкое тело

Когда мы говорим о жидкости как о сплошной среде, это вовсе не означает, что эта среда бесконечна и безгранична. Жидкое тело всегда имеет границы, это либо твёрдые стенки каналов, либо границы раздела с газообразной средой, либо это граница раздела между различными несмешивающимися жидкостями. Такие границы можно с полным правом называть естественными границами.
В некоторых случаях границы могут выделяться условно внутри самой движущейся жидкости. На естественных границах в пограничном слое жидкости между молекулами самой жидкости и молекулами окружающей жидкость среды существуют силы притяжения, которые, в общем случае, могут оказаться не равными. В то же время силы взаимодействия между остальными молекулами жидкости, находящимися внутри объёма, ограниченного пограничным слоем эти силы уравновешены.

Потери напора при течении вязкой жидкости

В протяженных трубопроводах становятся существенными поте­ри напора за счет трения жидкости о стенку трубы, приводящие к превращению части механической энергии в теплоту. Эта часть потерь напора называется потерями напора по длине трубы. К по­терям напора приводят также повороты, резкие сужения, расшире­ния и другие изменения геометрии трубы, способствующие вихре-образованию, приводящему тоже к превращению части механичес­кой энергии жидкости в теплоту. Эти препятствия потоку называ­ются местными сопротивлениями. Потери напора на местных сопротивлениях вычисляются по формуле Вейсбаха 1.5) где С — коэффициент местного сопротивления. Для плавного пово­рота трубы на 90°, например, f = 1,2-н 1,4. В некоторых случаях площадь поперечного сечения потока до и после местного сопротивления меняется, в результате чего сред­няя по сечению скорость течения будет тоже различной. Если нет специального замечания, то в формуле (1.5) в качестве v использу­ется скорость течения потока после прохождения им местного сопротивления.

Коэффициенты местного сопротивления получаются в большин­стве случаев экспериментальным путем и только для случая внезап­ного расширения — теоретически по формуле Борда

/(2g),

где — скорости жидкости до и после внезапного расширения сечения трубы.

Расчет поля скорости при ламинарном течении в трубе дал закон Пуазейля для потери напора на трение, распределенное по длине трубы

/(gd²) или

где L — длина трубы, d — диаметр, v — кинематический коэффи­циент вязкости, v— средняя по сечению скорость жидкости, Q — объемный расход.

Закон Пуазейля гласит: при ламинарном течении потери напора пропорциональны коэффициенту вязкости и объемному расходу в первой степени и обратно пропорциональны диаметру в четвертой степени.

Формулу закона Пуазейля можно привести к виду. Потери напора на трение по длине трубы тогда даются формулой Дарси Вейсбаха (ее иногда называют формулой Дарси)

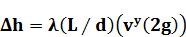(1.6)

где — коэффициент сопротивления, который характеризует влия­ние числа Рейнольдса на режим течения

. (1.7)

Отношение L/d представляет собой длину трубы, выраженную в калибрах диаметра. Таким образом комплексу (L/d) в формуле (1.6) соответствует коэффициент местного сопротивления £ в формуле (1.5).

При турбулентном режиме течения потери напора по длине определяют также по формуле Дарси Вейсбаха, но используют коэффициент сопротивления трения Я, полученный эксперименталь­но. Обширные и тщательные измерения коэффициента сопротивле­ния трения провел И. И. Никурадзе. Среди большого числа имеющихся формул следует выделить формулу Блазиуса для гидрав­лически гладких труб

=0,3164/Re°’²⁵ (Re>2300). (1.8)

Так как коэффициент сопротивления незначительно меняется с из­менением величины скорости v: обратно пропорционально v в степе­ни 0,25, при турбулентном течении потери напора на трение соглас­но формуле (1.6) приблизительно пропорциональны квадрату ско­рости или квадрату объемного расхода.

Для гидравлически шероховатых труб при турбулентном режи­ме течения

где -эквивалентная абсолютная шероховатость, измеряемая в тех же единицах, как и диаметр d, чтобы отношение Δ/d было безразмерным. Это формула А. Д. Альтшуля. При больших значе­ниях числа Рейнольдса Re член 68/Re выпадает и величина Я пере­стает зависеть от числа Re. Тогда закон зависимости потерь напора Ah от скорости v становится квадратичным.

Три приведенные выше формулы (1.7), (1.8), (1.9) дают зави­симость коэффициента сопротивления я от числа Рейнольдса Re, представленную на рис. 1.8 в области 1—для ламинарного течения, в области 2 — для турбулентного течения в гладких тру­бах, в области 3 — для квадратичного режима течения в шерохова­тых трубах с различной эквивалентной абсолютной шероховато­стью А.

В водопроводе коэффициент сопротивления Λ принято рассчиты­вать по формулам Ф. А. Шевелева для стальных и чугунных труб.

При скорости v˂1,2 м/с Λ=(1,5• 10~⁴/d+l/Re)^0,3; при скорости v > 1,2 м/с Λ=0,21d°’³, где d — диаметр, м.

Формулы получены на основании обобщения большого количе­ства опытных данных, на водопроводных магистралях больших диаметров.

При расчете потерь напора h по длине трубопровода используют также понятие гидравлического уклона 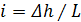представляющего собой величину потерь напора на единице длины трубы

Рис. 1.8. Характер зависимости коэффициента сопротивления от числа Рейнольдса при ламинар­ном течении 1 и турбулентном течении я гладких 2 и в шерохо­ватых трубах с различной экви­валентной абсолютной шерохо­ватостью 3

, где L — длина трубы, на которой происходит потеря напора Δh.

Движение жидкости в каналах с открытой свободной поверхно­стью, имеющих геометрический ук­лон дна /д, происходит в безнапор­ном режиме, так как поверхность потока непрерывно соприкасается с атмосферой. В конце XVIII в. фра­нцузским гидравликом Шези (Chezy) была установлена формула для рас­чета скорости течения в реках и ка­налах

и

объемного расхода воды 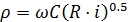⁵, где w — площадь живого сечения потока, R — гидравлический ра­диус, R=ω/x, X — смоченный периметр живого сечения потока, С — коэффициент Шези. Эти формулы были установлены первоначально для течений с открытой поверхностью воды для так называемых безнапорных течений, а затем были распространены на течения в трубах и кана­лах с полным заполнением их поперечного сечения без открытой поверхности (напорные течения). В конце XVIII в. полагали, что С является постоянной величиной, равной 50 м^0,5/с при измерении линейного размера (в м), а времени (в с) во всех остальных вели­чинах. Дальнейшие обширные экспериментальные исследования, обобщенные Н. Н. Павловским, дали для коэффициента Шези формулу

C=n-¹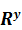

где у =1/6, п — коэффициент шероховатости берется по данным Гаити лье Куттера и составляет 0,011 для чугунных и железных труб; 0,015 для кирпичной кладки; 0,035 для дна и берегов реки. Анализ формул дал связь коэффициента Шези С с коэффициентом сопротивления Я для течения в трубе

С=(8g/Λ)°-³, где g=9,81 м/с².

Подставив в эту формулу значение С=50 м^0,3/с и разрешив ее относительно X, получим, что Λ=0,0332. В действительности во многих практически важных случаях коэффициент сопротивления Λ, вычисленный по формулам (1.7), (1.8), оказывается находящимся в пределах 0,01 — 0,03.

Поток жидкости или газа, движущийся с большой скоростью, может поднимать и переносить на большое расстояние твердые частицы, обладающие значительно большей плотностью р„, чем жидкость или газ. Проявление этого мы видим в реке, несущей песок в придонных областях течения, в атмосфере при пылевой или снежной буре. Подъем и взвешивание в потоке тяжелых твердых частиц происходит за счет возникновения вихрей и турбулентных пульсаций скорости и давления, имеющих вертикальную состав­ляющую, а также за счет действия подъемной силы на частицы несимметричной формы.

Считается, что твердые частицы могут оказаться во взвешенном состоянии, если скорость вертикальных пульсаций сравнима по величине со скоростью осаждения частиц в спокойной неподвижной среде, вычисляемой по формуле

v=gd²(p_n-p)/(l8u),

где p — плотность жидкости или газа, р — коэффициент вязкости.

Было введено понятие критической скорости v^,, при которой твердые частицы диаметра d и плотности р_п будут взвешиваться потоком и транспортироваться на большие расстояния. Согласно формуле Смолдырева в потоке воды критическая скорость со­ставляет

v_wp=(0,7/1)((p_n-p)gdl/p)°-⁵,

где d — диаметр трубопровода, р — плотность воды, g=9,8 м/с².

По этому принципу работают земснаряды и установки для гидр о- и пневмотранспорта сыпучих грузов на большие расстояния, канализационные системы.

Важной характеристикой взвесенесущего потока является массовая концентрация в нем твердого вещества с, являющаяся от­ношением массы твердого вещества, содержащегося в единице объема т„, к массе т всего вещества в этом объеме (включая жидкую фазу и газообразную)

c—mtBm. Земснаряды и гидротранспортные установки работают обычно с концентрацией твердого с от 0,05 до 0,50. В канализационной системе концентрация твердых включений составляет около с=0,01.

2.1 Истечение через малые отверстия в тонкой стенке при постоянном напоре

 

Рассмотрим большой резервуар с жидкостью под давлением Р₀, имеющий малое круглое отверстие в стенке на достаточно большой глубине Н₀ от свободной поверхности (рис.5.1). Жидкость вытекает в воздушное пространство с давлением Pi. Пусть отверстие имеет форму,

Рис. 5.1. Истечение из резервуара через малое отверстие

показанную на рис.5.2, а, т.е. выполнено в виде сверления в тонкой стенке без обработки входной кромки или имеет форму, показанную на рис.5.2, б, т.е. выполнено в толстой стенке, но с заострением входной кромки с внешней стороны. Струя, отрываясь от кромки отверстия, несколько сжимается (рис.5.2, а). Такое сжатие обусловлено движением жидкости от различных направлений, в том числе и от радиального движения по стенке, к осевому движению в струе.

В данном случае, когда боковые стенки и свободная поверхность не влияют на приток жидкости к отверстию, наблюдается совершенное сжатие струи, т.е. наибольшее сжатие в отличие от несовершенного.

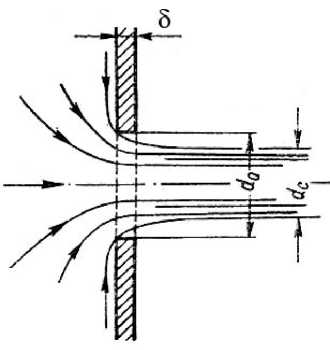
Рис (5.2) (а) (б)

12Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: