Действия над обобщенными функциями

Анализ обобщенных функций

Введение

Существуют многие физические модели, которые в терминах обычных функций не могут быть описаны. Например, распределение зарядов вдоль прямой удобно задать плотностью этого распределения. Однако, если на прямой существуют точки, несущие заряды, то плотность такого распределения не может быть описана "обычной" функцией. Другой пример связан с определением производной в точках разрыва функции, когда эта операция носит в выкладках промежуточный характер.

Определение. Основное пространство K^m состоит из действительных функций j (t), называемыми основными функциями, имеющими непрерывные производные до порядка m включительно, равными нулю вместе со всеми производными вне конечного интервала. Пространство K^m является линейным.

Пример. Рассмотрим функцию

 

 

график которой приведен ниже

 

j

1

 

a (a+b)/2 b t

 

Эта функция принадлежит основному пространству K^o, так как не существуют производные в точках t = a и t = b. Функция (график смотри ниже)

 

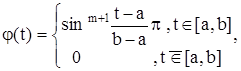
принадлежит пространству K^m.

 

j

1

a (a+b)/2 b t

 

Если положить m = ¥ для основного пространства K^m, то полученное основное пространство обозначается К. Пусть

 

 

тогда, как легко проверить, j(t) Î K.

 

 

Обобщенные функции

Определение. Обобщенной функцией f (t) (заданной на прямой (-¥ < t <¥)) называется всякий непрерывный линейный функционал на пространстве основных функций. Он может быть представлен в виде скалярного произведения

 

(f (t), j (t)), j (t) Î K (K^m).

 

Всякая интегрируемая функция f (t) порождает обобщенную функцию, так как скалярное произведение

 

 

есть непрерывный линейный функционал на K. Такие обобщенные функции называются регулярными, остальные (которые не допускают такого представления) – сингулярными. Приведем пример сингулярной обобщенной функции. С этой целью рассмотрим последовательность функций

 

 

Так как интеграл Пуассона

 

 то  (1)

При n®¥ функция d_n(t) вытягивается до бесконечной высоты в точке t = 0, а вне ее становится равной нулю, сохраняя свойство (1). В обычном понимании предел d_n(t) при n®¥ не существует. Предел

 

lim d_n(t) = d(t)

n®¥

 

можно рассматривать как обобщенную функцию, то есть функцию, которая порождается скалярным произведением

 

 (2)

 

где j (t) – основная функция. Скалярное произведение (2.) есть линейный непрерывный функционал на пространстве основных функций (j Î K). Функция d(t) называется дельта – функцией (обобщенная функция Дирака).

Определим произведение обобщенной функции f на число l соотношением

 

(l f, j) = l (f, j) (j Î K).

 

Сумма двух обобщенных функций f₁, f₂ определим следующим образом

 

(f₁ + f₂, j) = (f₁, j) + (f₂, j) (j Î K).

 

После этого множество обобщенных функций K' становится линейным пространством.

Определение. Две обобщенные функции f (t), g (t) Î K' равны: f (t) = g (t), если для любой основной функции j (t)

 

(f, j) = (g, j) или (f – g, j) = 0.

 

Обобщенная функция f (t) равна нулю: f = 0, если для любой основной функции j (t)

 

(f, j) = 0.

 

Примеры обобщенных функций.

1. Пусть j Î K. Определим обобщенную функцию f с помощью функционала

 

 

Приведенная сумма конечна, так как основная функция j(t) равна нулю вне некоторого конечного интервала.

2. Введенную ранее дельта-функцию d (t) определим следующим образом

 

(d (t), j(t)) = j(0).

Исходя из интегрального представления (2), имеем

 

Если а(t) – непрерывная функция, то

(а(t) d(t), j(t)) = (d(t), а(t) j(t)) = a(o) j(o) (j Î K^o).

Отметим, что функционал f, определенный на K соотношением

не является обобщенной функцией, так как, являясь непрерывным функционалом, он не линеен.

3. Обобщенная функция Хевисайда

 

для которой можно записать

 

 

является регулярной обобщенной функцией.

 

Действия над обобщенными функциями

 

Введем в пространстве обобщенных функций K' операцию предельного перехода. Последовательность  сходится к f, если для любого j Î K выполнено следующее соотношение

 

(f_n, j) ® (f, j)

n ®¥

 

Определим теперь для обобщенных функций операцию дифференцирования и рассмотрим ее свойства. Производная f '(t) регулярной обобщенной функции f (t) равна

 

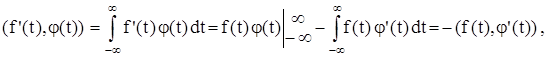
так как основная функция обращается в нуль вне некоторого конечного интервала. Производная n – го порядка будет тогда определяться равенством

 

(f⁽ⁿ⁾ (t), j(t) = (-1)ⁿ (f (t), j⁽ⁿ⁾ (t)) (" n Î N, j Î K).

 

Это соотношение определяет производную n – го порядка обобщенных функций, включая и сингулярные функции.

Примеры:

1. Производная функции Хевисайда равна

2. Так как

то

 

Из определения дельта – функции следует

t d(t) = 0,

а значит

 

d(t) + t d'(t) = 0,

2d'(t) + t d''(t) = 0,

---------------------

nd^(n-1)(t) + t d⁽ⁿ⁾(t) = 0.

12	Поделиться:

Воспользуйтесь поиском по сайту: