Дифференциальные уравнения в обобщенных функциях

 

Рассмотрим уравнение

 

 

Если f(t) – обычная функция, то его решением является первообразная, то есть

 

 

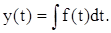
Пусть теперь f(t) – обобщенная функция.

Определение. Обобщенная функция g(t) называется первообразной обобщенной функцией f(t), если

 

(g'(t), j(t)) = (f (t), j(t)).

 

Если f(t) – сингулярная обобщенная функция, то возможны случаи, когда ее первообразная – регулярная обобщенная функция. Например, первообразная d(t) является y(t) = q(t); первообразная q(t) является функция y(t) = t₊, а решение уравнения

 

y''(t) = d(t)

 

можно записать в виде

 

t(t) = t₊ + C₁t + C₂ (C₁, C₂ = const).

Рассмотрим линейное уравнение n-го порядка с постоянными коэффициентами

 

 (4)

где f(t) – обобщенная функция. Обозначим

 

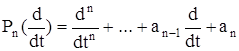
дифференциальный полином n-го порядка.

Определение. Обобщенным решением дифференциального уравнения (4) называется обобщенная функция y(t), для которой выполняется соотношение

 

 

Если f(t) – непрерывная функция, тогда единственным решением уравнения (4.) является классическое решение.

Определение. Фундаментальным решением уравнения (4) называется любая обобщенная функция e(t) такая, что

 

 

Функция Грина – фундаментальное решение, удовлетворяющее данному граничному, начальному или асимптотическому условию.

Теорема. Решение уравнения (4) существует и имеет вид

 

 (5)

если только свертка определена.

Доказательство. Действительно,

 

 

По свойству свертки имеем

 

 

В качестве примера рассмотрим уравнение

 

 (6)

 

Нетрудно видеть, что фундаментальным решением этого уравнения является

 

так как

и

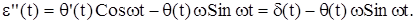
Поэтому

 

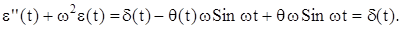
6. Пространство обобщенных функций

 

Совокупность обобщенных функций, порождаемых основным пространством K, образует пространство K'. Рассмотрим подпространство обобщенных функций  пространства K, состоящее их обобщенных функций, равных нулю вне некоторого конечного интервала принадлежащего [0, ¥]. Введем в этом пространстве операцию умножения двух функций в виде свертки этих функций. Если f(t), g(t) Î  то и  Кроме того свертка обладает всеми свойствами обычной операции умножения. Роль единицы в  играет функция d(t), так как для

 

Пусть существует  такая что

 

 

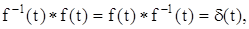
тогда f^-1(t) называется обратной обобщенной функцией f(t).

Пространство 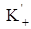 с введенной операцией умножения образует алгебру (коммутативную) со сверткой.

Рассмотрим алгебру со сверткой 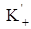 . Обобщенная функция  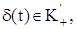так как она равна нулю всюду, кроме точки ноль. Обобщенная функция сосредоточена вначале координат, поэтому  Далее,

 

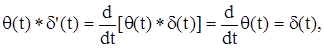
поэтому

 

Теорема. Пусть для  существуют обратные функции f ^{- 1}(t) и g^-1(t). Тогда свертка  имеет обратную функцию вида

 

 

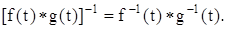
Действительно,

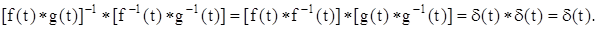
Рассмотрим следующее определенное в  уравнение в свертках

 

 

Свертка существует для любой обобщенной функции  так как

 

 

Следовательно, y(t) является фундаментальным решением уравнения (4). В частности, фундаментальное решение уравнения (6) с оператором 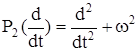 принадлежит алгебре со сверткой  Следовательно,

 

Рассмотрим операционный метод решения уравнения в свертках. Пусть имеется уравнение

 

 

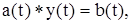
где a(t) и b(t) Î  Среди эффективных методов решения этого уравнения приведем метод преобразования Лапласа. Применив преобразование Лапласа к левой и правой части этого уравнения, имеем

Отсюда следует

 

 

Если для функции L(p) существует оригинал, принадлежащий 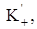 то он и является искомым решением.

В качестве примера рассмотрим уравнение

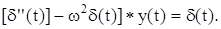
Применив к нему преобразование Лапласа, получим (р²-w²) L[y(t)] = 1.

Следовательно,

 

 

Откуда находим решение

 

Задача Коши

 

12	Поделиться:

Воспользуйтесь поиском по сайту: