 |
Алгоритмический анализ задачи
|
|
|
|
Постановка задачи
В курсовой работе необходимо:
С использованием системы MathCAD исследовать зависимость диаметра балки от Q1, максимального прогиба балки от P4. Построить графики этих зависимостей, изменяя последовательно Q1 и P4.
Определить численно опорную реакцию, используя функции MathCAD.
Построить эпюру поперечных сил и изгибающего момента.
Произвести расчет на прочность. Определить минимальный диаметр балки, используя характеристики материала;
Сделать выводы по полученным результатам.
Описание математической модели
Под действием внешних сил в сечении балки возникает осевой момент сопротивления, момент инерции, при этом точки оси перемещаются. Изогнутая ось балки называется упругой линией, а перемещение точек оси по нормали к ее недеформируемой оси есть прогиб балки. При этом длина оси остается неизменной.
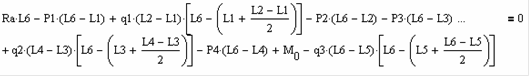


Исходными данными для работы являются:


Рис. 1
Описание документа MathCAD
Пакет MathCAD создан разработчиками для облегчения работы инженеров расчётчиков. Математические пакеты, в особенности MathCAD, позволяют специалистам в конкретной научно-технической области очень быстро освоить работу на компьютере и реализовать на них математические модели, не вдаваясь в тонкости программирования на традиционных языках.
Интегрированная система MathCAD предназначена для решения различного рода вычислительных задач, алгоритмы которых записываются в общепринятых математических терминах и обозначениях и позволяет:
выполнять вычисления арифметических выражения, которые могут содержать встроенные математические функции и функции пользователя;
решать нелинейные алгебраические и трансцендентные уравнения, а также систему уравнений и неравенств;
|
|
|
выполнять вычисление сумм, произведений определённых интегралов и производных в заданных точках;
осуществлять многочисленные операции с векторами включая линейную, кубическую и сплайн интерполяцию, а также расчёт статических оценок регрессионного анализа;
выполнять построение графиков различных форматов включая поддержку линии сетки, выделение расчётных кочек различными символами, а также размещение в одной графической области нескольких графиков;
оформлять вычисления с единицами измерений;
осуществлять чтение и запись данных файлов и т.д.
Описание исследований по модели
Составили уравнение равновесия опоры для определения реакции опоры:

Определяем поперечную силу Q в зависимости координаты x:
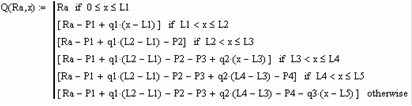
Определяем величину момента M в зависимости координаты x:

Строим эпюру поперечной нагрузки:

Рис. 2
Изменение величины момента в зависимости координаты x:

Рис. 3
При положительном изгибающем моменте верхние продольные слои материала испытывают сжатие, а нижние - растяжение.
Расчет на прочность.
Находим экстремальные значения изгибающего момента:

Минимальный осевой момент сопротивления сечения вычисляется по формуле:

Минимальный диаметр балки вычисляется по формуле:

Момент инерции вычисляется по формуле:

Реакция единичной нагрузки:

Реакция единичного момента:

Прогиб балки:

Угол поворота:

Максимальный прогиб и угол поворота балки:

Рис. 4
Для исследования зависимости диаметра балки от силы Q1, постепенно увеличиваем нагрузку:

Рис. 5
Изменяя силу P4, исследуем зависимость максимального прогиба балки от этой силы:

Рис. 6
|
|
|


