Нефтегазовое дело» Группа 1 Подгруппа 1

Номер студента в журнале

ЗАДАЧИ

Нефтегазовое дело» Группа 1 подгруппа 2

Номер студента в журнале

ЗАДАЧИ

Нефтегазовое дело» Группа 2 подгруппа 1

Номер студента в журнале

ЗАДАЧИ

Нефтегазовое дело» Группа 2 подгруппа 2

Номер студента в журнале

ЗАДАЧИ

Нефтегазовое дело» Группа 3 подгруппа 1

Номер студента в журнале

ЗАДАЧИ

Нефтегазовое дело» Группа 3 подгруппа 2

Номер студента в журнале

ЗАДАЧИ

Нефтегазовое дело» Группа 4 подгруппа 1

Номер студента в журнале

ЗАДАЧИ

Нефтегазовое дело» Группа 4 подгруппа 2

Номер студента в журнале

ЗАДАЧИ

Электромагнетизм

Глава 1. Электростатика

Контрольные вопросы

1. Что такое электризация? Какие тела называются наэлектризованными?

2. Что такое элементарный заряд? Чему он равен?

3. Сформулируйте закон сохранения электрического заряда.

4. Запишите в СИ закон Кулона.

5. В чем состоит принцип независимого взаимодействия зарядов?

6. Что такое напряженность электростатического поля? Как направлен вектор напряженности?

7. В чем состоит принцип суперпозиции полей?

8. Какая линия называется силовой или линией напряженности?

9. Как связаны между собой индукция и напряженность электростатического поля?

10. Дайте понятие потока индукции (напряженности) электростатического поля. Запишите общую формулу для нахождения потока индукции (напряженности) через площадку S.

11. Сформулируйте теорему Остроградского – Гаусса. Приведите примеры ее использования для расчета полей.

12. Чему равна работа перемещения заряда в электростатическом поле?

13. В чем состоит потенциальность электростатического поля?

14. Что такое потенциал? Как вычислить потенциал поля точечного заряда?

15. Как связаны между собой напряженность и потенциал электростатического поля? (Покажите на примерах).

Основные формулы

Закон Кулона

,

где F - сила взаимодействия двух точечных зарядов q ₁ и q ₂, находящихся на расстоянии r, e - относительная диэлектрическая проницаемость среды, e₀ - электрическая постоянная, равная 8,85× 10^-12 Ф/м.

Напряженность и потенциал электростатического поля

,

где F - сила, действующая на положительный точечный заряд q ₀, помещенный в данную точку поля;

,

где W _п - потенциальная энергия заряда q ₀ в данной точке поля, 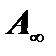- работа по перемещению заряда q ₀ из данной точки поля за его пределы.

Напряженность и потенциал электростатического поля точечного заряда q на расстоянии r от заряда

; .

Принцип суперпозиции (наложения) электростатических полей

; , где и - напряженность и потенциал поля, созданного зарядом q _i.

 

Электрическое смещение

.

Поток вектора напряженности (индукции) через произвольную поверхность S

;

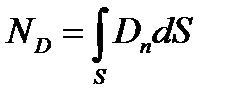
Теорема Гаусса - поток вектора напряженности (индукции) через замкнутую поверхность S

;

Линейная, поверхностная и объемная плотности заряда

; ; .

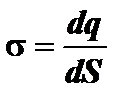Напряженность полей:

 

а) равномерно заряженной бесконечной плоскости

;

б) двух параллельных бесконечных равномерно заряженных плоскостей

;

в) равномерно заряженной сферы радиуса R на расстоянии r от ее центра

E = 0, при r < R (внутри сферы),

при r ³ R;

г) объемно заряженного шара радиусом R на расстоянии r от его центра

, при r < R (внутри шара),

, при r ³ R (вне шара);

д) равномерно заряженного бесконечного цилиндра радиуса R на расстоянии r от него

E = 0, при r < R (внутри цилиндра),

, при r ³ R (вне цилиндра).

Работа, совершаемая силами поля, при перемещении заряда q ₀ из т.1 в т.2

,

где E_l - проекция вектора 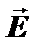на направление элементарного перемещения .

Связь между напряженностью и потенциалом .

В случае плоского конденсатора

,

где U - разность потенциалов между пластинами, d - расстояние между ними.

Методические указания

 

1. Одна из главных задач электростатики - нахождение напряженности электростатического поля по известному распределению зарядов. При решении этой задачи могут встретиться три случая.

 

а. Поле создано точечными зарядами. Для ее решения используют формулу напряженности поля точечного заряда и принцип суперпозиции.

б. Поле создано зарядами, которые не являются точечными, но равномерно распределены по сферическим, цилиндрическим или плоским поверхностям. В этом случае применяют формулы, полученные с помощью теоремы Остроградского - Гаусса.

в. Если заряженное тело не является ни сферой, ни цилиндром, ни плоскостью, то для расчета поля необходимо разбить его на бесконечно малые элементы и записать от каждого из них, как от точечного заряда, элементарную напряженность 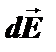поля в данной точке, а затем просуммировать все элементарные напряженности, т.е. взять интеграл. Это наиболее общий метод ДИ - метод дифференцирования - интегрирования.

 

2. Если в задачах не указана среда, в которой рассчитывается поле, то подразумевается вакуум (или воздух), т.е. e = 1.

3. Полезно помнить, что k = 1/4pe₀ = 9,00×10⁹ м/Ф.

4. Для нахождения потенциала поля, созданного системой точечных зарядов, применяются формулы для потенциала поля точечного заряда и принцип суперпозиции.

5. Следует иметь ввиду, что главный физический смысл имеет не сам потенциал, а разность потенциалов. В основе общего метода нахождения разности потенциалов лежит формула 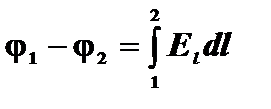. Она следует из связи напряженности и потенциала , где производная берется в направлении быстрейшего изменения потенциала, т.е. вдоль силовой линии.

ЗАДАЧИ

1. Два точечных заряда, находясь в воздухе на расстоянии 20 см друг от друга, взаимодействуют с некоторой силой. На каком расстоянии необходимо поместить эти заряды в масле, чтобы получить ту же силу взаимодействия?

[8,94 см]

2. Во сколько раз энергия электростатического взаимодействия двух частиц с зарядом q и массой m каждая больше энергии их гравитационного взаимодействия? Задачу решить для: а) электронов; б) протонов.

[4,17×10⁴²; 1,24×10³⁶ ]

3. Найти напряженность электрического поля в точке, лежащей посередине между двумя точечными зарядами 8 нКл и -6 нКл. Расстояние между зарядами 10 см; заряды находятся в вакууме.

[50,4 кВ/м]

4. В центр квадрата, в каждой вершине которого находится заряд 2,33 нКл, помещен отрицательный заряд. Найти этот заряд, если на каждый заряд действует результирующая сила F = 0.

[-2,23 нКл]

5. Два точечных заряда 7,5 нКл и -14,7 нКл расположены на расстоянии 5 см. Найти напряженность Е электрического поля в точке, находящейся на расстояниях 3 см от положительного заряда и 4 см от отрицательного заряда.

[112 кВ/м]

 

6. Составить задачу на произвольный треугольник.

7. Два шарика одинаковых радиуса и массы подвешены на нитях одинаковой длины так, что их поверхности соприкасаются. После сообщения шарикам заряда 0,4 мкКл они оттолкнулись друг от друга и разошлись на угол 60⁰. Найти массу каждого шарика, если расстояние от центра шарика до точки подвеса 20 см.

[1,56 г]

8. Два шарика одинаковых радиуса и массы подвешены на нитях одинаковой длины так, что их поверхности соприкасаются. Какой заряд нужно сообщить шарикам, чтобы сила натяжения нитей стала равной 98 мН? Расстояние от центра шарика до точки подвеса 10 см; масса каждого шарика 5 г.

[1,1 мкКл]

9. На рисунке АА – заряженная бесконечная плоскость с поверхностной плотностью заряда 40 мкКл/м² и В – одноименно заряженный шарик с массой 1 г и зарядом 1 нКл. Какой угол с плоскостью АА образует нить, на которой висит шарик?

[13⁰]

10. На рисунке к задаче 9, АА – заряженная бесконечная плоскость и В – одноименно заряженный шарик с массой 0,4 мг и зарядом 667 пКл. Сила натяжения нити, на которой висит шарик, 0,49 мН. Найти поверхностную плотность заряда на плоскости АА.

[7,8 мкКл/м²]

11. Медный шар с радиусом 0,5 см помещен в масло. Плотность масла 0,8×10³ кг/м³. Найти заряд шара, если в однородном электрическом поле шар оказался взвешенным в масле. Электрическое поле направлено вертикально вверх и его напряженность 3,6 МВ/м.

[11 нКл]

12. В плоском горизонтально расположенном конденсаторе заряженная капелька ртути находится в равновесии при напряженности электрического поля 60 кВ/м. Заряд капли 0,8×10^-18 Кл. Найти радиус капли.

[0,44 мкм]

13. Шарик массой 40 мг, имеющий положительный заряд 1 нКл движется со скоростью 10 см/с. На какое расстояние может приблизиться шарик к положительному точечному заряду 1.33 нКл?

[6 см]

14. Два шарика с зарядами 6,66 нКл и 13,33 нКл находятся на расстоянии 40 см. Какую работу надо совершить, чтобы сблизить их до расстояния 25 см?

[1,2 мкДж]

15. Найти потенциал точки поля, находящейся на расстоянии 10 см от центра заряженного шара радиусом 1 см. Задачу решить, если: а) задана поверхностная плотность заряда на шаре, равная 0,1 мкКл/м²; б) задан потенциал шара, равный 300 В.

[а) 11,3 В; б) 30 В]

16. Какая работа совершается при перенесении точечного заряда 20 нКл из бесконечности в точку, находящуюся на расстоянии 1 см от поверхности шара радиусом 1 см с поверхностной плотностью заряда 10мкКл/м²?

[113 мкДж]

17. Шарик с массой 1 г и зарядом 10 нКл перемещается из точки 1, потенциал которой 600 В, в точку 2, потенциал которой 0 В. Найти его скорость в точке 1, если в точке 2 она стала равной 20 см/с.

[16,7 см/с]

⇐ Предыдущая12345678Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: