 |
Законы распределения случайной величины. Нормальный закон
|
|
|
|
Случайные величины имеют разные законы распределения.
В некоторых задачах практики встречаются непрерывные случайные величины, о которых заранее известно, что их возможные значения лежат в пределах некоторого определенного интервала; кроме того, известно, что в пределах этого интервала все значения случайной величины одинаково вероятны (точнее, обладают одной и той же плотностью вероятности). О таких случайных величинах говорят, что они распределяются по закону равномерной плотности.
Непрерывная случайная величина Х, принимающая только положительные значения имеет показательное (или экспоненциальное) распределение, если
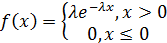
где 
- параметр показательного распределения, полностью определяющий его.
Интервал времени между двумя соседними событиями в простейшем потоке имеет показательное распределение с параметром, равным интенсивности потока. Например, наработка объекта на отказ (время до очередного выхода объекта из работоспособного состояния) распределяется по экспоненциальному закону с интенсивностью равной
где 
– среднее время между отказами.
Наибольший интерес при выполнении измерений представляет нормальный закон распределения (распределение Гаусса).
Нормальный закон распределения играет исключительно важную роль в теории вероятностей и занимает среди других законов распределения особое положение. Это - наиболее часто встречающийся на практике закон распределения. Главная особенность, выделяющая нормальный закон среди других законов, состоит в том, что он является предельным законом, к которому приближаются другие законы распределения при весьма часто встречающихся типичных условиях.
|
|
|
Можно доказать, что сумма достаточно большого числа независимых (или слабо зависимых) случайных величин, подчиненных каким угодно законам распределения, приближенно подчиняется нормальному закону, и это выполняется тем точнее, чем большее количество случайных величин суммируется. Большинство встречающихся на практике случайных величин, таких, например, как ошибки измерений, ошибки стрельбы и т. д., могут быть представлены как суммы весьма большого числа сравнительно малых слагаемых - элементарных ошибок, каждая из которых вызвана действием отдельной причины, не зависящей от остальных. Каким бы законам распределения ни были подчинены отдельные элементарные ошибки, особенности этих распределений в сумме большого числа слагаемых нивелируются, и сумма оказывается подчиненной закону, близкому к нормальному.
Основное ограничение, налагаемое на суммируемые ошибки, состоит в том, чтобы они все равномерно играли в общей сумме относительно малую роль.
Нормальный закон распределения характеризуется плотностью вероятности вида:
.
Вероятность попадания случайной величины в интервал от a до b определяется зависимостью
(8)
или, используя т.н. функцию Лапласа (
), значения которой табулированы (Прил. 1),
Для нормально распределенной случайной величины все рассеяние с точностью до 1% (99% реализаций величины) укладывается в интервале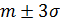 
.
Нормальный закон описывает распределение случайной величины на интервале от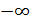 
до 
. Однако, как правило, интервал распределения случайной величины ограничен конкретными значениями величины a и b. В таком случае используется усеченный нормальный закон распределения 
, отличающийся множителем – нормирующим коэффициентом, который определяется по зависимости
. (9)
Ошибки измерений
Численное значение физической величины получается в результате ее измерения, т. е. сравнения ее с другой величиной того же рода, принятой за единицу. При проведении измерений получение точного значения измеряемой величины физически невозможно. Исследователь получает значение величины с некоторым отклонением, называемым ошибкой измерения. Ошибкой измерения называется разность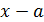 
между результатом измерения 
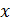и истинным значением 
измеряемой величины. Ошибка измерения обычно неизвестна, как и истинное значение величины. Ошибки измерения имеют разные величины, вызываются разными причинами и классифицируются следующим образом.
|
|
|
Грубые ошибки возникают вследствие нарушения основных условий измерения или в результате недосмотра экспериментатора. При обнаружении грубой ошибки результат измерения следует сразу отбросить, а само измерение повторить (если это возможно). Внешним признаком результата, содержащего грубую ошибку, является его резкое отличие по величине от результатов остальных измерений.
Ошибки измерения вызываются большим количеством разнообразных причин (факторов). Иногда в проведенной серии измерений один из факторов оказывается превалирующим. Например, если после измерений обнаружена неправильная регулировка прибора, которая привела к смещению начала отсчета, то все снятые показания будут смещены либо на постоянную величину, если шкала прибора равномерна, либо на величину, изменяющуюся по определенному закону, если шкала прибора неравномерна. Другим примером может служить изменение внешних условий, например, температуры, если известно влияние этих изменений на результаты измерений.
Принято говорить, что каждая из таких причин вызывает систематическую ошибку. Обнаружение таких ошибок довольно трудозатратно, но результаты измерений легко исправимы.
Ошибки измерения, остающиеся после устранения всех выявленных систематических ошибок, т. е. ошибки результатов измерений, исправленных путем введения соответствующих поправок, называются случайными. Случайные ошибка вызываются большим количеством таких факторов, эффекты действия которых столь незначительны, что их нельзя выделить и учесть в отдельности. Случайную ошибку можно рассматривать как суммарный эффект действия таких факторов.
Случайные ошибки являются неустранимыми, их нельзя исключить в каждом из результатов измерений. Но с помощью методов теории вероятностей можно учесть их влияние на оценку истинного значения измеряемой величины, что позволяет определить значение измеряемой величины со значительно меньшей ошибкой, чем ошибки отдельных измерений.
|
|
|
Для оценки достоверности результатов измерений вводятся в рассмотрение понятия доверительного интервала и доверительной вероятности.
Доверительным называется интервал значений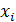 
, в который попадает истинное значение 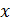измеряемой величины с заданной вероятностью.
Доверительной вероятностью (достоверностью) измерения называется вероятность того, что истинное значение измеряемой величины попадает в данный доверительный интервал, т.е. в зону 
. Эта величина определяется в долях единицы или в процентах
,
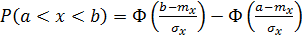где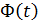 
- интегральная функция Лапласа (Прил. 1).
Интегральная функция Лапласа определяется следующим выражением:
.
Аргументом этой функции является гарантийный коэффициент:
, (10)
где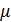 
– половина доверительного интервала, 
.
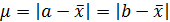Если же на основе определенных данных установлена доверительная вероятность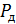 
(часто ее принимают равной 0.95, 0.99 или 0.999 в зависимости от степени ответственности расчета), то устанавливается точность измерений (доверительный интервал 
) на основе соотношения
.
Половина доверительного интервала равна
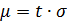, (11)
где 
- аргумент функции Лапласа, если 
(Прил. 1);
- аргумент функции Стьюдента, если 
(Прил. 2). В последнем случае, зависит не только от доверительной вероятности, но и от степени свободы 
.
Таким образом, доверительный интервал характеризует точность измерения данной выборки, а доверительная вероятность (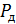) - достоверность измерения.
Значение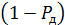 
называют уровнем значимости. Из него следует, что при нормальном законе распределения ошибок погрешность, превышающая доверительный интервал, будет встречаться один раз из 
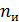измерений, где
.
Это означает, что приходится браковать одно из 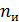измерений.
|
|
|
