 |
Интегральная функция распределения.
|
|
|
|
Теория вероятностей.
Лекция №1. Понятие вероятности. Элементы комбинаторики.
Предмет теории вероятностей. Понятие события. Несовместные, достоверные, невозможные, противоположные события. Полная группа событий. Относительная частота и вероятность события. Элементы комбинаторики.
Предмет теории вероятностей. Понятие события.
События, которые происходят в окружающем нас мире можно разделить на две группы:
- Детерминированные события (не случайные, предопределенные) – к которым относятся достоверные и невозможные события.
- Стохастические (случайные).
Оп. Испытание – создание совокупности начальных условий, при которых может произойти (или не произойти) интересующее нас событие.
Оп. Достоверным (невозможным) называется событие, которое обязательно произойдет (не произойдет) в результате испытания. Случайное событие ( СС ) – это событие, которое может произойти или не произойти в результате испытания.
СС будем обозначать заглавными буквами латинского алфавита  .
.
Оп. Теория вероятностей (ТВ) – раздел высшей математики, в котором изучаются закономерности проявления СС массового характера.
Действия над событиями. Виды событий.
Оп. Суммой СС  и
и  будем называть СС
будем называть СС  , которое состоит в проявлении хотя бы одного из событий слагаемых. Произведением СС
, которое состоит в проявлении хотя бы одного из событий слагаемых. Произведением СС  и
и  будем называть СС
будем называть СС  , которое состоит в совместном наступлении событий сомножителей.
, которое состоит в совместном наступлении событий сомножителей.
Пример. Выпадение четного числа очков на грани игрального кубика при однократном подбрасывании  , где
, где  .
.
Выпадение на двух игральных кубиках суммы очков равной двум – СС  , где СС
, где СС  состоит в выпадении «1» на грани первого кубика, а СС
состоит в выпадении «1» на грани первого кубика, а СС  - в выпадении «1» на грани второго кубика.
- в выпадении «1» на грани второго кубика.
|
|
|
Оп. СС называют несовместимыми, если они не могут произойти в одном испытании. Произведение несовместимых СС 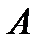 и
и  равно невозможному событию:
равно невозможному событию: 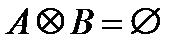 .
.
Пример. Несовместимы при однократном подбрасывании кубика события  .
.
Оп. СС образуют полную группу, если в результате испытания произойдет хотя бы одно из событий этой группы и никакое другое.
Пример. Полная группа для кубика  .
.
Оп. Два несовместимых события  и
и  (не
(не  ) называются противоположными, если они образуют полную группу.
) называются противоположными, если они образуют полную группу.
Пример. Выпадение и не выпадение шестерки при подбрасывании игрального кубика.
Оп. СС будем называть элементарными, если они не могут быть представлены в виде суммы других событий, которые могут произойти в данном испытании.
Пример. При подбрасывании игрального кубика элементарные события:  . СС, состоящее в появлении четного числа очков не является элементарным.
. СС, состоящее в появлении четного числа очков не является элементарным.
Оп. Пространство элементарных событий  - множество, всех элементарных несовместимых СС
- множество, всех элементарных несовместимых СС  , которые могут являться результатом данного испытания.
, которые могут являться результатом данного испытания.  может содержать конечное или даже бесконечное множество элементарных событий. Любое подмножество
может содержать конечное или даже бесконечное множество элементарных событий. Любое подмножество  является СС.
является СС.
Пример. Бросается одна монета, она может упасть гербом  или решкой
или решкой 
 .
.
Пример. Бросаются две монеты:  .
.
Пример. Капля дождя падает на прямоугольную площадку:  .
.
Замечание. В рамках приведенных выше определений достоверное событиепроисходит при проявлении любого элементарного события, то есть содержит их все и обозначается W. Невозможное событие – событие, которое не может произойти в результате данного опыта, оно не содержит элементарных событий и обозначается Æ.
Пример. Для игрального кубика достоверное событие состоит в выпадении числа очков не выше шести при однократном подбрасывании. Невозможное – в выпадении «11» очков при однократном подбрасывании.
События и действия над ними можно наглядно иллюстрировать с помощью диаграмм Венна. Пространство  будем обозначать прямоугольником, элементарное событие – точкой прямоугольника, а каждое событие – подмножеством точек этого прямоугольника. Результат операции над событиями будем заштриховывать.
будем обозначать прямоугольником, элементарное событие – точкой прямоугольника, а каждое событие – подмножеством точек этого прямоугольника. Результат операции над событиями будем заштриховывать.
|
|
|






Первая диаграмма показывает, что сумму двух любых событий можно представить как сумму двух несовместимых событий.
Операции над событиями обладают следующими свойствами:
1.  (переместительный закон)
(переместительный закон)
2. 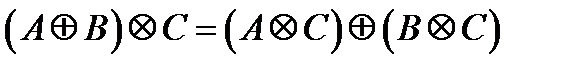 (распределительный закон).
(распределительный закон).
3.  (сочетательный закон)
(сочетательный закон)
4. 
5. 
6. 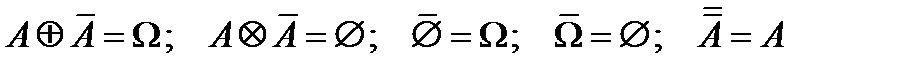
7. 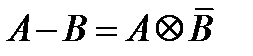
8.  - законы де Моргана
- законы де Моргана
Относительная частота и вероятность события.
Оп. Если в серии из  одинаковых испытаний СС
одинаковых испытаний СС  проявится
проявится  раз, то величина
раз, то величина  называется относительной частотой СС
называется относительной частотой СС  , а
, а  - частотой СС
- частотой СС  .
.
Свойства относительной частоты.
1.  , так как
, так как  .
.
2.  , так как
, так как  .
.
3. Если 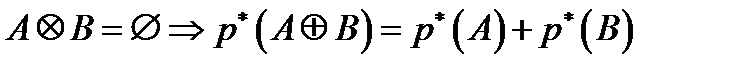 , так как
, так как 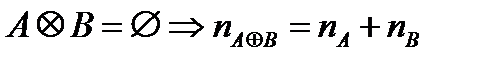 и
и

На начальном этапе развития ТВ проводились эксперименты по непосредственному определению относительной частоты для различных СС. Было установлено, что относительная частота обладает свойством статистической устойчивости: с увеличением числа испытаний она принимает значения, близкие к некоторому постоянному числу.
Оп. (статистическое определение понятия вероятности). Вероятностью проявления СС  в однократном испытании
в однократном испытании  называется число, к которому стремится значение относительной частоты
называется число, к которому стремится значение относительной частоты  при увеличении числа испытаний
при увеличении числа испытаний  :
:  .
.
Замечание 1. Стремление относительной частоты к вероятности нельзя свести к обычному предельному переходу, который рассматривался в математическом анализе.
Замечание 2. Основным недостатком статистического определения понятия вероятности –
необходимость проведения достаточно большой серии испытаний СС.
В теории вероятностей широко используется другое, эквивалентное предыдущему, определение понятия вероятности – классическое определение. Взаимосвязь между статистическим и классическим определением понятия вероятности можно продемонстрировать не примере решения следующей задачи.
Пример. В корзине из  шаров
шаров  черных, Какова вероятность извлечь наугад черный шар при однократном испытании?
черных, Какова вероятность извлечь наугад черный шар при однократном испытании?
Проведем серию достаточно большого количества испытаний, состоящих в извлечении из корзины наугад шара (число испытаний  должно быть настолько большим, чтобы можно было вычислять вероятность СС
должно быть настолько большим, чтобы можно было вычислять вероятность СС  - появления черного шара, по статистическому определению). Будем фиксировать его цвет и возвращать обратно в корзину. При однократном испытании каждый из шаров имеет равные шансы быть извлеченным из корзины. Если число испытаний значительно больше числа шаров и шары неотличимы друг от друга, то можно утверждать, что каждый из шаров будет извлечен одинаковое число
- появления черного шара, по статистическому определению). Будем фиксировать его цвет и возвращать обратно в корзину. При однократном испытании каждый из шаров имеет равные шансы быть извлеченным из корзины. Если число испытаний значительно больше числа шаров и шары неотличимы друг от друга, то можно утверждать, что каждый из шаров будет извлечен одинаковое число  раз. Тогда
раз. Тогда  . И вероятность находится
. И вероятность находится  . С точки зрения однократного испытания, число
. С точки зрения однократного испытания, число  дает число исходов, благоприятствующих проявлению события
дает число исходов, благоприятствующих проявлению события 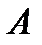 в однократном испытании. А число
в однократном испытании. А число 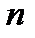 дает число всевозможных, равновозможных и несовместимых исходов однократного испытания события
дает число всевозможных, равновозможных и несовместимых исходов однократного испытания события  .
.
|
|
|
Оп. (классическое определение понятия вероятности). Вероятность наступления СС 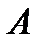 в однократном испытании
в однократном испытании 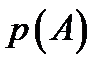 равна отношению числа исходов
равна отношению числа исходов  , благоприятствующих проявлению СС
, благоприятствующих проявлению СС 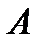 , к числу
, к числу  всевозможных, равновозможных и несовместимых исходов однократного испытания:
всевозможных, равновозможных и несовместимых исходов однократного испытания:  .
.
Свойства вероятности.
1.  , так как
, так как  .
.
2.  , так как
, так как  .
.
3. Если СС  попарно несовместимы, то выполняется равенство
попарно несовместимы, то выполняется равенство  .
.
 На диаграмме Венна СС изображаются не перекрывающимися областями. Число элементарных исходов, благоприятствующих проявлению какого-либо из них равно сумме чисел исходов, благоприятствующих проявлению каждого:
На диаграмме Венна СС изображаются не перекрывающимися областями. Число элементарных исходов, благоприятствующих проявлению какого-либо из них равно сумме чисел исходов, благоприятствующих проявлению каждого:

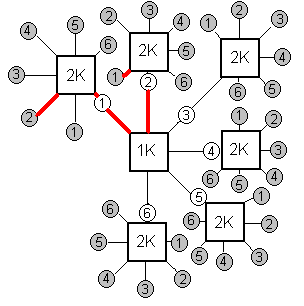
Пример. Однократно подбрасывают два игральных кубика. Какова вероятность, что сумма выпавших очков равна трем?
Рассмотрим решение задачи при помощи составления “ дерева вероятностей ”. Этот способ является наглядным методом перебора всевозможных исходов испытания с целью определения числа всевозможных и благоприятствующих исходов.
На рисунке белыми кружочками выделены всевозможные исходы подбрасывания первого кубика  . Поскольку число очков, выпавших на первом кубике, никак не влияет на число очком, выпавших на втором, то с каждым исходом подбрасывания первого кубика комбинируются все возможные исходы подбрасывания второго (выделены затемненными кружочками). Считая число кружочков после второго кубика, получим число всевозможных исходов испытания
. Поскольку число очков, выпавших на первом кубике, никак не влияет на число очком, выпавших на втором, то с каждым исходом подбрасывания первого кубика комбинируются все возможные исходы подбрасывания второго (выделены затемненными кружочками). Считая число кружочков после второго кубика, получим число всевозможных исходов испытания 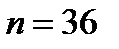 , Жирными линиями выделены пути, приводящие к интересующему нас результату – сумма выпавших очков равна трем. Таких путей два, следовательно
, Жирными линиями выделены пути, приводящие к интересующему нас результату – сумма выпавших очков равна трем. Таких путей два, следовательно  . По классическому определению
. По классическому определению  .
.
|
|
|
Замечание. Классическое определение понятия вероятности неприменимо, если число всевозможных исходов испытания бесконечно; когда нет возможности представить результат испытания в виде совокупности элементарных исходов или нельзя считать эти исходы равновозможными.
Оп. (геометрическое определение понятия вероятности). Пусть задана область  с конечной геометрической мерой
с конечной геометрической мерой  и ее подобласть
и ее подобласть  с конечной геометрической мерой
с конечной геометрической мерой  (в качестве геометрических мер, в зависимости от размерности, могут рассматриваться длина, площадь, объем). Вероятность СС
(в качестве геометрических мер, в зависимости от размерности, могут рассматриваться длина, площадь, объем). Вероятность СС  , состоящего в попадании точки, брошенной наугад в область
, состоящего в попадании точки, брошенной наугад в область  , внутрь ее подобласти
, внутрь ее подобласти  равна отношению геометрических мер:
равна отношению геометрических мер:  .
.
Замечание 1. Выражение “брошено наугад” означает, что вероятность попадания точки в любую подобласть  не зависит от формы или расположения
не зависит от формы или расположения  внутри
внутри  , а зависит лишь от геометрической меры подобласти
, а зависит лишь от геометрической меры подобласти  и пропорциональна этой мере.
и пропорциональна этой мере.
Замечание 2. Можно показать, что все три определения понятия вероятности эквивалентны и приводят к одним и тем же значениям вероятности. Какое из определений использовать при решении конкретной задачи решается из соображений удобства. Классическое определение чаще используется в теории вероятностей, статистическое – в математической статистике. При наличии бесконечного количества исходов используют геометрическое определение.
Элементы комбинаторики.
Подсчет числа всевозможных и благоприятствующих исходов данного испытания простым перебором различных исходов испытания, при большом их количестве, становится непродуктивным. Для нахождения  ,
,  и последующего использования классического определения можно использовать формулы комбинаторики.
и последующего использования классического определения можно использовать формулы комбинаторики.
Оп. Комбинаторика – раздел высшей математики, в котором решаются задачи выбора элементов, обладающих заданными свойствами, из некоторого множества и расположения их в определенном порядке.
Оп. Кортежем длины  , составленным из элементов множеств
, составленным из элементов множеств  , называется конечная последовательность
, называется конечная последовательность  .
.
Замечание. Кортежи, отличающиеся порядком следования элементов – различны. Координаты кортежа  могут повторяться.
могут повторяться.
Пример. Из множеств  и
и  можно составить шесть кортежей длины равной двум.
можно составить шесть кортежей длины равной двум.
 .
.
Оп. Декартовым произведением множеств  называют множество, состоящее из всех кортежей вида
называют множество, состоящее из всех кортежей вида  , и обозначают
, и обозначают  .
.
|
|
|
Пример. Декартово произведение множеств  и
и  равно
равно

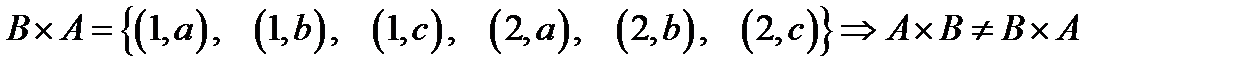
Замечание. Если хотя бы одно из множеств 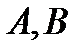 пусто, то их декартово произведение пусто.
пусто, то их декартово произведение пусто.
Правила комбинаторики.
Т. (правило суммы). Если конечные множества 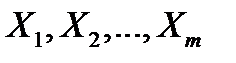 попарно не пересекаются
попарно не пересекаются  , то число элементов в объединении множеств
, то число элементов в объединении множеств 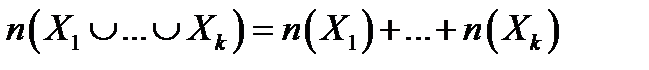 равно сумме чисел элементов соответствующих множеств.
равно сумме чисел элементов соответствующих множеств.
В качестве примера использования правила суммы см. третье свойство относительной частоты и вероятности.
Т. (правило произведения). Если множества 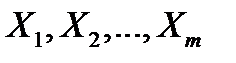 конечны, то число элементов их декартова произведения
конечны, то число элементов их декартова произведения  равно произведению чисел элементов этих множеств.
равно произведению чисел элементов этих множеств.
Пример. В задаче на построение “дерева вероятностей” число  может быть найдено, как декартово произведение множества
может быть найдено, как декартово произведение множества  - исходов подбрасывания первого кубика на множество
- исходов подбрасывания первого кубика на множество  - исходов подбрасывания второго кубика. Исход испытания – это кортеж из элементов этих множеств. Все кортежи этих множеств образуют их декартово произведение. Число таких кортежей находится по правилу произведения равно:
- исходов подбрасывания второго кубика. Исход испытания – это кортеж из элементов этих множеств. Все кортежи этих множеств образуют их декартово произведение. Число таких кортежей находится по правилу произведения равно:  .
.
Пример. Сколько номеров, состоящих из двух букв и идущих за ними трех цифр можно составить, используя 32 букв русского алфавита и 10 цифр?
Множество букв обозначим через  , а множество цифр обозначим через
, а множество цифр обозначим через  . Каждый номер требуемого вида является кортежем, составленным из элементов множеств
. Каждый номер требуемого вида является кортежем, составленным из элементов множеств  . Все кортежи из элементов данных множеств образуют их декартово произведение. Число таких кортежей равно:
. Все кортежи из элементов данных множеств образуют их декартово произведение. Число таких кортежей равно:
 .
.
Формулы комбинаторики.
Размещения.
Оп. Упорядоченным называют подмножество в котором важен порядок следования элементов. В противном случае подмножество называют неупорядоченным.
Пусть задано множество  , содержащее
, содержащее  элементов. Сколько упорядоченных подмножеств, по
элементов. Сколько упорядоченных подмножеств, по  элементов в каждом, можно составить из элементов множества
элементов в каждом, можно составить из элементов множества  , если допустимо (не допустимо) повторение элементов в подмножествах?
, если допустимо (не допустимо) повторение элементов в подмножествах?
Оп. Упорядоченные подмножества, по  элементов в каждом, составленные из множества, содержащего
элементов в каждом, составленные из множества, содержащего  элементов, называют размещениями. Размещения бывают с повторениями (если допустимо неоднократно выбирать один и тот же элемент в подмножество) или размещениями без повторений (если элемент выбирается один раз). Число размещений с повторениями обозначают
элементов, называют размещениями. Размещения бывают с повторениями (если допустимо неоднократно выбирать один и тот же элемент в подмножество) или размещениями без повторений (если элемент выбирается один раз). Число размещений с повторениями обозначают  ; без повторения -
; без повторения - 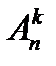 .
.
 Если возможно повторение элементов, то искомое подмножество является кортежем, составленным из элементов множеств
Если возможно повторение элементов, то искомое подмножество является кортежем, составленным из элементов множеств  . По теореме 2 число таких кортежей
. По теореме 2 число таких кортежей  .
.
Если повторение элементов исключено, то каждый элемент из множества 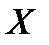 выбирается один раз. Тогда искомое подмножество представляет собой кортеж на множествах
выбирается один раз. Тогда искомое подмножество представляет собой кортеж на множествах  . По теореме 2 число таких кортежей
. По теореме 2 число таких кортежей 
 .
.
Пример. В ящике пять жетонов с буквами  . Из него четыре раза извлекают жетон, который после записи буквы возвращают обратно. Какова вероятность, что ни одна буква не повторится дважды?
. Из него четыре раза извлекают жетон, который после записи буквы возвращают обратно. Какова вероятность, что ни одна буква не повторится дважды?
 .
.
Формула отображения множеств.
Оп. Соответствие, сопоставляющее каждому элементу  множества
множества  один элемент
один элемент  множества
множества  , называется отображением множества
, называется отображением множества  во множество
во множество  :
:  .
.
Найдем число отображений множества 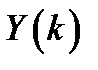 во множество
во множество 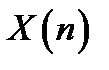 . Каждому отображению множества
. Каждому отображению множества  во множество
во множество  соответствует кортеж длины
соответствует кортеж длины  , составленный из элементов множеств
, составленный из элементов множеств  . Значит, число искомых отображений равно числу таких кортежей, то есть, по правилу произведения равно
. Значит, число искомых отображений равно числу таких кортежей, то есть, по правилу произведения равно  .
.
Пример. Шесть различных конфет между тремя детьми можно разделить  способами. Так как каждой конфете соответствует только один ребенок (конфеты делить нельзя), то множество конфет отображается на множество детей (а каждому ребенку может соответствовать несколько конфет).
способами. Так как каждой конфете соответствует только один ребенок (конфеты делить нельзя), то множество конфет отображается на множество детей (а каждому ребенку может соответствовать несколько конфет).
Перестановки без повторения элементов.
Оп. Определенный порядок следования элементов (упорядочивание), заданный на множестве  называют его перестановкой.
называют его перестановкой.
Если из множества  образуется подмножество, содержащее
образуется подмножество, содержащее 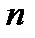 элементов, и при этом не допускается повторение элементов, то от основного множества такое подмножество отличает только порядок следования элементов. Число таких различных подмножеств обозначают
элементов, и при этом не допускается повторение элементов, то от основного множества такое подмножество отличает только порядок следования элементов. Число таких различных подмножеств обозначают 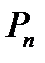 .
.
Оп. Перестановкой без повторения из  элементов называют число размещений
элементов называют число размещений  .
.
Пример. Шесть человек могут сесть на шесть стульев  способами.
способами.
Пример. В корзине 5 одинаковых, занумерованных шаров. По одному, наугад извлекают все шары. Какова вероятность, что их номера появятся в возрастающем порядке.
Исходом испытания по извлечению шаров является перестановка множества из пяти элементов без повторений. Число таких перестановок -  . Благоприятствует одна -
. Благоприятствует одна -  .
.
 .
.
Сочетания без повторений элементов.
Оп. Неупорядоченные подмножества, по  элементов в каждом, составленные из множества, содержащего
элементов в каждом, составленные из множества, содержащего  элементов, называют сочетаниями. Если повторение элементов в подмножествах недопустимо, то число таких подмножеств обозначают
элементов, называют сочетаниями. Если повторение элементов в подмножествах недопустимо, то число таких подмножеств обозначают  .
.
Из множества  мы можем образовать
мы можем образовать  неупорядоченных подмножеств без повторения элементов. Каждое такое подмножество мы можем упорядочить
неупорядоченных подмножеств без повторения элементов. Каждое такое подмножество мы можем упорядочить  способами. В результате получим
способами. В результате получим  упорядоченных подмножеств.
упорядоченных подмножеств.
 .
.
Пример. В студенческой группе двадцать человек – шесть юношей и четырнадцать девушек. На некоторое мероприятие случайным образом выбирают группу из пяти человек. Какова вероятность, что в группе будут трое юношей и две девушки?
При испытании осуществляется выбор подмножества, содержащего пять элементов из основного множества, содержащего двадцать элементов. В данном случае не важно, каким по счету был выбран данный человек – важно, что он попал в группу. Следовательно, подмножества неупорядоченные. Общее число таких подмножеств равно  . Трех юношей выбираем из имеющихся шести, число подмножеств равно
. Трех юношей выбираем из имеющихся шести, число подмножеств равно  . Каждое из таких подмножеств будем рассматривать как элемент множества M(
. Каждое из таких подмножеств будем рассматривать как элемент множества M( ). Число аналогичных выборов девушек -
). Число аналогичных выборов девушек -  . Каждое из таких подмножеств будем рассматривать как элемент множества F(
. Каждое из таких подмножеств будем рассматривать как элемент множества F( ). Благоприятствующий результат выбора студентов есть кортеж на множествах M и F. По теореме 2 – общее число благоприятствующих исходов (кортежей) находится как
). Благоприятствующий результат выбора студентов есть кортеж на множествах M и F. По теореме 2 – общее число благоприятствующих исходов (кортежей) находится как  .
.
 .
.
Пример. В партии из  деталей имеется
деталей имеется  стандартных. Наугад отобраны
стандартных. Наугад отобраны  деталей. Найти вероятность того, что среди отобранных деталей ровно
деталей. Найти вероятность того, что среди отобранных деталей ровно 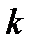 стандартных.
стандартных.
 .
.
Перестановки с повторениями элементов.
Оп. Пусть имеется набор элементов  , в который элемент
, в который элемент  входит
входит  раз; элемент
раз; элемент  входит
входит  раз и так далее. Можно говорить, что задан набор элементов состава
раз и так далее. Можно говорить, что задан набор элементов состава  . Упорядочивание элементов такого набора называют перестановкой с повторениями. Число таких перестановок обозначают-
. Упорядочивание элементов такого набора называют перестановкой с повторениями. Число таких перестановок обозначают-  .
.
Если бы все элементы набора были бы различны, то  .
.
Наличие  одинаковых элементов уменьшает число различных перестановок в
одинаковых элементов уменьшает число различных перестановок в  раз, так как перестановки одинаковых элементов не меняют общего порядка в наборе.
раз, так как перестановки одинаковых элементов не меняют общего порядка в наборе.
 . Нетрудно убедится, что
. Нетрудно убедится, что  .
.
Пример. Переставляя буквы в слове «математика» можно получить  различных порядков следования букв.
различных порядков следования букв.
Пример. Сколькими способами можно разложить двадцать восемь различных предметов по четырем различным ящикам так, чтобы в каждом ящике было по семь предметов.
Числовую ось между числами один и двадцать восемь разделим на четыре равных отрезка – «ящика»  . Число различных перестановок на отрезке
. Число различных перестановок на отрезке 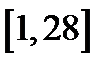 равно
равно  . Но перестановки внутри каждого из четырех отрезков не влияют на состав каждого из четырех ящиков и общее число исходов уменьшается на величину
. Но перестановки внутри каждого из четырех отрезков не влияют на состав каждого из четырех ящиков и общее число исходов уменьшается на величину  .
.
Если ящики одинаковы, то полученный результат уменьшается в число раз, равное числу перестановок ящиков -  .
.
Сочетания с повторением элементов.
Оп. Пусть имеются элементы 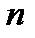 видов, и из них составляется набор, содержащий
видов, и из них составляется набор, содержащий  элементов. Два таких набора считаются одинаковыми, если они имеют одинаковый состав
элементов. Два таких набора считаются одинаковыми, если они имеют одинаковый состав  . Такие наборы элементов назовем сочетаниями с повторениями из
. Такие наборы элементов назовем сочетаниями с повторениями из  элементов по
элементов по  . Число различных сочетаний с повторениями из
. Число различных сочетаний с повторениями из  элементов по
элементов по  обозначается
обозначается  .
.
 Каждый сочетание имеет состав
Каждый сочетание имеет состав  . Закодируем состав, ставя вместо каждого числа
. Закодируем состав, ставя вместо каждого числа  соответствующее количество единиц, а вместо запятых – нули. Число нулей составит
соответствующее количество единиц, а вместо запятых – нули. Число нулей составит  . Находя различные перестановки нулей и единиц (перестановки набора элементов состава
. Находя различные перестановки нулей и единиц (перестановки набора элементов состава 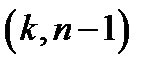 ), будем находить различные составы набора элементов длины
), будем находить различные составы набора элементов длины  , для которых
, для которых  .
.
 .
.
Пример. Сколько наборов из семи пирожных можно составить, если в продаже имеются четыре сорта пирожных?
Из основного множества, содержащего сколь угодно много элементов четырех различных видов, собирают различные подмножества по семь элементов в каждом с возможностью присутствия одинаковых пирожных. Число различных подмножеств такого вида дает выражение  .
.
Лекция №2. Алгебра событий.
Алгебра событий. Теорема сложения вероятностей. Теорема умножения вероятностей. Формула полной вероятности. Формула Байеса.
Рассмотренное ранее третье свойство вероятности называется простой теоремой сложения и справедливо для несовместимых СС. Если СС  и
и  совместимы, то справедлива следующая теорема.
совместимы, то справедлива следующая теорема.
Т. (расширенная теорема сложения). Вероятность проявления, хотя одного из двух СС равна сумме их вероятностей без вероятности их совмещения.
 .
.
 Рассмотрим диаграмму Венна, соответствующую сумме совместимых СС.
Рассмотрим диаграмму Венна, соответствующую сумме совместимых СС.

На этой диаграмме можно выделить три непересекающиеся области -  , которые задают несовместимые события. По третьему свойству вероятности мы можем записать систему:
, которые задают несовместимые события. По третьему свойству вероятности мы можем записать систему:
 Из последней формулы получим
Из последней формулы получим  . Подставляя полученное равенство в первое уравнение системы, получим искомую формулу
. Подставляя полученное равенство в первое уравнение системы, получим искомую формулу  .
.
Замечание. Доказанная теорема сводит нахождение вероятности суммы СС к определению вероятности их произведения.
Следствие 1. Вероятность суммы  СС находится по формуле
СС находится по формуле  , где под выражением
, где под выражением  понимаются вероятность всех комбинаций произведений СС
понимаются вероятность всех комбинаций произведений СС  по одному, по два и т.д. до
по одному, по два и т.д. до  сомножителей. В частном случае, при
сомножителей. В частном случае, при  имеем:
имеем:
 .
.
Следствие 2. Для противоположных событий  и
и 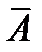 справедливо равенство:
справедливо равенство:  .
.

Зачастую, для нахождения вероятности  удобно использовать формулу
удобно использовать формулу  .
.
Оп. Число, выражающее вероятность СС  , которое найдено при условии, что известен факт проявления СС
, которое найдено при условии, что известен факт проявления СС  -
-  , называется условной вероятностью СС
, называется условной вероятностью СС  и обозначается
и обозначается  или
или  .
.
Т. (расширенная теорема умножения). Вероятность одновременного наступления двух СС  и
и  равна произведению вероятности одного из них на условную вероятность другого:
равна произведению вероятности одного из них на условную вероятность другого:  .
.
 Пусть результатом некоторого испытания могут быть
Пусть результатом некоторого испытания могут быть  равновозможных, несовместимых исходов,
равновозможных, несовместимых исходов,  из которых благоприятствуют СС
из которых благоприятствуют СС  ,
,  - СС
- СС  ,
,  - произведению СС
- произведению СС  .
.

По классическому определению вероятности получим:
 .
.
Следствие. Вероятность одновременного наступления  СС
СС  можно находить по формуле
можно находить по формуле  .
.
Например, для случая совмещения 3-х с.с.:


Оп. CC  и
и  , из одного вероятностного пространства, называются независимыми, если вероятность наступления одного из них не зависит от факта наступления другого:
, из одного вероятностного пространства, называются независимыми, если вероятность наступления одного из них не зависит от факта наступления другого:  .
.
Замечание 1. Последне
|
|
|


