 |
Асимметрия, эксцесс и квантили.
|
|
|
|
Оп. Коэффициентом асимметрии  («скошенности») распределения СВ
(«скошенности») распределения СВ 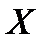 называют величину
называют величину  .
.


Если  , то кривая закона распределения идет более полого правее точки математического ожидания; если
, то кривая закона распределения идет более полого правее точки математического ожидания; если  , то – левее точки математического ожидания.
, то – левее точки математического ожидания.
Оп. Коэффициентом эксцесса  (« островершинности» ) распределения СВ
(« островершинности» ) распределения СВ 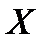 называют величину
называют величину  .
.
Оп. Квантилью уровня  СВ
СВ  называется решение
называется решение 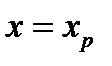 уравнения
уравнения  . Квантили
. Квантили  и
и  имеют специальные названия:
имеют специальные названия:  - нижняя квантиль,
- нижняя квантиль,  - верхняя квантиль,
- верхняя квантиль, 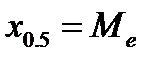 - медиана. Они делят область определения СВ на четыре части, вероятности попадания в которые равны
- медиана. Они делят область определения СВ на четыре части, вероятности попадания в которые равны  .
.
Лекция №11. Непрерывные случайные величины.
Функция распределения случайной величины. Непрерывные случайные величины. Плотность вероятности. Математическое ожидание и дисперсия непрерывной случайной величины. Нормально распределенные случайные величины. Моменты случайных величин.
Плотность распределения вероятностей.
Пусть НСВ  может принимать любые значения из интервала
может принимать любые значения из интервала  , который может быть и бесконечным. Разделим этот интервал произвольным образом точками
, который может быть и бесконечным. Разделим этот интервал произвольным образом точками  на частичные интервалы длины
на частичные интервалы длины  . Пусть известна вероятность попадания значения НСВ
. Пусть известна вероятность попадания значения НСВ  в частичный интервал
в частичный интервал 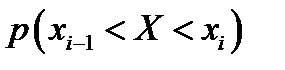 .
.
Оп. Если существует предел  , то функция
, то функция  называется плотностью распределения вероятностей НСВ
называется плотностью распределения вероятностей НСВ  .
.
Замечание. Если вышеописанный предел существует, то, с точностью до бесконечно малой высшего порядка относительно приращения  , справедливо приближенное равенство
, справедливо приближенное равенство  .
.
Т. Вероятность попадания значения НСВ  в интервал
в интервал  равна определенному интегралу от плотности распределения вероятностей
равна определенному интегралу от плотности распределения вероятностей  :
:  .
.


Переходя к пределу при 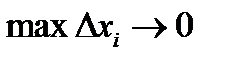 , на основании свойств интегральных сумм получим точное равенство:
, на основании свойств интегральных сумм получим точное равенство:
|
|
|
 .
.
Замечание. Для НСВ, вероятность СС  .
.
 Из приближенного равенства
Из приближенного равенства  следует, что
следует, что 
Свойства плотности распределения вероятностей.
- Если НСВ
 .
. -
 (если все возможные значения НСВ
(если все возможные значения НСВ  ).
). -
 - так как ни на каком интервале вероятность не может быть отрицательной.
- так как ни на каком интервале вероятность не может быть отрицательной.
Замечание. Плотность распределения вероятностей полностью характеризует поведение НСВ и является аналогом закона распределения ДСВ.
Функция распределения.
Определенная для ДСВ функция распределения  может быть использована для описания поведения НСВ:
может быть использована для описания поведения НСВ:  . С геометрической точки зрения значение
. С геометрической точки зрения значение  НСВ равна площади криволинейной трапеции, ограниченной сверху функцией плотности распределения вероятностей, а с права – прямой
НСВ равна площади криволинейной трапеции, ограниченной сверху функцией плотности распределения вероятностей, а с права – прямой  .
.


Свойства функции распределения НСВ аналогичны свойствам функции распределения ДСВ.
-
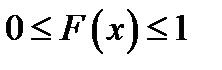 - вытекает из определения функции распределения как вероятности.
- вытекает из определения функции распределения как вероятности. -


-
 - неубывающая функция, то есть из выполнения неравенства
- неубывающая функция, то есть из выполнения неравенства  (см. рисунок).
(см. рисунок).

- Если НСВ

 , то
, то  при
при  и
и  при
при  .
.
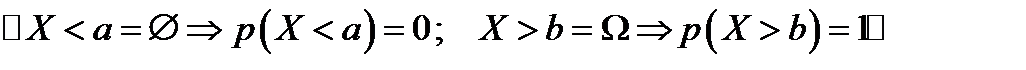
- Если


-
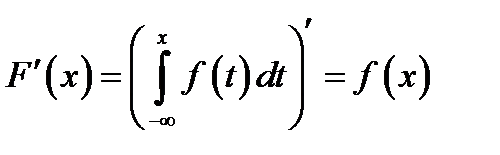 .
.
Числовые характеристики НСВ.
Оп. Теоретическим начальным моментом ( ТНМ )  - го порядка
- го порядка  НСВ
НСВ  называется число
называется число 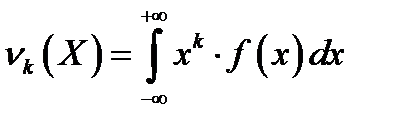 . Теоретическим центральным моментом ( ТЦМ )
. Теоретическим центральным моментом ( ТЦМ )  - го порядка
- го порядка  НСВ
НСВ  называется число
называется число  .
.
Замечание 1. Выписанные формулы можно записать по аналогии с соответствующими соотношениями для ДСВ, если заменить в них дискретные значения ДСВ  их непрерывными аналогами
их непрерывными аналогами 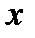 , а вероятности определенных значений ДСВ
, а вероятности определенных значений ДСВ  заменить на элемент вероятности
заменить на элемент вероятности  .
.
Замечание 2. Интегралы в правых частях равенств полагаем абсолютно сходящимися.
Математическое ожидание.
Оп. ТНМ первого порядка НСВ  называется математическим ожиданием НСВ и обозначается
называется математическим ожиданием НСВ и обозначается  .
.
Замечание 1. Как и в случае ДСВ математическое ожидание совпадает со средним наблюдаемым значением СВ по результатам серии достаточно большого количества испытаний.
Замечание 2. Свойства математического ожидания НСВ аналогичны соответствующим свойствам ДСВ.
|
|
|
Замечание 3. Если НСВ  , то
, то
 .
.
Дисперсия.
Оп. ТЦМ второго порядка НСВ  называется дисперсией НСВ и обозначается:
называется дисперсией НСВ и обозначается:  .
.
Замечание 1. Дисперсия НСВ служит мерой разброса значений НСВ вокруг математического ожидания.
Замечание 2. Свойства дисперсии НСВ аналогичны соответствующим свойствам ДСВ.
Замечание 3. Если НСВ  , то
, то  .
.
Замечание 4. Альтернативной мерой разброса для НСВ служит среднее квадратическое отклонение  .
.
Мода и медиана.
Оп. Значение  , при котором
, при котором  НСВ имеет локальный максимум, называется модой.
НСВ имеет локальный максимум, называется модой.
Замечание 1. Если кривая  имеет единственный максимум, то распределение называют унимодальным, если несколько, то – полимодальным.
имеет единственный максимум, то распределение называют унимодальным, если несколько, то – полимодальным.
Оп. Значение  , для которого
, для которого  называется медианой.
называется медианой.
Замечание 1. НСВ  с одинаковой вероятностью может принять значение, лежащее левее и правее медианы плотности распределения.
с одинаковой вероятностью может принять значение, лежащее левее и правее медианы плотности распределения.
Замечание 2. С помощью функции распределения определение медианы можно записать:
 .
.
Пример (равномерное распределение). При измерении величин некоторым прибором, производится округление до ближайшего деления шкалы. Погрешность округления – НСВ  , которая принимает значения
, которая принимает значения  , где
, где  - цена деления шкалы прибора. Найти
- цена деления шкалы прибора. Найти  для НСВ
для НСВ  .
.
Вероятность попадания значения НСВ  в любой интервал
в любой интервал  зависит только от величины
зависит только от величины  , но не от его положения внутри отрезка
, но не от его положения внутри отрезка  . Отсюда следует, что
. Отсюда следует, что  .
.
По второму свойству плотности распределения  . Получим формулу для плотности равномерного распределения
. Получим формулу для плотности равномерного распределения  .
.
Для нахождения  рассмотрим числовую ось, разбитую на три интервала
рассмотрим числовую ось, разбитую на три интервала 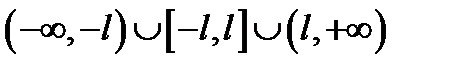 . Пусть
. Пусть  . Рассмотрим следующий интервал
. Рассмотрим следующий интервал
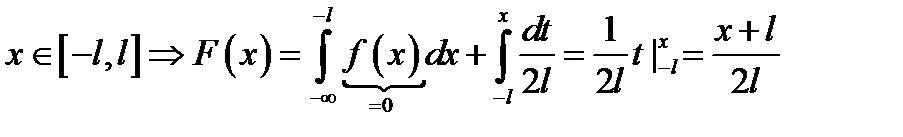 . Для последнего интервала аналогично получим
. Для последнего интервала аналогично получим
 .
.


Найдем числовые характеристики равномерно распределенной НСВ  .
.
 ;
;  ;
;  .
.
Оп. Если во всей области определения НСВ  плотность распределения вероятности этой случайной величины
плотность распределения вероятности этой случайной величины  постоянна, то такое распределение называется равномерным.
постоянна, то такое распределение называется равномерным.
Замечание 1. По аналогии с предыдущим примером, для равномерного распределения можно показать:
 ;
;  ;
;  ;
;  .
.
Замечание 2. Вероятность попадания равномерно распределенной НСВ в заданный интервал  .
.
Замечание 3. ДСВ  также может иметь равномерное распределение, если
также может иметь равномерное распределение, если
 . В этом случае
. В этом случае 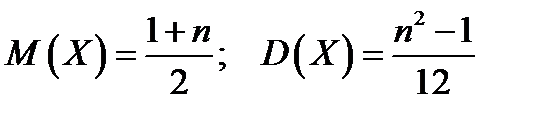 .
.
Нормальное распределение вероятностей ( закон Гаусса ).
|
|
|
Оп. НСВ  распределена по нормальному закону
распределена по нормальному закону  с параметрами
с параметрами  , если, для всех
, если, для всех 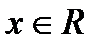 , ее плотность
, ее плотность  .
.


На рисунках приведены графики функции плотности нормального распределения вероятностей и функции распределения при различных значениях параметров. Функция нормального распределения дается интегралом  .
.
Замечание. Если 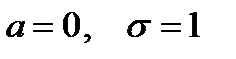 , то такое нормальное распределение
, то такое нормальное распределение  называется стандартным.
называется стандартным.
Свойства функции плотности нормального распределения.
-
 .
. -
 .
. - Функция
 имеет единственный экстремум – максимум в точке
имеет единственный экстремум – максимум в точке
 .
.
- График функции симметричен относительно прямой
 .
. - Точки
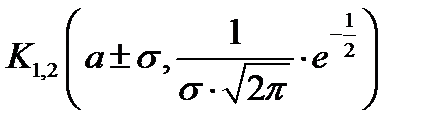 являются точками перегиба функции.
являются точками перегиба функции.
Пример. Доказать, что нормальное распределение удовлетворяет условию нормировки  .
.
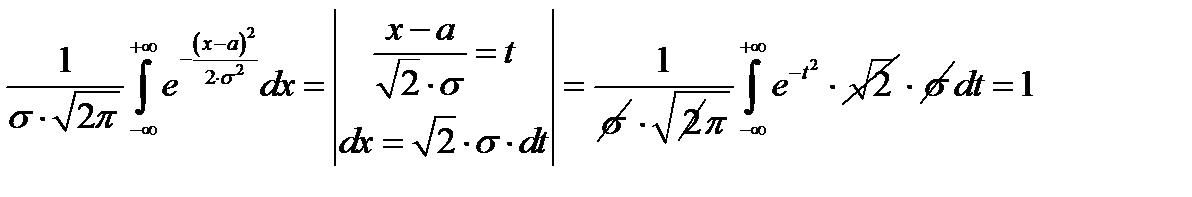 . В доказательстве использован интеграл Эйлера – Пуассона
. В доказательстве использован интеграл Эйлера – Пуассона  .
.
Пример. Найти числовые характеристики  .
.

 .
.
Первый интеграл равен нулю, как интеграл от нечетной функции, взятый в симметричных пределах. Для взятия второго интеграла использован интеграл Эйлера – Пуассона.

 .
.
Замечание 1. В последнем примере показано, что параметры нормального распределения  и
и  дают значения соответственно математического ожидания и среднего квадратического отклонения нормально распределенной НСВ.
дают значения соответственно математического ожидания и среднего квадратического отклонения нормально распределенной НСВ.
Замечание 2. Из симметрии графика функции нормального распределения относительно прямой  следует, что
следует, что  . Можно показать, что
. Можно показать, что  .
.
Найдем вероятность попадания значения НСВ  в интервал
в интервал  . По теореме о вероятности попадания значения НСВ в заданный интервал, получим:
. По теореме о вероятности попадания значения НСВ в заданный интервал, получим:

 .
.
Через интеграл Лапласа выражается и функция распределения НСВ  .
.

Пример. Случайная величина ошибки, при измерении размера детали, подчиняется нормальному распределению с параметром  . Производят четыре независимых измерения. Какова вероятность, что ошибка хотя бы одного измерения не превосходит по модулю величины
. Производят четыре независимых измерения. Какова вероятность, что ошибка хотя бы одного измерения не превосходит по модулю величины  ?
?
За истинное значение размера детали принимают математическое ожидание  НСВ
НСВ  размера детали, которое найдено по данным достаточно большого количества измерений. Тогда, абсолютная величина ошибки измерения равна
размера детали, которое найдено по данным достаточно большого количества измерений. Тогда, абсолютная величина ошибки измерения равна 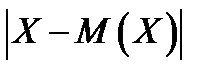 . Вероятность того, что ошибка по абсолютной величине не превысит заданного числа
. Вероятность того, что ошибка по абсолютной величине не превысит заданного числа  , может быть найдена по формуле:
, может быть найдена по формуле:
|
|
|

 .
.
Подставляя в последнюю формулу числовые данные задачи, получим вероятность того, что при одном измерении абсолютная величина ошибки не превысит  .
.
 .
.
Вероятность того, что абсолютная величина ошибки одного измерения превосходит  , составит:
, составит:
 .
.
Вероятность  того, что при всех четырех измерениях абсолютная величина ошибки будет больше величины
того, что при всех четырех измерениях абсолютная величина ошибки будет больше величины  , учитывая независимость измерений, может быть найдена как:
, учитывая независимость измерений, может быть найдена как:
 . По теореме о сумме вероятностей противоположных СС, искомая вероятность равна:
. По теореме о сумме вероятностей противоположных СС, искомая вероятность равна:
 .
.
Полагая в равенстве  , полученном при решении предыдущей задачи,
, полученном при решении предыдущей задачи,  , найдем:
, найдем:  . Этот результат позволяет утверждать, что все возможные значения НСВ
. Этот результат позволяет утверждать, что все возможные значения НСВ  , с достоверностью практически равной единице, лежат внутри интервала
, с достоверностью практически равной единице, лежат внутри интервала  . Сформулированное правило носит название «правила трех сигм».
. Сформулированное правило носит название «правила трех сигм».
Показательное распределение.
Оп. НСВ  распределена по показательному закону с параметром
распределена по показательному закону с параметром 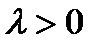 , если ее плотность распределения вероятностей имеет вид:
, если ее плотность распределения вероятностей имеет вид:  .
.
Функцию показательного распределения находим из общей формулы для  . При
. При
 . Для
. Для

 . Получим формулу для функции показательного распределения
. Получим формулу для функции показательного распределения  .
.


Пример. Найти числовые характеристики показательного распределения.
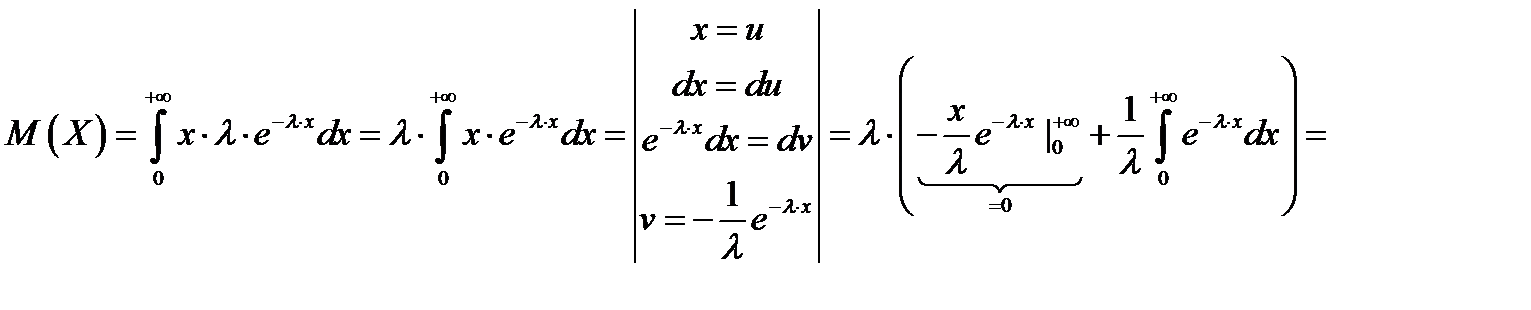
 .
.

 .
.
Пример. Найти вероятность попадания значения показательно распределенной НСВ в заданный интервал.
 .
.
Замечание 1. Показательное распределение используется в физических приложениях, теории надежности, теории систем массового обслуживания. Если, например,  - НСВ длительности безотказной работы устройства. Тогда функция распределения
- НСВ длительности безотказной работы устройства. Тогда функция распределения  определяет вероятность отказа устройства за время
определяет вероятность отказа устройства за время  . А функция
. А функция  определяет время безотказной работы и называется функцией надежности.
определяет время безотказной работы и называется функцией надежности.
Замечание 2. Как и распределение Пуассона, показательное распределение обладает свойством «отсутствия последействия».
|
|
|


