 |
Линии вектора магнитной индукции В всегда замкнуты.
|
|
|
|
Уравнения магнитного поля постоянного тока в интегральной форме
В основе расчета магнитного поля постоянных токов лежит следующая система уравнений в интегральной форме:
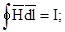
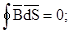
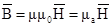
Эту систему следует дополнить выражением объемной плотности энергии магнитного поля
Первый интеграл известен под названием закона полного тока:
циркуляция вектора напряженности магнитного поля равна алгебраической сумме токов, охватываемых контуром интегрирования.
Как известно, положительными считаются токи, направление которых образует правую винтовую систему с направлением обхода по контуру.
Второй интеграл выражает закон непрерывности магнитного потока:
линии вектора магнитной индукции В всегда замкнуты.
Связь между векторами B и H устанавливается третьим уравнением в котором m магнитная проницаемость вещества, а m0 магнитная постоянная. Н измеряется в амперах на метр, а В — в веберах на квадратный метр (в теслах). Следует напомнить, что уравнение, (3.3) применимо только для изотропных сред и является частным случаем соотношения, где вектор намагниченности пропорционален напряженности магнитного поля.
Из выражения удельной энергии магнитного поля (3.4) можно получить формулу для силы dF с которой магнитное поле действует на элемент тока Idl
dF=I[Bdl]
Формулу (3.5) часто рассматривают как уравнение, определяющее вектор В.
Уравнения (3.1) - (3.5) являются основой для расчёта магнитных цепей электромеханических устройств, в том числе и электрических машин.
Уравнения магнитного поля постоянного тока в дифференциальной форме
Уравнения поля в дифференциальной форме так же, как и граничные условия, получаются обычно из уравнений поля в интегральной форме путем предельного перехода к бесконечно малым величинам контура и поверхности интегрирования. Применим к элементарному контуру,
|
|
|
ограничивающему площадку DS, через которую проходит ток DI для точек, где m непрерывно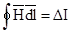 
.
После деления обеих частей этого равенства на DS и перехода к пределу получится
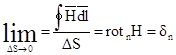
или, учитывая, что проекции векторов равны независимо от
положения контура
.
Это и есть закон полного тока в дифференциальной форме.
Если вихрем вектора напряженности магнитного поля является вектор плотности свободных токов, то вихри вектора магнитной индукции определяются и свободными, и молекулярными токами
.
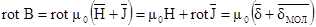Применение уравнения, (3.9) к поверхности элементарной призмы объема DVприводит к выражению
.
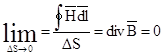Это и есть закон непрерывности линий магнитной индукции в дифференциальной форме.Этот закон свидетельствует о чисто соленоидальном характере поля вектора В: не существует магнитных зарядов, которые служили бы началами и концами для линий магнитной индукции.
Иначе обстоит дело с вектором H. Из выражения
следует, что
,
т.е. концы и начала линий вектора намагниченности являются началами и концами линий H. Так, например линии J начинаются на южном полюсе постоянного магнита и, не выходя за пределы магнита, заканчиваются на северном полюсе. Это и дает повод говорить об имеющих чисто расчетный смысл истоках и стоках вектора H как о “положительных магнитных массах” северного полюса, откуда линии Н направляются вне и внутри магнита к “отрицательным магнитным массам” южного полюса; так как внутри магнита линия H направлены против В, то принято говорить также о размагничивающем действии полюсов.
Граничные условия для векторов магнитного поля
Для точек, лежащих на поверхности раздела двух сред с различными значениями m, уравнения (3.1) и (3.2) при предельном переходе приводят к граничным условиям. Применим закон полного тока (2.1) к контуру элементарного прямоугольника (аналогичного изображенному на рис. 1.3), у которого основание — бесконечно малая первого порядка, высота—бесконечно малая второго порядка, а площадь, следовательно, бесконечно малая третьего порядка. Циркуляция вектора Н сведется к сумме двух слагаемых:
|
|
|
,
а полный ток, равный произведению средней плотности тока (конечной величины) на площадь прямоугольника,— к нулю. Таким образом, искомое граничное условие получается в виде
.
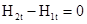Если же применить закон непрерывности магнитного потока (3.2) к поверхности элементарной призмы (аналогичной изображенной на рис. 1.2), у которой площадь боковых граней бесконечно мала по сравнению с площадью оснований, то нетрудно получить граничное условие для нормальных составляющих вёкторов В1n и В2n:
В2n-В1n = 0
Таким образом, в магнитном поле постоянных токов непрерывны, тангенциальные составляющие векторов Н и нормальные составляющие векторов В. Разумеется, Н и Вна границе сред с разными m меняются скачком, чем и обусловлено преломление магнитных линий.
Вектор-потенциал магнитного поля
Пуcть сформулирована следующая задача требуется рассчитать магнитное поле в однородной среде (m), если задано распределение плотности тока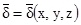 
, иначе говоря, требуется решить систему уравнений '
если плотность тока d задана в виде произвольной функции координат.
Введем новую векторную функцию А =А (х, у, z), позволяющую исключить неизвестные векторы В и Н из уравнений (3.16) и получить взамен их дифференциальное уравнение, решение которого известно.
Такой подстановкой являетcя уравнение
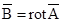
удовлетворяющее требованию div B=0, так как дивергенция ротора тождественно равна нулю. Теперь можно исключить H из первого уравнения (3.16): _
Учитывая, что m = сопst; и что 
получаем
В полученном уравнении можно произвольно задаться значением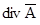 
, не нарушая уравнения.
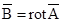
Действительно, если изменять величину дивергенции вектора, то будет меняться только величина потенциальной составляющей этого вектора, ротор от которой равен нулю. В рассматриваемом случае проще всего принять
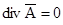
В результате получается векторное уравнение Пуассона
,
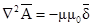а для точек, где d = 0 —векторное уравнение Лапласа
|
|
|
.
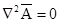Каждое из этих векторных уравнений распадается на три скалярных уравнения:
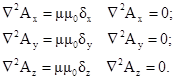
Таким образом, определив А из уравнений (3.22) можно определить магнитную индукцию дифференцированием
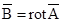
и напряжённость
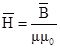
Векторная функция A, с помощью которой решена поставленная задача, называется векторным потенциалом магнитного поля
Если среда состоит из различныхкусочно-однородных (в магнитном отношении областей” то решение системы (3.22) имеет свои особенности, поскольку в этом случае каждая область описывается своим вектор-потенциалом, который надо находить из уравнения Лапласа (если в области нет токов) либо из уравнения Пуассона. Отдельные решения должны удовлетворять граничным условиям (3.14) и (3.15).
Заметим, что граничное условие (3. 14) В1n=B2n удовлетворяется, если A1t=A2t. (это требование достаточное, но не необходнмое). Действительно, нормальная составляющая вектора В есть одновременно нормальная составляющая ротора А. Ноиз структуры дифференциального оператора rot A следует, что его нормальная к поверхности S составляющая определяется изменением вдоль этой поверхности касательных составляющих вектора А. Поэтому, если эти составляющие будут непрерывны, то непрерывны будут также нормальные составляющие rot A и B. В дальнейшем предполагается непрерывность тангенциальных составляющих вектор - потенциала.
|
|
|
