 |
Формула полной вероятности. Формула Байеса
|
|
|
|
Пусть некоторое событие А может произойти вместе с одним из несовместных событий 
, составляющих полную группу событий. Пусть известны вероятности этих событий 
и условные вероятности наступления события А при наступлении события Hi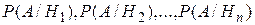 
.
Теорема. Вероятность события А, которое может произойти вместе с одним из событий 
, равна сумме парных произведений вероятностей каждого из этих событий на соответствующие им условные вероятности наступления события А:
 .
| (12) |
Теорема. Вероятность гипотезы после испытания равна произведению вероятности гипотезы до испытания на соответствующую ей условную вероятность события, которое произошло при испытании, деленному на полную вероятность этого события:
 .
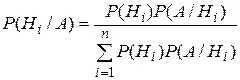| (13) |
Разбор типовых задач
Задача 1
В урну, содержащую 4 шара, опущено 2 белых шара, после чего из нее на удачу извлечен один шар. Найти вероятность того, что извлеченный шар окажется белым, если равновозможны все возможные предположения о первоначальном составе шаров (по цвету).
Решение.
Задача может быть решено с помощью формулы полной вероятности:
,
где 
.
Вероятность события А, которое может наступить лишь при появлении одного из несовместных событий 
, образующих полную группу событий, равна сумме произведений вероятностей каждого их этих событий на соответствующую условную вероятность события А.
В нашем задании событие А – извлечен белый шар;
событие (предположение) 
– первоначально в урне не было белых
шаров;
событие 
– первоначально в урне был один белый шар;
событие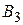 
– первоначально в урне было два белых шара;
событие 
– первоначально в урне было 3 белых шара;
событие 
– первоначально в урне все 4 шара были белые.
|
|
|
Найдем вначале вероятность Р(В i), i = 1 ,…, 5. Т.к. события В 1, В 2, В 3, В 4, В 5равновозможны, несовместны и образуют полную группу, то
;
Пусть 
. Тогда 5 х = 1 
х = 
, т.е. 
, i= 1,…,5.
Для того, чтобы воспользоваться формулой полной вероятности, необходимо найти условные вероятности события А.
Условная вероятность того, что будет извлечен белый шар при наступлении события В 1, есть 
, так как перед извлечением шара число всех шаров в урне (число всех исходов) равно 6, а число белых шаров (число благоприятствующих исходов) равно 2. Аналогично 
, 
, 
, 
. 
Согласно формуле полной вероятности
.
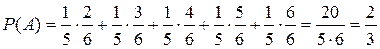Ответ: 
.
Задача 2
В лототрон, содержащий 3 лотерейных билета, добавили пять невыигрышных, после чего извлекли произвольным образом один билет. Какова вероятность того, что он выигрышный?
Решение.
В данном задании А – извлеченный выигрышный билет.
Решаем задачу, как и задачу 1, с помощью формулы полной вероятности.
Запишем полную группу несовместных событий (предположений), при наступлении которых появляется событие А:
событие В 1 – первоначально в барабане выигрышных билетов не было;
событие В 2 – первоначально в барабане был один выигрышный билет;
событие В 3 - первоначально в барабане было два выигрышных билета;
событие В 4 – первоначально в барабане все три билета были выигрышные.
Найдем вероятности Р(Вi), i = 1,2…,4, для чего выпишем систему уравнений, аналогичную системе в задании 1:
.
Пусть Р (В1) = х. Тогда 4 х = 1, откуда 
т.е. 
, i= 1,...,4.
Вычислим условные вероятности события А:
т.к. перед извлечением билета в предположении В 1 число всех билетов (исходов) равно 8, а выигрышных билетов нет. Аналогично:
Согласно формуле полной вероятности:
.
Ответ: 
Нужно заметить, что данный пример можно решить с помощью понятия "противоположные события".
Событие, противоположное событию А, есть 
- извлеченный шар невыигрышный. Если вероятность Р () найдена, то Р (А) = 1- Р ().
|
|
|
Вопросы для самопроверки
1. Что называется событием? Приведите примеры событий.
2. Какие события называются достоверными, невозможными, случайными? Приведите примеры этих событий.
3. Какие события называются несовместимыми? Приведите примеры.
4. Какие события называются совместимыми? Приведите примеры.
5. Какие события называются элементарными? Приведите примеры.
6. Сформулируйте классическое определение вероятности события. Укажите возможные границы вероятности.
7. Что такое относительная частота появления события? В чем состоит свойство устойчивости относительных частот
8. Приведите статистическое определение вероятности.
9. Что понимается под суммой двух событий?
10. Сформулируйте теорему сложения вероятностей для несовместимых событий.
11. Что понимается под полной группой событий? Чему равна сумма вероятностей событий, составляющих полную группу?
12. Какие события называются противоположными? Чему равна сумма вероятностей противоположных событий?
13. Какие события называются зависимыми, независимыми? Приведите примеры зависимых и независимых событий.
14. Что называется условной вероятностью события?
15. Что понимается под произведением двух событий?
16. Сформулируйте теоремы умножения вероятностей для независимых и зависимых событий.
17. Сформулируйте теорему сложения вероятностей для совместимых событий.
18. Приведите формулу полной вероятности.
19. Что понимается под последовательностью из п испытаний?
20. Напишите формулу Бернулли. При решении какого типа задач она применяется?
21. Что такое наивероятнейшее число наступления события при повторных испытаниях? Как вычисляется это число?
22. Сформулируйте локальную теорему Лапласа. При каких условиях она применяется?
23. Напишите формулу Пуассона. При каких условиях она применяется?
24. Напишите формулу для вычисления вероятности отклонения относительной частоты от вероятности появления события в независимых испытаниях.
|
|
|
