Метод эквивалентного генератора

Все рассмотренные методы дают возможность рассчитать токи в цепях с постоянными параметрами. Если же какое-либо сопротивление переменное и нужно определить протекающий по нему ток, то все эти методы будут требовать больших расчетов. Для определения тока в одном изменяющемся сопротивлении применяется метод эквивалентного генератора, основанный на теореме об активном эквивалентном двухполюснике. Эта теорема гласит, что по отношению к выделенной ветви аб всю оставшуюся часть любой сложной цепи можно заменить эквивалентным генератором, ЭДС которого равна напряжению между точками а и б при разомкнутой ветви аб, а внутреннее сопротивление равно сопротивлению пассивной части цепи по отношению к точкам а и б. Эта теорема называется еще и теоремой об эквивалентном генераторе.

Порядок решения задач методом эквивалентного генератора

Для определения тока в заданной ветви аб методом эквивалентного генератора необходимо:

· нарисовать исходную схему без сопротивления в ветви аб;

· в оставшейся части цепи рассчитать токи известными методами;

· найти разность потенциалов между точками а и б (напряжение холостого хода U₀ = U_хх эквивалентного генератора);

· определить внутреннее сопротивление эквивалентного генератора R_вн - сопротивление оставшейся части цепи по отношению к точкам а и б после замыкания всех источников ЭДС накоротко;

· определить искомый ток по формуле

. (1)

Мощность в цепи постоянного тока

Рассмотрим сопротивление, по которому протекает ток. Внутри проводника имеется электрическое поле, которое заставляет электрические заряды двигаться вдоль проводника. Пусть за время t сквозь поперечное сечение проводника прошел заряд q. Так как при протекании тока создается падение напряжения, а напряжение есть работа по перемещению единицы заряда, то

A = qU. (2)

В то же время

P = A / t = (q / t) U = I U,(3)

или

P = IU. (4)

Таким образом, мощность (Р) энергии, выделяемой на сопротивлении, равна произведению тока на напряжение. Заменив ток или напряжение по закону Ома, можно получить и другие формулы для вычисления мощности:

P = I² R, P = U² / R. (5)

Мощность источников вычисляется по формуле:

P = E I, P = J U_J,(6)

где U_J - напряжение на зажимах источника тока, если таковой будет в схеме.

 

Баланс мощностей

При протекании токов по сопротивлениям цепи в последних выделяется тепло. На основании закона сохранения энергии количество теплоты, выделяющейся за единицу времени (мощность) в сопротивлениях цепи, должно равняется энергии, доставляемой за это же время источниками питания.

Уравнение энергетического баланса имеет вид:

å Pист = å Pпотр. (7)

Потенциальная диаграмма

Графической иллюстрацией второго закона Кирхгофа является потенциальная диаграмма (рис. 5), изображающая изменение потенциала вдоль контура, представленного на рис.4. Для построения потенциальной диаграммы необходимо:

1. Заземлить одну точку контура.

2. Произвольно выбрать направление обхода контура.

3. По оси абсцисс отложить в масштабе сопротивления контура в том порядке, в котором они встречаются в направлении обхода.

4. Отложить потенциалы на концах сопротивлений и соединить полученные точки.

2 R1 I1 1 I2 R2 E1 I 3 3 0 E 3 4 R3

j 3

I₃R₃

1 I₂R₂ 4

E₁ I₁R₁ E₃

R

0 0

R₁ R₂ R₃

Рис. 4 Рис. 5

 

Пример 1

На рис.6 представлена расчетная схема. Зададимся направлениями токов, определим независимые контуры и направления обхода. Здесь 6 ветвей с неизвестными токами, 4 узла. Запишем уравнения по законам Кирхгофа:

 

I₁ R₁ 1 R₂

I₁₁ I₃ R₃ I₂₂ E₂

2 R₄ E₄ 3 E₅ R₅ I₂

I₄ I₃₃ I₅ 4

R₆ E₆ I₆

Рис. 6.

I₁ = I₃ + I₂ ,

I₁ = I₆ + I₄ ,

I₂ = I₅ + I₆ ,

I₁ R₁ + I₃ R₃ + I₄ R₄ = E₄ ,

I₃ R₃ - I₅ R₅ – I₂ R₂ = E₂ – E₅ ,

I₄ R₄ - I₆ R₆ + I₅ R₅= E₄ + E₅ –E₆ .

 

Уравнения, записанные по методу контурных токов:

I₁₁ (R₁ + R₃ + R₄) + I₂₂ R₃ + I₃₃ R₄ = E₄ ,

I₂₂ (R₂ + R₃ + R₅) + I₁₁ R₃ - I₃₃ R₅ = E₂ - E₅ ,

I₃₃ (R₅ + R₆ + R₄) - I₂₂ R₅ + I₁₁ R₄ = E₄ - E₆ + E₅.
Решение этой системы дает значения контурных токов. При этом, с учетом выбранных положительных направлений токов: I₁ =I₁₁, I₂ = -I₂₂, I₃ = I₁₁ + I₂₂, I₄ = I₁₁ + I₃₃ , I₅ = - I₂₂ + I₃₃ , I₆ = - I₃₃ .

Вычисления ведутся с точностью до 5 %, что предполагает использование 3-х значащих цифр.

Рассмотрим вычисление тока в R₂ методом эквивалентного генератора, для чего перерисуем схему без этого сопротивления (рис.7). В оставшейся части цепи определим токи методом узловых потенциалов. Здесь число узлов уменьшилось, исчезло сразу два узла.

Заземлим узел 3, для оставшихся запишем уравнения по методу узловых потенциалов:

,

 

I₁ R₁

а в

R₃ E₂

1 R₄ E₄ 2 E₅ R₅

I₄ I₅

R₆ E₆ I₆

Рис. 7

Решение полученного уравнения дает значения потенциала узла 2. Для определения напряжения холостого хода не обязательно вычислять все токи. Здесь достаточно определить ток I₁ и I₅ . По закону Ома для участка цепи:

 

 

j₂ + I₁ (R₁ + R₃) = j₁,

I₁ = (j₁ -j₂ ) / (R₁ + R₃),

j₂ - Е₅ - I₅ R₅ +Е₆ - I₆ R₆= 0,

I₅ = (j₂ - Е₂ +E₆) / R₅ +R₆ , (I₆ = I₅).

Напряжение холостого хода так же определяется по закону Ома для участка цепи: j_а –I₁R₃ –E₅ + I₅ R₅ + E₂ = j_в ,

U_{x x}= U_{а в}= j_а - j_в =Е₅ – Е₂ + I₁R₃ - I₅R₅.

Для определения внутреннего сопротивления эквивалентного генератора перерисуем схему без источников (Рис.8,а), имея в виду, что сопротивление источника ЭДС равно нулю, источника тока – бесконечности. Полученная схема не содержит ни последовательного, ни параллельного соединения элементов. Поэтому необходимо произвести преобразование одного из имеющихся треугольников в звезду (рис.8,б), затем вычислить эквивалентное сопротивление генератора (R_вн).

R₁ а

а в

R₃ R₁ R₃

1 R₄ 2 R₅ 31 R₅ 2

R₆ R₆ R₅

а) б)

в

Рис. 8

Ток вычисляется по формуле:

 

МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ЗАДАЧЕ 2

Гармоническим (синусоидальным) называется ток, мгновенное значение которого i (t) изменяется по синусоидальному закону:

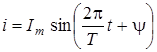(8)

где I_m - максимальное значение, или амплитуда,

- аргумент синуса, или его фаза,

Y - начальная фаза (измеряется в радианах или градусах).

За промежуток времени t = T фаза синусоиды увеличивается на 2p радиан или на 360⁰. Величина, обратная периоду, называется частотой (f =1 / T).

Любой синусоидальной функции можно сопоставить вращающийся вектор (Рис.9). При этом между ними будет однозначное соответствие. Длина вектора равна амплитуде синусоиды, угловая скорость вращения равна угловой частоте. Начальное положение вектора (t = 0) определяется начальной фазой y. При таких условиях проекция вектора на ось ОМ в каждый момент времени равна мгновенному значению ЭДС в тот же момент времени.

М i

w А

A I_m

y

О w t

y

 

 

Рис. 9

Если нескольким синусоидальным величинам сопоставить векторы с соответствующими данными и начальными положениями, то они будут вращаться с одинаковыми скоростями, и их взаимное положение будет оставаться неизменным. Совокупность векторов, изображающих синусоидально изменяющиеся величины с одной и той же частотой, построенных с соблюдением правильной ориентации их относительно друг друга по фазе, называется векторной диаграммой.

Если изменяющиеся величины можно изобразить с помощью векторов, то сами векторы можно записать с помощью комплексных чисел. Как известно, любое комплексное число (а₁ +jа₂) можно изобразить на комплексной плоскости точкой (рис.9). Каждой точке соответствует радиус-вектор (А), проведенный от начала координат. Угол, образованный вектором и вещественной осью, называется аргументом. Он отсчитывается против часовой стрелки. Длина вектора называется модулем, а проекции - действительной и мнимой частями комплексного числа, соответственно. При этом:

А = Ö а₁² + а₂²; a = arctg (a₂ / a₁). (9)

Если проекции выразить через тригонометрические функции

а₁ = A cos a; a₂ = A sin a, (10)

то получим тригонометрическую форму записи комплексного числа:

а₁ + jа₂ = A (cos y +j sin y). (11)

Воспользовавшись формулой Эйлера, можно получить показательную форму записи:

а₁ + ja₂ = A e ^jy, а₁ - ja₂ = A e ^{- jy}. (12)

 

Пусть имеется синусоидальная величина, которая определяется выражением: i = I_m sin(w t + Y). Это выражение соответствует проекции вращающегося вектора I_m на вертикальную ось. С другой стороны, рассмотрим комплексное число.

I_me^jy = I_m cos y + j I_m sin y. (13)

Если положить, что a = w t +Y, то синусоидальной функции будет соответствовать мнимая часть комплексного числа:

i = М. ч. [ I_m e^{j ( w t + Y )}] = M. ч. [ I_m e ^jY e ^{j w t} ], (14)

где М. ч. - сокращенное название “мнимая часть”.

Величину I_m e ^jY = I_m называют комплексной амплитудой. Эта величина является изображением синусоидальной величины, или ее символом. Отсюда название символического метода. Множитель e ^{jw t} называется вращающим множителем. Для всех векторов, вращающихся с одинаковой скоростью, этот множитель одинаков, и в уравнениях обычно его опускают. В комплексной форме можно использовать все методы расчета, полученные для цепей постоянного тока.

Пример 2

Заданы параметры (рис.10) цепи и входное напряжение u=U _msin(wt+y)

 

1 R₁ L₁ 2

I₁

R₂ R ₃

U I₂ I₃

L₂ C₃

3

Рис. 10

Запишем исходные данные в комплексной форме:

U = U e^jy ,

Z ₁= R₁ + jwL₁,

Z ₂= R₂ + jwL₂ ,

Z ₃= R₃ - j 1/wC₃ .

Определим:

· Комплекс полного сопротивления цепи:

· Токи
, , .

· Напряжения на отдельных участках:

U₁₂ = I₁ Z ₁, U₂₃ = I₁ Z ₂₃.

На основании полученных комплексных выражений записываются выражения для мгновенных значений токов и напряжений.

Комплекс полной мощности источника определяется путем умножения комплекса напряжения на сопряженный комплекс тока (сопряженное комплексное число имеет противоположный знак при мнимой части):

.

Комплекс мощности потребителей определяется как

.

+1

 

jwL₁

U R₁I₁

U₂₃ jwL₂ I₂

jwX_c I₃

I₁

R₃ I₃ I₂

I₃

+ j R₂ I₂

Рис. 11

Построение векторной диаграммы (рис.11) начинается с выбора масштаба по току и по напряжению. Их надо выбирать так, чтобы в одном сантиметре (клетке) было число, кратное 2; 2,5; 5; 10. Диаграмму желательно разместить на листе формата основного текста.

 

Сначала строится вектор напряжения U₂₃. Далее строятся векторы токов I₂ , I₃ и их сумма. От начала координат строят векторы напряжений на активных сопротивлениях ветвей (в некоторых вариантах они отсутствуют).

После этого строятся вектора напряжений на реактивных сопротивлениях от концов соответствующих векторов напряжений активных сопротивлений. Они будут, во-первых, взаимно перпендикулярны, во-вторых, их суммы равны U₂₃ . Векторы напряжений на элементах первой ветви строятся от конца вектора U₂₃. При построении векторов рекомендуется пользоваться алгебраической формой записи комплексного числа.

Мгновенное значение мощности определяется как произведение мгновенных значений тока и напряжения:

p = u i = U­_m sin w t I_m sin(w t + j) = U I cos j - U I cos (2 w t - j).

МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ЗАДАЧЕ 3

Электрические цепи зачастую содержат катушки индуктивности, находящиеся пространственно в зоне действия магнитных полей других катушек. При изменении тока в одной катушке в другой возникает ЭДС взаимоиндукции, определяемая по закону электромагнитной индукции. Если цепь второй катушки замкнута, в ней возникает ток, который, в свою очередь, создает свой поток, пронизывающий первую катушку. В том случае, когда эти потоки направлены одинаково, соединение катушек называется согласным, и наоборот.

L₁ M L₂ L1 M L₂

* * * *

i₁ i₂ i₁ i₂

a) б)

Рис. 12

На схемах взаимоиндукцию принято обозначать условно (рис.13). При этом если токи входят в одноименные зажимы (обозначенные звездочкой или иным способом), то включение согласное (рис.13,а), и наоборот (рис.13,б). Очевидно, если в цепи второй катушки нет источника, потоки могут быть направлены только встречно, так как возникающий при этом ток препятствует “...причине, его вызывающей...” (закон Ленца).

Пример 3

Расчеты разветвленных цепей с синусоидальными источниками можно вести, составляя уравнения по законам Кирхгофа или методом контурных токов. При составлении уравнений по законам Кирхгофа нужно задаться положительными направлениями токов и направлением обхода. ЭДС взаимной индукции учитывается как соответствующее падение напряжения. Знак этого напряжения берется с плюсом, если направление обхода контура и ток в индуктивно связанном элементе входят в одноименные зажимы. Для цепи (рис. 13) составим уравнения:

I₁ M I₂

d c * b e * f

R₁ L₁ L₂ R₂

L₃

e₁ I I₃ a II e₂

R₃

Рис. 13

, (15)

, (16)

I₁ + I₂ = I₃. (17)

Решив систему этих уравнений, находим токи в цепи.

Изображение разности потенциалов на комплексной плоскости
и топографическая диаграмма.

Потенциалы точек цепи переменного тока являются комплексными величинами. На плоскости комплексное число можно изобразить либо точкой, координаты которой равны действительной и мнимой частям комплексного потенциала, либо вектором, направленным от начала координат к данной точке плоскости

+j

а i б a U_аб

а)б) j_а j_б б

u_аб +1

Рис. 14

. На рис. 14,а изображен участок электрической цепи, для которой выбрано положительное направление тока и напряжения, совпадающее, как обычно, с направлением тока. Согласно закону Ома для участка цепи можно записать j_a - I_аб Z = j_б, откуда имеем:

j_a - j_б = I_аб Z = U_аб . (18)

На комплексной плоскости потенциалы точек а и б изобразятся векторами j_a и j_б (рис.15,б). Тогда вектор U_аб согласно (18) будет направлен из точки б к точке а, т.е. не так, как на электрической схеме. Так как каждая точка электрической цепи, в которой соединяются сопротивления, имеет свой потенциал, то совокупность векторов, изображающих эти потенциалы на комплексной плоскости будет топографической векторной диаграммой.

 

 

 

 

RI₁ + j

c d

jwMI₂ E₁

 

jwL₁I₁

e R­₂I₂

f

jwMI₁

E₂

jwL₂I₂

b

I₁ jwL₃I₃

R₃I₃

0 a

 

I₂ I₃

 

Рис. 15

 

 

Топографическая диаграмма строится в определенном порядке. Выбирается точка нулевого потенциала, задается положительное направление обхода (рис.13). Затем обозначается каждая точка электрической схемы буквами. Обходя контур по возможности против тока, строят вектора падений напряжений один за другим, начиная с нулевой точки (Рис.15). Чтобы найти напряжение между двумя точками, достаточно на топографической диаграмме соединить их вектором, который и будет являться вектором напряжения.

 

 

⇐ Предыдущая12

Поделиться:

Воспользуйтесь поиском по сайту: