 |
По выполнению контрольной работы
|
|
|
|
Задание 1
В ящике находятся пять одинаковых приборов, причем три из них неработающих. Наудачу достают два прибора. Найти вероятность того, что среди двух извлеченных приборов окажутся:
а) один неработающий прибор;
б) два неработающих прибора;
в) хотя бы один неработающий прибор.
Решение:
а) определим событие А = {один неработающий прибор}.
Число благоприятных для события А исходов равно
m(A) = 3∙2 = 6.
Общее число возможных исходов составит
Тогда Р(А)= 
б) определим событие В = {два неработающих прибора}.
Число благоприятных для события В исходов равно
Общее число исходов 
потому что условия опыта те же.
Тогда 
в) определим событие С = {хотя бы один неработающий прибор}.
В этом случае удобно перейти к дополнительному событию 
= {ни одного неработающего прибора} = {оба работающих прибора}.
Число благоприятных исходов для события равно 
так как только одним способом можно выбрать два работающих прибора из двух работающих.
Число всех исходов n = 10, так как условия опыта остались прежними.
Тогда Р() = 
Для вероятности исходного события С, используя свойства вероятности, получим
Р(С) = 1 – Р() = 1 – 0,1 = 0,9.
Задание 2
В первой коробке 5 красных и 3 зеленых карандаша, а во второй – 3 красных и 4 зеленых. Из первой коробки наудачу достают 3 карандаша, а из второй – 2 карандаша. Найти вероятность того, что среди взятых карандашей будут:
а) все карандаши красного цвета;
б) все карандаши одного цвета.
Решение:
а) определим события:
К = {все карандаши красного цвета};
К1 = {красные карандаши из первой коробки};
К2 = {красные карандаши из второй коробки}.
Событие К наступит, если наступят одновременно события и К1, и К2, т. е. К = К1 ∙ К2.
|
|
|
Так как коробки различные, то события К1 и К2 – независимые. Тогда по теореме умножения получим
Р(К) = Р(К1 ∙ К2) = Р(К1) ∙ Р(К2).
Р(К1) = 
так как все исходы равновозможные.
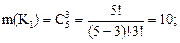
Отсюда Р(К1) =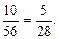 
Аналогично находим
Р(К2) = 
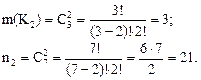
Отсюда Р(К2) = 
Окончательно получаем Р(К) = 
б) определим события:
В = {все карандаши одного цвета};
К = {все карандаши красные};
З = {все карандаши зеленые}.
Событие В наступит, если наступит какое-либо одно из событий К или З, т. е. В = К + З.
А так как события К и З несовместные, то по теореме сложения получим
Р(В) = Р(К + З) = Р(К) + Р(З).
Используя формулу классической вероятности и теорему умножения, получим
Р(З) = Р(З1) ∙ Р(З2),
где З1 = {зеленые карандаши из первой коробки};
З2 = {зеленые карандаши из второй коробки}.
Р(З1) = 
Р(З2) = 
Отсюда, получаем Р(З) = 
Таким образом, с учетом ответа в пункте а) имеем
Р(В) = 
Задание 3
Из коробки, содержащей 25 конфет, среди которых 6 шоколадных, наудачу выбраны три конфеты. Случайная величина Х – число шоколадных конфет среди отобранных. Записать ряд распределения СВ Х, найти функцию распределения F(x) (и построить ее график), математическое ожидание, дисперсию. Построить многоугольник распределения.
Решение
Случайная величина Х – дискретная и принимает значения: 0, 1, 2, 3. Найдем вероятность каждого значения по формуле классической вероятности.
Р(Х = 0) = Р (все три конфеты не шоколадные) = = 
Р(Х = 1) = Р (одна из трех конфет шоколадная) = 
Р(Х = 2) = Р (две конфеты из трех шоколадные) = 
Р(Х = 3) = Р (все три конфеты шоколадные) = 
Ряд распределения СВ Х имеет следующий вид:
| Х | ||||
| Р | 0,42 | 0,45 | 0,12 | 0,01 |
Причем 
Функция распределения имеет вид:
График функции распределения F(x) представлен на рис. 2.
Рис. 2
Многоугольник распределения СВ Х представлен на рис. 3.
Рис. 3
Математическое ожидание СВ Х:
М(Х) = 
= 0 ∙ 0,42 + 1 ∙ 0,45 + 2 ∙ 0,12 + 3 ∙ 0,01 = 0,72.
|
|
|
Дисперсия СВ Х:
D(X) = 
= (0 – 0,72)2 ∙ 0,42 + (1 – 0,72)2 ∙ 0,45 +
+(2 – 0,72)2 ∙ 0,12 + (3 – 0,72)2 ∙ 0,01 = 0,5.
Задание 4
Случайная величина Х имеет нормальное распределение с параметрами m = 11 и σ = 1. Найти вероятность того, что случайная величина Х принимает значения:
а) из интервала [5,13];
б) меньшее 5;
в) большее 13;
г) отличающееся от своего среднего m по абсолютной величине не больше чем на 6.
Решение:
а) вероятность попадания нормально распределенной случайной величины Х в заданный интервал [a, b] определяется формулой:
Р(a ≤ Х ≤ b) = Ф 
– Ф 
где Ф(x) – функция Лапласа.
Отсюда получаем
Р(5 ≤ Х ≤ 13) = Ф 
– Ф 
= Ф(2) – Ф(–6) =
= 0,4772 + 0,4999 = 0,9771;
б) вероятность того, что случайная величина Х принимает значения, меньшие a, определяется формулой
Р(Х < a) = Ф 
+ 
.
Отсюда получаем
Р(Х < 5) = Ф + = Ф(–6) + = –0,4999 + = =0,0001;
в) вероятность того, что случайная величина Х принимает значения, большие b, определяется формулой
Р(Х > b) = – Ф 
Отсюда получаем
Р(Х > 13) = – Ф = – Ф(2) = – 0,4772 = 0,0228;
г) вероятность отклонения случайной величины Х от среднего m не более чем на ε находится по формуле
Р(
< ε) = 2Ф 
Отсюда получаем
Р(
< 6) = 2Ф 
= 2Ф(6) = 2 ∙ 0,4999 = 0,9998.
Задание 5
Задана выборка
2, 0, 2, 0, 3, 2, 1, 4, 3, 5, 3, 1, 1, 2, 3, 2, 1, 2, 2, 1.
По заданной выборке:
а) составить вариационный ряд и статистический закон распределения;
б) построить полигон;
в) составить эмпирическую функцию распределения и построить ее график;
г) вычислить несмещенные оценки среднего значения m, дисперсии σ2 и среднего квадратичного отклонения σ: 
, S2, S;
д) найти доверительный интервал для среднего значения m с доверительной вероятностью γ = 0,8.
Решение:
а) вариационный ряд: 0, 1, 2, 3, 4, 5.
Объем выборки n = 20.
Статистический закон распределения:
| хi | ||||||
| ni | ||||||
| μi | 
| 
| 
| 
| 
|
|
где ni – частота;
μi – относительная частота;
i = 1, 2, …, 6;
б) полигон частот выборки приведен на рис. 4.
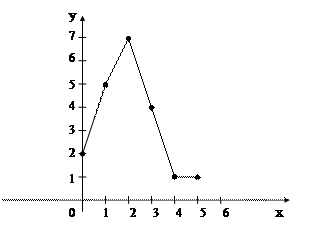
Рис. 4
Изображаем точки с координатами (хi, ni) и соединяем и525122х отрезками;
в) эмпирическая функция распределения F*(х):
При построении графика функции F*(х) откладываем значения в интервале от 0 до 1 (рис. 5);
Рис. 5
|
|
|
г) выборочное среднее 
вычисляем как среднее арифметическое всех выборочных значений
= 
(0 ∙ 2 + 1 ∙ 5 + 2 ∙ 7 + 3 ∙ 4 + 4 ∙ 1 + 5 ∙ 1) = 2.
Несмещенная выборочная дисперсия S2 равна
S2 = 
((0 – 2)2 ∙ 2 + (1 – 2)2 ∙ 5 + (2 – 2)2 ∙ 7 + (3 – 2)2 ∙ 4 +
+ (4 – 2)2 ∙ 1 + (5 – 2)2 ∙ 1) = 
(8 + 5 + 4 + 4 + 9) = 1,58.
Стандартное отклонение S равно
S = 
д) так как объем выборки n = 20, по таблице распределения Стьюдента найдем tα, для α = 1 – γ = 0,2 и k = n – 1 = 19, tα = 1,33.
Доверительный интервал для среднего m вычислим по формуле
Вопросы для самоконтроля
РАЗДЕЛ 1. Вероятность и теоремы о ней
1.1. Что называется случайным событием? Приведите примеры.
1.2. Что называется суммой, разностью, произведением событий?
1.3. Какие события называют: дополнительными, несовместными, независимыми?
1.4. Запишите формулу классической вероятности. Когда применяют эту формулу?
1.5. Сформулируете свойства классической вероятности.
1.6. Запишите формулу полной вероятности. Когда применяют эту формулу?
1.7. Приведите примеры полной группы событий. Какие вероятности находятся по формулам Байеса? Запишите эти формулы.
1.8. Сформулируйте теоремы сложения и умножения вероятностей.
1.9. Запишите формулу Бернулли. Когда она используется? Приведите примеры.
1.10. Когда используют приближенные формулы Пуассона и Муавра-Лапласа? Запишите эти формулы.
РАЗДЕЛ 2. Случайные величины
2.1. Что называется дискретной случайной величиной?
2.2. Запишите формулу закона распределения некоторой дискретной случайной величины.
2.3. Что называется функцией распределения случайной величины? Приведите пример.
2.4. Что характеризуют математическое ожидание, дисперсия и среднее квадратичное отклонение случайной величины? Напишите формулы.
2.5. Сформулируйте свойства математического ожидания и дисперсии.
2.6. Напишите формулу биномиального закона распределения. Приведите примеры.
2.7. Какое распределение называется геометрическим? Приведите пример.
2.8. Какая случайная величина называется непрерывной? Приведите пример.
2.9. Запишите формулы равномерного и нормального законов распределения.
|
|
|
2.10. Приведите примеры случайных величин, имеющих равномерное, нормальное и показательное распределение.
РАЗДЕЛ 3. Математическая статистика
3.1. Что называется вариационным рядом?
3.2. Приведите примеры дискретных и непрерывных вариационных рядов.
3.3. Что такое полигон и гистограмма?
3.4. Назовите основные числовые характеристики вариационных рядов.
3.5. Какие оценки неизвестных параметров распределения называют точечными, интервальными? В каких случаях они используются?
3.6. Запишите формулы вычисления выборочного среднего, выборочной дисперсии, стандартного отклонения.
3.7. Что такое доверительный интервал для среднего значения? Запишите формулу.
3.8. Что такое доверительная вероятность?
Рекомендуемая литература
1. Агапов, Г. И. Задачник по теории вероятностей / Г. И. Агапов. – М.: Высш. шк., 1986.
2. Вентцель, Е. С. Прикладные задачи теории вероятностей / Е. С. Вентцель, Л. А. Овчаров. – М.: Радио и связь, 1983.
3. Герасимович, А. И. Математическая статистика / А. И. Герасимович. – Мн.: Выш. шк., 1983.
4. Гурский, Е. И. Сборник задач по теории вероятностей и математической статистике / Е. И. Гурский. – Мн.: Выш. шк., 1984.
5. Гуcак, А. А. Высшая математика: учеб. пособие для студентов вузов: в 2 т. / А. А. Гуcак. – Мн.: ТетраСистемс, 1998.
6. Лихолетов, И. И. Высшая математика, теория вероятностей и математическая статистика / И. И. Лихолетов. – Мн.: Выш. шк., 1976.
7. Лихолетов, И. И. Руководство к решению задач по высшей математике и математической статистике / И. И. Лихолетов. – Мн.: Выш. шк., 1976.
Содержание
| Предисловие........................................ | |
| 1. Учебная программа................................. | |
| 1.1. Тематический план предмета....................... | |
| 1.2. Содержание предмета............................. | |
| 2. Общие методические указания по выполнению и оформлению контрольной работы.................. | |
| 3. Краткие теоретические сведения..................... | |
| 4. Контрольная работа................................ | |
| 5. Методические рекомендации по выполнению контрольной работы................................ | |
| 6. Вопросы для самоконтроля.......................... | |
| Рекомендуемая литература............................ |
Учебное издание
|
|
|
