 |
Помехоустойчивое кодирование
|
|
|
|
В качестве помехоустойчивого кода выберем код Хемминга. Данный код, как и все блочные коды, можно формировать несложными кодирующими устройствами пассивного типа (требуются лишь типовые устройства, такие как регистры сдвига, сумматоры и умножители, построенные на типовых элементах цифровой техники: ключах, триггерах, и пр.).
Информационные символы представляют собой оптимальный код неравномерной длины. Поэтому применим помехоустойчивое кодирование для каждых трех символов, следующих последовательно, то есть количество информационных символов k = 
nср 
=5.
Минимальное кодовое расстоянием: d = 2. Количество проверочных символов необходимых для того, чтобы минимальное кодовое расстояние линейного кода достигало значения d равно r³2×d-2-log2 d r=1
Длина кодовой комбинации составит n = k + r = 5 + 1 = 6.
Кодовые комбинации будут определяться как
,
где b - вектор-строка информационных символов;
G к - порождающая матрица, приведенная к каноническому виду.
Каноническая матрица G к имеет вид:
Проверим правильность кода, при этом должен получиться нулевой синдром:
Выбор вида модуляции и расчет параметров системы.
Минимальное кодовое расстояние: d = 2
Количество проверочных символов: 
Длина кода:
N = k + r = 3 + 1 = 4
Техническая скорость на выходе помехоустойчивого кодера составит:
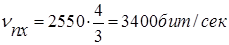
Частота модулирующего колебания определяется информационной скоростью на выходе помехоустойчивого кодера v пх: F = v пх = 3400 Гц.
При выборе вида модуляции нам необходимо учесть следующие условия:
1. Обеспечить вероятность ошибки передачи символа р=7*10-10
2. Полоса канала 25кГц;
3. Передача ведется антенной с круговой диаграммой направленности KU =6дБ на фоне шумов Еш=3 мкВ/м;
|
|
|
4. Максимальная мощность передатчика 200Вт;
5. Дальность действия 110км.
Выбираем частотную модуляцию.
Полоса частот:
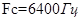
Напряженность поля на входе приемной антенны:
,
где Р - мощность передатчика [Вт];
К - коэффициент усиления антенны [разы];
h 1 - высота подъема передающей антенны [м];
h 2 - высота подъема приемной антенны [м];
r - расстояние между передатчиком и приемником(радиус действия антенны) [м];
При ЧМ отношение сигнал - шум на входе приемной антенны и на выходе демодулятора равны:
Вероятность ошибки:
где Рош.пр. - вероятность ошибочного приема символа;
Ф(ρ) - функция Крампа;
ρ - отношение «сигнал - шум» на выходе демодулятора
При коэффициенте модуляции m=2, заданная вероятность ошибки не выполняется.
Ее можно обеспечить следующими способами: увеличить мощность передатчика, увеличить высоту антенн, на приемной стороне поставить оптимальный различитель или изменить индекс модуляции.
Изменим индекс модуляции. При m=3:
,
При коэффициенте модуляции m=3, заданная вероятность ошибки не выполняется.
При m=4:
Т.е.в этом случае получили необходимую вероятность ошибки.
При этом ошибка декодирования:
,
где q и - количество исправляемых ошибок линейным блочным двоичным кодом;
- биномиальный коэффициент, равный числу различных сочетаний ν ошибок в блоке длинной n;
n - длина кодовой комбинации;
ν - количество ошибок в коде;
Рош. пр. - вероятность ошибочного приема.
Заключение
Проделав данный курсовой проект, мною были изучены основные принципы построения и расчета систем передачи цифровой информации. А именно согласно заданию проведен выбор типа оптимального кодирования и помехоустойчивого кодирования, выбор вида модуляции в канале связи, расчет вероятности ошибки символа при передаче сообщения.
|
|
|
Таким образом, в разработанной системе передаваемая информация имеет набор из 20 сообщений X=0..19, имеющих закон распределения Релея, со скоростью передачи 850 бод с параметрами М=13, D=3. Для передачи этих сообщений по радиоканалу они подвергаются оптимальному кодированию. При оптимальном кодировании используется код Хаффмана. В системе используется частотная модуляция причем полоса модулированного сигнала 6400Гц, которая дает возможность уместить передаваемые сообщения в канал 25кГц. В результате рассчитанная в системе помехоустойчивое кодирование позволяет уменьшить вероятность ошибки символа до p=4,352·10-13, что меньше заданной Р0 = 7 ·10-12
Список литературы
1. Бронштейн И.Н., Семендяев К.А. Справочник по математике для инженеров и учащихся ВТУЗов. - Москва: “Наука”, 1980.
. Вентцель Е.С. Теория вероятностей. - Москва: “Наука”, 1964.
. Дмитриев В.И. Прикладная теория информации. - Москва: “Высшая школа”, 1989.
. Красюк Н.П., Дымович Н.Д. Электродинамика и распространение радиоволн. - Москва: “Высшая школа”, 1974.
. Кудрявцев В.А.,Демидович Б.П. Краткий курс высшей математики. - Москва: “Наука”, 1985.
. Теория электрической связи. Под ред. Д.Д. Кловского. - Москва: “Радио и связь”, 1998.
|
|
|
